Somme de l'énergie

[yy527]

Bonjour

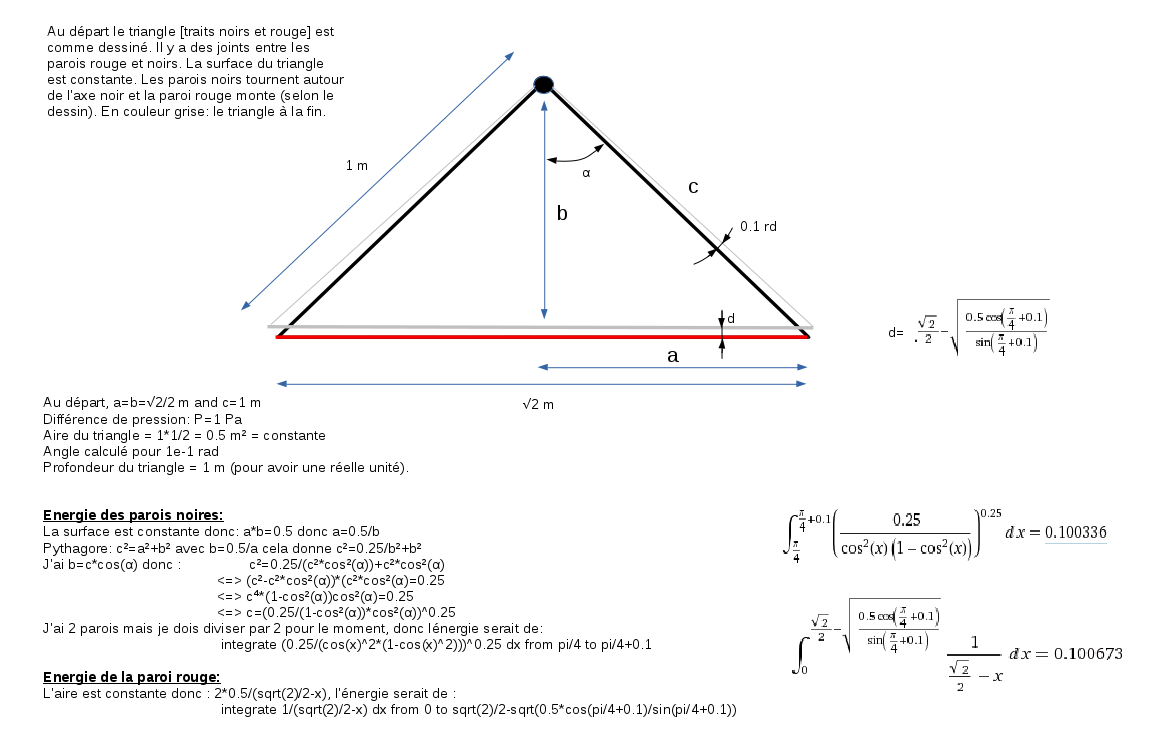
J'ai essayé de calculer la somme de l'énergie lorsque je modifie la forme d'un triangle. Le triangle contient un gaz sous pression: il y a une différence de pression entre l'extérieur et l'intérieur donc une force existe sur chaque paroi du triangle. Je tourne les parois noires autour de l'axe noir, cela me fournit une énergie et je déplace la paroi rouge vers le haut, cela me demande une énergie. C'est un exercice théorique, je n'ai pas tenu compte de la masse ni des frottement mais je pense que je devrai obtenir la même énergie. Si vous voyez mon erreur ? La différence est minime mais j'ai calculé avec wxmaxima et Wolfram et j'ai bien le même résultat.

J'ai tout résumé sur l'image:



a+
-----

[yy527]

Bonsoir,

Personne ne comprend ? dites moi si c'est pas clair SVP. J'ai essayé de détailler un maximum mais ça suffit peut être pas.

Merci

[Dynamix]

Salut

J'ai essayé de calculer la somme de l'énergie lorsque je modifie la forme d'un triangle.

Vu que le volume ne varie pas , elle est aussi nulle que ton problème à la grouille qui n' a pas beaucoup ému la Futura-sphère

[yy527]

Hello

Oui, le volume ne varie pas et et la somme doit être à zéro mais j'ai calculé et je ne trouve pas mon erreur, c'est un chouille presque pareil mais c'est pas une erreur de précision, je pense que mon intégrale concernant les bras noirs n'est pas bonne.
Vu que tu es un expert en problème à la grouille, tu pourrais m'aider à trouver mon erreur ? C'est hyper simple comme grouille: je change juste la forme d'un triangle en gardant constant le volume. Je l'ai pas écrit mais comme tout est instable et que les parois sont indépendantes, il est nécessaire qu'un système externe contrôle les mouvements.

a+

[A voir en vidéo sur Futura]

[invite07941352]

Bonjour,
Ce qui me paraît difficile à trouver , c'est la relation géométrique dans le triangle ,
pour que la surface reste constante si l'on ouvre l'angle au sommet ...
Les barres noires sont de longueur fixe ? Alors la barre rouge s'allonge ...
Et quand l'angle au sommet est 180° , la surface est nulle ...
Et d'ailleurs , cette surface ne diminue t elle pas de façon continue ?

[yy527]

Et quand l'angle au sommet est 180° , la surface est nulle ...

Je calcule juste pour un angle de 0.1 rd (bras noirs) à partir de la position dessinée, effectivement le mouvement n'est pas infini

Les barres noires sont de longueur fixe ? Alors la barre rouge s'allonge ...

Oui, les longueurs des parois changent, c'est un exercice théorique mais on peut imaginer un allongement des parois en pratique

Ce qui me paraît difficile à trouver , c'est la relation géométrique dans le triangle ,
pour que la surface reste constante si l'on ouvre l'angle au sommet ...

J'ai donné les équations, cela fonctionne pour un angle de 0.1 rd ou un peu plus, j'ai calculé pour plusieurs valeurs entre la position dessinée et 0.1 rd (brad noirs) et cela fonctionne bien, il faut juste ne pas remonter trop vite/lentement la paroi rouge

[Dynamix]

En fait , tu calcules un travail :
T = p.S.x
Avec S = c*1 , jusque là , ça va .
Après tu montre directement une intégrale sortie comme par magie d' un chapeau .
Moi , j' ais la flemme d' aller voir ce qu' il y a dans ce chapeau .

Tu devrais essayer avec des valeurs différentes de l' angle de départ et/ou avec un débattement plus grand .

[fabang]

Difficile de comprendre l'objet de ce post. Pour information le volume d'un triangle est nul.

[yy527]

@Dynamix: oui je calcule le travail que fournit la rotations des deux parois noires (1° intégrale) et le travail nécessaire pour bouger la paroi rouge. Je regarde ton calcul et te répond. Pour trouver les intégrales, j'ai utiliser les données :



Ce qu'il y a à l'intérieur des intégrales provient des lignes du dessus, mais je vais essayer de développer plus.

@fabang: il y a une profondeur de 1m, je n'ai dessiné qu'un vue en coupe mais c'est bien un objet en 3d

[Dynamix]

Si j' ais bien compris
Dans les deux cas tu as utilisé la formule du travail en translation T = p.S.x
Pour la deuxième , c' est bon vu qu' il s' agit d' une translation .
Mais la première , c' est une rotation ...

[yy527]

Bonjour,

Oui, la première est une rotation, j'ai mis la variable 'x' comme variable indéfinie, c'est vrai que vous préférez donc l'intégrale est:

integrate (0.25/(cos(α)^2*(1-cos(α)^2)))^0.25 dα from pi/4 to pi/4+0.1

C'est pas pour embêter que je fais cela mais le logiciel Wxmaxima est plus simple à utiliser avec 'x' tout comme Wolfram (le site maths) et comme je donne la formule, il n'y a qu'à copier/coller pour vérifier.

Et merci pour ton aide.

a+

[Dynamix]

Oui, la première est une rotation

Donc le travail c' est : force*bras de levier*angle
Et dans ton intégrale on doit voir c²/2

Il est ou le bras de levier ?

[yy527]

Pour la première intégrale, j'ai pris c/2, mais si je prends l'intégrale de c²/2 c'est pire j'obtiens 0.100084 , la première intégrale est donc:



?

[yy527]

C'est correct avec c²/2 , merci !

[Dynamix]

Dommage que tu ne connaisses pas tes formules de trigo
Tu obtiendrais quelque chose de beaucoup plus simple .
1-cos²x = ???
sinx.cosx = ???
Tu n' aimes pas quand c' est simple ?

Moi , j' aurais posé :
2S = a.b = c²sinx.cosx = ...