RR : des mesures aux coordonnées

[ClairEsprit]

Aucun référentiel ni système de coordonnées ne sont postulés au départ. Le but de la démarche est plutôt de construire/faire émerger ces concepts (et d'autres liés comme les transformations de coordonnées) à partir de presque rien, si ce n'est une métrique, et des instruments et méthodes de mesure.

On commencera par un observateur galiléen, qui observera des objets immobiles, puis en mouvement rectiligne uniforme et finalement en mouvement accéléré. On comparera ensuite avec les observations d'autres observateurs de ces mêmes objets notamment des observateurs non galiléens, par exemple en accélération propre constante.

Le défi est d'être le plus minimaliste possible dans les concepts utilisés et dans les hypothèses de travail.
m@ch3

Marrant... j'ai eu exactement cette démarche il y a quelques années et il en a résulté une vingtaine de pages de "divagation".

On se limitera à dire que l'espace-temps dans lequel se trouve l'observateur est de Minkowski (donc plat et muni d'une forme bilinéaire symétrique nommée tenseur métrique)
m@ch3

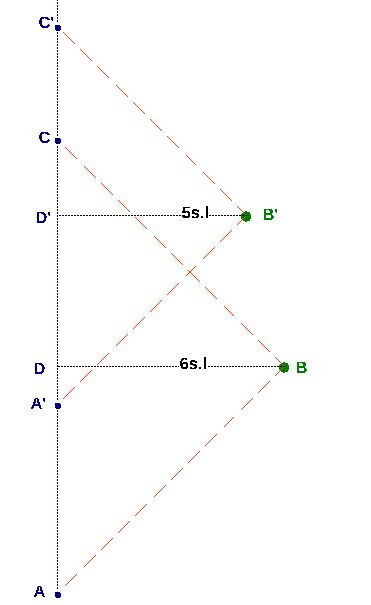
Par contre je n'avais pas supposé ce genre de construction à-priori... mais évidemment, ici, ne pas le faire est hors charte.

Je trouve que vous faites des raccourcis dès que vous parlez d'instrument de mesure existants. Je pense que la démarche doit pouvoir décrire les instruments de mesure, comment les construire et comment mesurer avec. C'est là que ça devient compliqué. La relativité surgit très tôt rien que par le fait d'être obligé d'accepté une invariance à priori (un postulat) des "choses" avec lesquelles on fait des mesures.
-----

[invite6c093f92]

On accepte bien d'autres invariants étant postulés, la durée propre par ex, il faut bien faire "confiance" à un étalon, ici, la longueur c'est l'étalon spatial (local/propre)) et mesurer une distance, c'est déterminer une portion de "trajectoire 4D", (donc n'est plus uniquement spatial de fait...Lapalissade...) en se basant sur un étalon local, qui donne l'unité.
Que l'on choisisse le mètre ou la durée, ce n'est qu'une méthode.
L'important est dans la distinction 3D et 4D, du moins c'est comme ça que je vois ça, je catégorise les mots , j'y mets des concepts différents, je garde la longueur pour le spatial et la distance pour le 4D.
Bref, la longueur-> math pour pouvoir faire des rapports; distance-> Physique pour pouvoir distinguer les événements.
Peut-être que j' ai tord de faire cette distinction, ou la fait mal.

[Zefram Cochrane]

L'observateur ne reste pas au milieu ??

Bonjour,
soit un observateur Bleu accélérant à T=Tb=0s à g°=10m/s² -> Rb=c/g=30 000 000s.l la position de l'observateur à T=0s

posons L = Ro/N et un point P tel que Xp=Ro - L.

Choisisson N=2

A Tb=0s Bleu voit P à Tp=-15 000 000s.

La question est quand et à quelle distance Bleu verra P à Tp=0s.

à Tb=Rb*Sh(Tb'/Rb), Bleu se trouve à Xb=Rb*Ch(Tb'/Rb)

Donc Bleu verra P à Tp=0s si Xb - Tb = Xp -> Rb*[Ch(tb'/rb) - Sh(tb'/Rb)]=Xb -> [Ch(T'b/Rb) - Sh(Tb'/Rb)] = 1/2

De là on déduit la vitesse U=0.6c puis la rapidité u° = Atanh(U) -> Tb'= 20 794 415s = Rb*u°.

T=22 500 000s c'est la distance en s.l parcourue par la lumière pour aller de Xp à Xb.

Comme sa vitesse est U=0.6c, sa perception des distances change: à Xp-Xb lui correspond une distance propre L'= (Xp-Xb)*1/2 = 11 250 000s.l

d'où L'/L=3/4

[mach3]

Bonjour,
soit un observateur Bleu accélérant à T=Tb=0s à g°=10m/s² -> Rb=c/g=30 000 000s.l la position de l'observateur à T=0s

posons L = Ro/N et un point P tel que Xp=Ro - L.

Choisisson N=2 [...]

Pitié, créez un autre fil

Bon, j'essaie de reprendre un peu mes réflexions. On va oublier les règles et mètres rubans pour l'instant et considérer uniquement les mesures par réflexion d'un signal de genre nul.

On prend un observateur galiléen qui fait des mesures de distance successives d'un objet. Considérons deux mesures successives.
On note les évènements suivants :
A : émission par l'observateur du premier signal
B : réflexion du premier signal par l'objet
C : réception par l'observateur du premier signal réfléchi
A : émission par l'observateur du second signal
B : réflexion du second signal par l'objet
C : réception par l'observateur du second signal réfléchi

L'intervalle entre A et A' sera noté (AA'²=), celui entre B et B', t (BB'²=t²), et celui entre C et C', (CC'²=)
L'intervalle entre A et C sera noté 2T (AC²=4T²) et celui entre A' et C' 2T' (A'C'²=4T'²)

On remarque que A, A', C et C' sont tous les 4 sur la ligne d'univers de l'observateur galiléen, qui est une géodésique, donc une droite. On peut considérer un vecteur unitaire de genre temps u tel que
AA'=u
AC=2Tu
CC'=u
A'C'=2T'u

On introduit aussi D et D', les projetés orthogonaux de B et B' sur la ligne d'univers de l'observateur galiléen, avec :
BD² = -T² et B'D'²= -T'²
BD.u=B'D'.u=0
AD=DC=Tu
A'D'=D'C'=T'u

on peut remarquer aussi les relations suivantes, mais je ne suis pas encore certain si elles vont servir ou non (je réfléchi en même temps que je poste et je ne sais pas encore exactement où je vais)
AC²=(AB+BC)²=AB² + BC² + 2AB.BC = 2AB.BC (car AB et BC de genre nul)
et identiquement
A'C'²= 2A'B'.B'C'

Je vais m'intéresser aux relations entre , t et . Mais pas tout de suite parce que malheureusement je dois retourner travailler...

m@ch3

[Zefram Cochrane]

Pas de soucis, je ne faisais que répondre à Nicophil


Ca, c'est que j'ai compris pour le moment.
Les chiffres, ce n'est pas pour donner des longueurs en cm

[Amanuensis]

(...)

Je ne sais pas trop ce que tu cherches à démontrer.

Dans le triangle ADB, on 0 = AB² = AD² + 2 AD.DB - DB² = AD²-DB²

On a donc bien DB² = AD² = AC²/4

Qu'a-t-on besoin de plus? Cela donne la distance et la date de B. Les deux autres coordonnées sphériques sont connues par deux mesures angulaires, B est donc entièrement repéré.

Les mesures successives donneront une série d'événements du mouvement de l'objet...