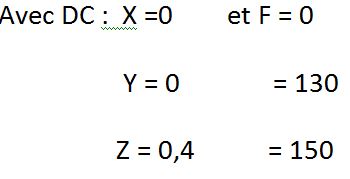Bonjour,
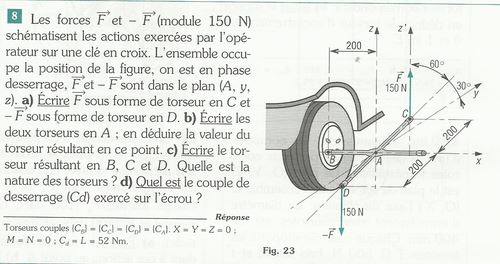
J'essaie de faire cet exo (en pièces jointes) mais n'ayant pas de cours je ne comprends pas comment on trouve les réponses notées en dessous
Est ce que vous pourriez me les expliquer svp ?
Pour la question d, c'est bon, j'ai trouvé le desserrage du couple (CD) = F.d.y = (CD) = 150.0,4.cos(30°) = 52 Nm
Mais les questions a, b et c je ne comprends pas
Je vous remercie
Salut
Tu sais ce qu' est un torseur ?
Quel est le moment de F en C ?
Quelle est la résultante de F ?
Idem pour -F en D
Alors un torseur permet de modéliser une action mécanique d'un solide 1 sur un solide 2.
Le moment de F en C = MD+CD ^S
Avec S (résultante) = 0
Car le torseur couple reste identique en tout points C = 0/M
Est ce que c'est juste ?
Le moment de F en C = (MD) ⃗ + (CD) ⃗ ^ S ⃗
Avec S ⃗ = 0 car seul un moment subsiste, si les 2 forces sont opposées et d’égales intensités et leur résultante est nulle.
Donc Mf→C = (MD) ⃗
Le moment de (-F) ⃗ en D (= MC) ⃗ + (CD) ⃗ ^ S ⃗
Avec S ⃗ = 0 car seul un moment subsiste, si les 2 forces sont opposées et d’égales intensités et leur résultante est nulle.
Donc M-f→D = (MC) ⃗
Ainsi on peut conclure que (Cc)=(Cb)=(Ca)=(Cd) car le torseur couple reste identique en tout points de la clé.
Voilà ce que j'ai compris !
Non .Envoyé par mario64
Un torseur (statique) permet de modéliser l' ensemble des forces qui sont appliquées à un système ou une partie de cet ensemble .
Question A : on te demande le torseur des forces appliquées en C .
Il n' y a qu' une force appliquée en C , c' est F . Donc le torseur de cet ensemble de force ne peut pas être un couple .
C' est un glisseur de moment nul en C .
Le torseur couple c' est le torseur de l' ensemble des forces F et - F .
C' est le torseur résultant de la question B
Ok et vous le notez comment alors la force F en C ?
car la réponse à cette question c'est (Cc)=(Cb)=(Ca)=(Cd) ??
Dsl mais je ne comprend vraiment pas
Les éléments de réduction en C ?
Résultante = F
Moment en C = 0
(Cc)=(Cb)=(Ca)=(Cd) c' est le torseur résultant .
Avant d' en arriver là , il faut , suivant l' énoncé :
_déterminer les élements de réduction de T(F) en C
_déterminer les élements de réduction de T(-F) en D
_Avec la formule que tu connais bien , déterminer les éléments de réduction de T(F) et T(-F) en A
_Additionner les deux pour obtenir T(F,-F) en A
A partir de ce moment seulement , en observant la résultante de T(F,-F), tu peux conclure que c' est un torseur couple , mais pas avant .
ok ! je recommence
a-
Au point C
T(F) = Résultante = F
Moment = 0
Au point D
T(-F) = Résultante = - F
Moment = 0
Au point C et D on est en présence de 2 torseurs glisseurs : car un torseur glisseur est associé à une action mécanique dont le moment est nul en un point.
b-
La résultante des 2 forces F et -F s'annule en ce point : donc Résultante = 0
Hors 2 forces dont la résultante est égale à 0 est un torseur couple. Par conséquent, les éléments de réduction de ce torseur seront les mêmes en tout point de la clé en croix.
Le moment de F en A = CA ^ F
Le moment de -F en A = DA ^ -F
Cb = Cc = Cd = Ca
c-
Le moment de A = moment de B = moment de C = moment de D
Ainsi nous pouvons dire que le T(F; -F) = Résultante = 0
Moment différent de 0 en tout point de la croix
Comme nous sommes en présence d'un torseur couple, les résultantes sont = 0
dont x= 0 - y = 0 - Z = 0
d-
L = -F.d.y
L = -150 . 0,4 . (-cos 30°)
L = 52 Nm
Est ce que c'est juste ? Par contre dans la correction, il est noté M = 0 et N= 0 et je ne sais pas pourquoi
Merci d'avance pour tes conseils
Pour le B , c' est un peu laborieux .
On attend pas de toi un long discours . Tu n' as pas besoin de dire que c' est un couple pour calculer le moment .
Ce qu' on attend dans un exercice sur les torseur , c' est que tu dégaines la formule BABAR . Il faut toujour l' avoir sous le coude dès que tu entend le mot "torseur"
MA(F) = MC(F) + AC Λ F = AC Λ F
Idem pour -F
Ensuite tu peux faire la somme des deux moments , vu que les éléments de réduction sont considérés au même point (A)
Je ne vois pas cette somme dans ton post ? Pourtant c' est demandé dans l' énoncé .
C' est la question C . Il faut terminer le B avant de passer au C .Cb = Cc = Cd = Ca
La nature du torseur (couple) c' est aussi la question C
Trop pressé d' arriver au résultat .Par contre dans la correction, il est noté M = 0 et N= 0 et je ne sais pas pourquoi
M = AB Λ F (ce que tu devrais avoir trouvé à la question B)
Tu connais les composantes x,y,z de AB et de F
Tu effectues le produit vectoriel et tu obtiens les composantes du moment .
Merci pour toutes ces explications !
Par contre pour la question b, on a donc
MA(F) = MC(F) + AC Λ F = AC Λ F
MA(-F) = MD(-F) + AD Λ -F = AD Λ - F
MA (F+/ -F) = AC Λ F + AD Λ - F
MA (F+/ -F) = (0,2 X 1,5) + ( 0,2 x -150)
MA (F+/ -F) = 0
Hors vous me dites que je devrais avoir comme résultat M = AB Λ F ? Pourquoi AB
AD Λ - F = DA Λ F
AC Λ F + AD Λ - F = AC Λ F + DA Λ F = (DA+AC) Λ F = DC Λ F
Erreur de ma part . J' ais écrit AB , mais au lieu de DC
AD est négatif .MA (F+/ -F) = (0,2 X 1,5) + ( 0,2 x -150)
En plus tu as oublié le cos 30
allez je reprends une dernière fois pour la question d
On a donc DC Λ F
Avec DC : X =0 et F = 0
Y = 0 = 130
Z = 0,4 = 150
J’obtiens
L = (0*150) – (0,4*150) = -52
M = (0,4*0) – (150*0) = 0
N = (0*130) – (0*0) = 0
J'applique la méthode du schéma ci dessous
Par contre je trouve L = -52 Nm et non 52 Nm ??
Pardon mes coordonnées se sont décalées
DC = 0/0,4cos30/0,4sin30
F = 0/0/150
