Il serait peut etre temps de te remettre en cause puisqu'on est trois a te soutenir l'inverse. J'ai dit dans premier temps que distance radar = distance propre mais, perso, je me suis vite ravisé. Puisque tu parles de calcul, où est donc celui qui demontre que tu as raison ?Envoyé par Archi3
Trollus vulgaris
Tu as raison la distance propre est de 15s.l. la distance radar de 20.79s.l=41.59/2.
mais par contre la longueur propre ne varie pas entre deux immobiles de Rindler distants et la distance radar ne correspond pas à la longueur propre.
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Purée, c'est bien plus difficile à expliquer que je le croyais (pourtant dans ma tête c'est simple), je dois trouver le bon axe pour une explication claire, et éclairante...
m@ch3
Never feed the troll after midnight!
Pas de problème j'me suis mis en standby. Bon courage
toutes mes excuses (ainsi qu'a Mach3) , c'est moi qui ai tort : effectivement pour les objets distants le temps d'aller retour n'est pas la distance propre * 2/c , ce n'est vrai que pour des objets très proches - en effet la conversion de temps "coordonnées" en "temps propre" n'est pas la même suivant les endroits (à cause de la variation de g_00) . On a bien en coordonnées de Lass ∆x = c ∆t , et donc pour un aller retour, ∆t = 2∆x/c. Mais pour l'expérience "radar", il faut convertir ça en temps propre par g_00 (x1) et écrire, du coup la "distance radar" est
Dernière modification par Archi3 ; 22/11/2017 à 12h10.
Bon, 3e essai pour expliquer cela... j'ai simplifié, c'est dommage parce qu'il y a des aspects du concept de référentiel qu'il aurait été intéressant d'abordé par ce biais, mais je n'arrive pas à en faire un exposé clair et concis, donc ce sera à base de système de coordonnées. Tant pis.Alors voilà... pour obtenir ce que tu dis pour la trajectoire de l'accéléré dans son repère de KM je dois prendre (avec x et t coordonnées en Minko) :
Et ça ne garantit rien sur tout le reste ! Comprend pô...
Merci
Si je pars d'un système de coordonnées de Lorentz (T,X), et que je transforme vers les coordonnées de Rindler, certains mouvements d'accélération propre constante auront une coordonnée spatiale de Rindler constante. Seulement certains mouvements. Ceux dont le "centre" est l'origine du repère de Lorentz considéré au départ (et, "détail", dont l'accélération pointe vers les X positifs). Par "centre d'un mouvement d'accélération propre constante", j'entends l'évènement ayant le même intervalle avec tous les évènements de la ligne d'univers du mouvement (si le centre est O, alors pour tout point M de la ligne d'univers de centre O, OM²=constante, comme le centre d'un cercle en euclidien en somme). Les autres mouvements d'accélération propre constante, de centre différent, ne seront pas à coordonnée spatiale de Rindler constante. Remarquablement, si un mouvement donné est à coordonnée spatiale de Rindler constante, alors le même mouvement mais translaté dans le temps ou dans l'espace n'est pas à coordonnée spatiale de Rindler constante.
Si je pars du même système de coordonnées de Lorentz (T,X) et que je transforme vers les coordonnées de Kottler-Moller, certains mouvement d'accélération propre constante auront une coordonnée spatiale de KM constante. Pas les mêmes que ceux qui avait une coordonnée spatiale de Rindler constante. Au lieu de ceux qui ont l'origine du repère de Lorentz pour centre, c'est ceux qui ont pour centre un évènement situé en (0, -1/g).
On peut par ailleurs, à volonté, inventer des système de coordonnées analogue à Rindler ou à Kottler-Moller, qui font que certains mouvements d'accélération propre constante de centre (T0,X0) dans le repère de Lorentz précédent seront de coordonnées spatiale constante.
Si j'ai un repère de Lorentz quelconque, et que je veux qu'un mouvement d'accélération propre constante g de centre quelconque (T0,X0) soit de coordonnées spatiale constante et de valeur imposée xi, et que sont temps propre coïncide avec le temps coordonnée, alors il y a plusieurs procédures possibles.
L'une d'elle est la suivante :
-on change de repère de Lorentz par une translation spatio-temporelle pour amener (T0,X0) en (0,0)
-on transforme ces nouvelles coordonnées en Rindler
-on effectue une translation spatiale pour amener la coordonnée spatiale 1/g sur xi
remarque : si T0=0, X0=-1/g et xi=0, alors on retrouve Kottler-Moller
Une autre, équivalente :
-on change de repère de Lorentz par une translation spatio-temporelle pour amener (T0,X0) en (0,-1/g)
-on transforme ces nouvelles coordonnées en Kottler-Moller
-on effectue une translation spatiale pour amener la coordonnée spatiale 0 sur xi
remarque : si T0=0, X0=0 et xi=1/g, alors on retrouve Rindler
Après on peut en plus s'amuser à transformer encore les coordonnées spatiales ou temporelles obtenues, avec des logarithme, des exponentielles, ou autre, pour avoir des systèmes plus "exotiques", comme celui de Lass.
m@ch3
Never feed the troll after midnight!
Salut,
Ah ok, en fait KM replace un accéléré de Rindler à l'origine du repere. Chez Minko, si le "centre" est en (0,0) alors l'origine de l'hyperbole est en (1/a,0), il faut replacer le voyageur à l'origine du repere de Minko (trajectoire hyperbolique) puis KM donne le repere dans lequel au moins ce voyageur a une trajectoire verticale et un temps propre regulier (à verifier si le decalage du centre des autres hyperboles vers -1/a en fait aussi des droites) depuis la meme origine (0,0).
A y reflechir... si c'etait le cas j'aurais du le voir puisque j'ai commencé par la trajectoire du voyageur dont j'avais utilisé le parametre 1/a. Dois-je changer directement l'origine de Miko et retrancher 1/a a toutes les valeurs de x avant d'injecter dans les formules Wiki ? Dois conserver les miennes (ce qui revient peut etre au meme...) ? Je vais faire des petits essais pour voir.
Merci pour ton aide
Trollus vulgaris
Salut, j'ai du mal à comprendre parce que dans les coordonnées KM comme dans les coordonées de Lass, et contrairement aux coordonnées de Rindler, c'est le serpent qui se mord la queue
Pour Lass, cette phrase " Une distance radar se mesure par l'aller-retour d'un signal de genre nul d'un observateur vers un évènement (généralement un point de la ligne d'univers d'un objet). Le protocole est simple, l'observateur enclenche son chrono quand il envoie le signal et l'arrête quand il reçoit le signal retour. Il divise la durée en secondes par deux, cela donne la "distance radar" à l'évènement en seconde-lumière." m'a permis de comprendre le schéma : http://forums.futura-sciences.com/ph...ml#post6026613
Pour ma part, je vais me pencher sur les données KM en partant de là :
http://forums.futura-sciences.com/ph...ml#post6030070
et essayer de voir à quoi elles peuvent servir.
Cordialement,
Zefram
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Salut,
A defaut de plancher sur KM j'ai "colorié" le Lass ici http://forums.futura-sciences.com/as...ml#post6033437 (j'ai preferé le mettre là bas parce que j'en ai pas fini avec Rindler et je voudrait que ca soit comparable).
Interessant.. pour info, les courbes grises semblent très proches d'etre une symétrie de la bleue mais ce n'est pas le cas et ce ne sont pas des hyperboles, par contre c'est trois fois la même courbe décalée et on y trouve verticalement un temps propre "proportionnel" (comme d'hab un point = 1s de temps propre y'a qu'à compter). Bleu est toujours l'accéléré à 0,05c/s et le Lass est "son" repère, celui de vert serait exactement le même en deux fois plus petit. L'origine du repère de Lass est au croisement avec l'axe Tau pour la valeur donnée de x' (wiki).
Mais je repose la question, voit on jusqu'à cette distance t x c ? Ou je m'embrouille pour rien ?
Merci
Trollus vulgaris
Et pour insister sur la difference entre longueurs propre et radar : dans le grah en lien la distance propre entre rouge et vert est de 5sl et entre vert et bleu de 10sl. Pourtant, les distances radar sont égales et égales à 13,86sl pour bleu (c'est son repere qui est à l'echelle) et la moitié pour vert etc..
Dernière modification par Mailou75 ; 25/11/2017 à 14h30.
Trollus vulgaris
Salut,
Alors je suis un peu embêté... ce que tu décris correspond bien aux coordonnées données par Wiki. Ca revient donc à s'intéresser aux mêmes accélérés en ayant décalé l'origine du repère de Lorentz à la "base" d'une hyperbole (le Bleu du dernier schéma, par exemple...). Ce qui revient donc, dans les coordonées d'origine (x,t) à retrancher 1/a et appliquer les formules, ce qui donne
L'ennui c'est que c'est exactement les coordonnées données pour Rindler simplement décalées latéralement de -1/a. La question est donc, puisque c'est exactement la même chose, Kottler-Moller est-il vraiment utile ? A mon sens non, autant prendre directement Rindler et imaginer que pour Bleu (a=0.05c/s) la cordonnée n'est pas le X de Rindler 20sl (1/0.05) mais 0... arrête moi si je me trompe mais ça ne vaut pas le coup de perdre du temps il me semble.
On peut toutefois se demander, étant donné les dates annoncées par Wiki, si la légitimité ne revient pas à KM et que l'arnaque mathématique viendrait de monsieur Rindler
Merci
Mailou
Trollus vulgaris
On en revient donc au message 44! KM = Rindler translaté. Des fois il faut un peu de temps pour trouver son propre chemin.
m@ch3
Never feed the troll after midnight!
Salut,
Oui ça doit etre ça, surtout pour qqun qui n'entend que ce qu'il veut
Tout est dit en effet :
Portant un nom different j'ai supposé que c'etait une nouvelle representation, snif.
Merci, a+
Mailou
Trollus vulgaris
Salut,
Comment tu procèdes du coup ?
Trollus vulgaris
Bonjour,
je pense que la question posée dans mon premier message reste d'actualité :
Soit O' un observateur en translation rectiligne accélérée par rapport à un référentiel inertiel K (T;X: axe longitudinal;Y:axe latéral) dans le sens positif des X.
à T=T'=0s, O' coincide avec O de K.
Si à T=0s, O voit un point P (Xp; Yp) à une distance apparente
Solution proposée : une distance apparente est une mesure locale de distance; donc on peut utiliser le principe de Rindler dans lequel un observateur accéléré fait les mêmes mesures locales de durées et de distances qu'un observateur inertiel comobile avec lui.
https://kampungpadi.files.wordpress....relativity.pdf p47
cet observateur étant inertiel, il coincide avec O à T=0s et est en MRU par rapport à lui à V; on peut donc appliquer les TLs.
Pour calculer la perspective qu'aurait un observateur Mobile de son environnement (paysage) avec une vitesse relative V suivant l'axe des X par rapport au paysage j'ai une technique que j'ai appelé effet de perspective (qui combine l'effet Doppler et l'effet d'aberration).
avec Yp'=Yp on vérifie que
Donc dans le schéma suivant si P réprésente une borne du champ,
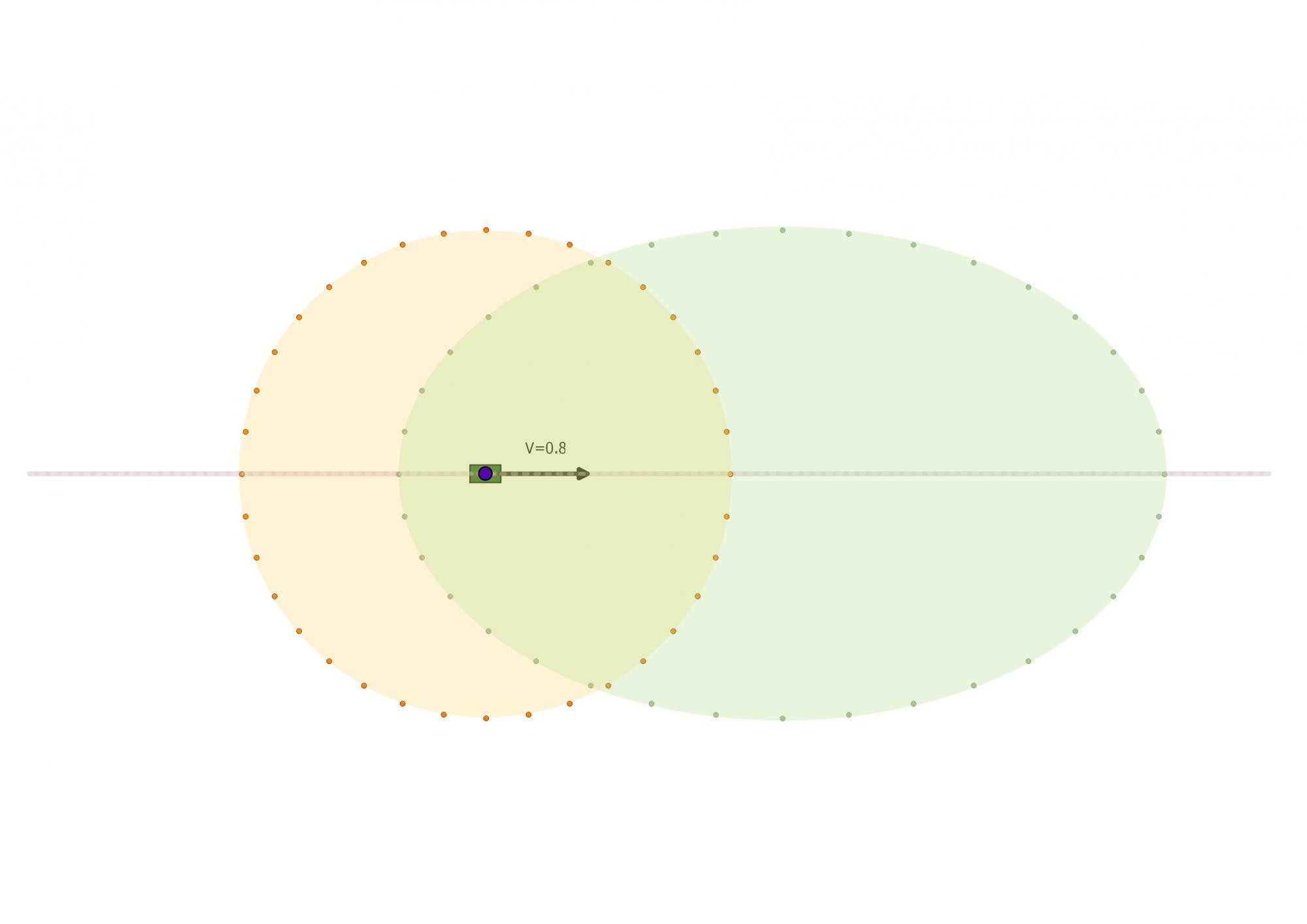
alors que O' (point violet) soit inertiel ou pas dans son wagon qui l'est, il aura la même perspective du champ à l'instant où il passera au milieu du champ.
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Je n'ai pas eu beaucoup de temps, mais c'est toujours sur ma liste de choses à voir. Une idée qui me vient néanmoins : la réponse dépend de la durée du processus de mesure. Si la mesure se réduit à un évènement unique, alors un immobile de Rindler mesurera la même chose que l'immobile de Lorentz tangent. Si la mesure ne prend pas un temps nul, elle va par contre dévier, on aura un genre de moyenne entre tous les immobiles de Lorentz qui auront été tangent pendant la mesure. En gros si la durée de la mesure est assez courte (et plus g est élevé, plus il faut qu'elle soit courte) elle donnera un résultat proche de celle fait par un immobile de Lorentz tangent.
Dans le cas particulier d'une distance radar, la mesure dure 2 fois la distance, donc pour des distances trop grandes, ça va vite déconner...
m@ch3
Never feed the troll after midnight!
C'est celà d'où la précision A T=T'=0s. Quand je dis que O' fait une mesure de distance il prend un instantanée avec un temps d'exposition de
Dire que l'immobile de Rindler voit la même chose que l'immobile de Lorentz tangent est équivalent à dire que l'observateur accéléré voit la même chose que l'observateur inertiel comobile. D'où la possibilité d'utiliser les TLs.
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Salut,
Donc on arrive bien à la conclusion que ce qui est vu n'est pas la distance radar. Je repose une dernière fois la question à tout hasard... Si on prend deux objets à égale distance d'un observateur dont l'un a une masse négligeable et l'autre une grande masse, alors puisque le second provoque un effet Shapiro qui va "ralentir" la lumière, sera-t-il vu plus loin ? Autrement dit le temps de voyage d'un photon a-t-il un impact sur ce qui est vu ?
Merci
Mailou
Trollus vulgaris
Les distances qu'on peut "voir" (avec nos yeux) sont les distances basées la luminosité ou la taille angulaire, ou basées sur l'optique, que ce soit avec la focalisation ou la vision binoculaire (parallaxe). Notons que celles basées sur l'optique nécessitent plusieurs points de captation de la lumière et qu'il faut donc une synchronisation entre eux pour pouvoir en tirer quelque chose.
On ne voit pas la distance radar, car nous ne sommes pas des radars. Dans les cas simples (notamment non relativistes) les autres mesures de distance concordent entre elles et avec la distance radar, au moins en approximation.
m@ch3
Never feed the troll after midnight!
Bonjour,
Nous sommes d'accord sur la méthode alors?
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Salut,
La distance angulaire Da correspond à la distance a l'emission (comme en cosmo) car les photons vont en ligne droite et l'angle à l'émission est invariant, et la distance de luminosité depend du mouvement de l'objet et vaudra Da(z+1) si le deplacement est lineaire et Da(z+1)^2 si le déplacement est "concentrique" par rapport à l'observateur (comme en cosmo, sauf pour les objets proches où la solution linéaire devrait etre plus adaptée). Et une sphere de matiere peut tres bien etre vue en 2D+t comme un cercle sur une sphere dont le centre ne depend que de l'observateur. (un peu HS..)
Mais je pensais plus à la vision binoculaire qui correspond (en espace plat) à Da c'est à dire la projection du cone passé sur le plan euclidien "horthogonal" au 4-vecteur instantané. Et cette projection se quantifie en mètres et si on mesure l'écart entre les deux "yeux" + 2 angles alors la trigo nous donne la distance à l'objet, en mètre et c'est bien Da. Donc il n'y a pas plusieurs notions de distance vue en RR, ce qui est vu est en quantifiable et triangulable et correspond à la distance propre pour un observateur stationnaire/MRU, sinon il y aurait des illusions (aberration)... c'est du moins comme ça que je le comprend.
Ok, seules les chauve-souris relativistes se servent de LassOn ne voit pas la distance radar, car nous ne sommes pas des radars. Dans les cas simples (notamment non relativistes) les autres mesures de distance concordent entre elles et avec la distance radar, au moins en approximation.
...
Mais.. tout ceci ne repond pas à la question : si on pose un objet massique sur le point de visée decrit précedement, est ce que ça changera quelque chose ?
Dernière modification par Mailou75 ; 30/11/2017 à 00h10.
Trollus vulgaris
Je conclue de l'absence re réponse qu'elle ne doit pas etre trivialeMais.. tout ceci ne repond pas à la question : si on pose un objet massique sur le point de visée decrit précedement, est ce que ça changera quelque chose ?
Trollus vulgaris
Bonsoir,
Pour moi, l'observateur se trouvant à la coordonnée R un objet situé à une distance radiale coordonnée
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Salut,
Peut etre, peut etre pas... demonstration stp ?
A priori comme la lumiere est "courbée" dans l'espace temps, je ne vois pas pourquoi un simple facteur donnerait la reponse. Mais n'ayant pas cette reponse je reste ouvert a toute proposition
Trollus vulgaris
Bonsoir,
Je pars de Schwarzschild pour une radiale
vilain; j'avais oublié le sqrt,.
Dernière modification par Zefram Cochrane ; 05/12/2017 à 01h54.
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Salut,Bonsoir,
Je pars de Schwarzschild pour une radiale
vilain; j'avais oublié le sqrt,
Pourquoi pas, je n'ai pas moi meme la reponse... mais tu devrais me connaitre depuis le temps, tu sais bien qu'un simple caclul ne peut me convaincre. Il faudrait le petit dessin qui prouve tout ça...
(Je vais essayer de m'y coller prochainement)
Trollus vulgaris
C'est la même méthode utilisée pour voir comment un observateur voit la vitesse de battement d'une autre horloge stationnaire sur la radiale d'un champ de gravitation par rapport à la sienne.Je pars de Schwarzschild pour une radiale
tu prends
ti poses dr'=dr=0s.l car les horloges sont stationnaires.
Ce qui fait que
ce qui donne :
Il s'agit bien là d'un écoulement apparent "du temps" de l'horloge stationnaire.
@+ Zefram
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Salut,
Pour l'ecoulement du temps relatif dans le modele de Schwarzschild on est d'accord. Mais question portait sur les distances vues. Peut etre est ce la meme chose mais j'ai bcp de mal a me le representer... ?
Trollus vulgaris
Salut, la méthode utilisée pour calculer la distance apparente étant identique à celle de l'écoulement apparent du temps relatif dans le modèle de Schwarzschild, je pense qu'elle est juste.
Si tu reprend ton schéma sur la longueur propre d'une corde tendue entre deux points, on peut peut être visualiser la longueur apparente comme étant la projection verticale de la corde sur la tangente à la courbe,matérialisant la corde, de l'observateur.
je peux croire que je sais, mais si je sais que je ne sais pas, je ne peux pas croire
Let's try... par contre ceci etant clairement HS par rapport au titre et apres avoir verifié que ça n'interesse personne sur ce forum je te propose de creer un nouveau fil dans le forum approprié
Trollus vulgaris
