Bonjour,
J'ai un (long) exercice d'électrocinétique à faire. J'ai mis après l'énoncé de l'exercice ci-dessous ce que j'ai déjà fait, merci de me dire si c'est juste, et ce qui me pose problème. Merci d'avance pour votre aide.
Voici l'exercice (les figures sont ci-dessous) :
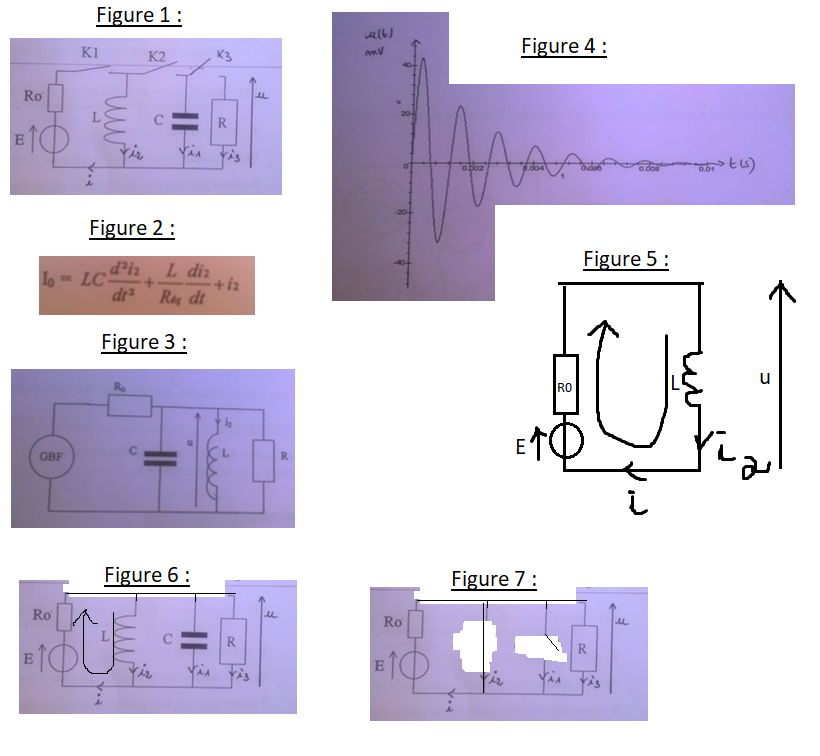
On étudie dans cette partie un circuit RLC avec le montage de la figure 1.
Au départ, les interrupteurs sont ouverts, le condensateur C est chargé avec une charge Q0 et tous les courants sont nuls. On ferme l'interrupteur K1 à t=0.
1.1 Déterminer littéralement le courant circulant dans la bobine en régime permanent et le temps qu'il faut pour atteindre ce régime à 10 % près.
On considère ce régime permanent établi et on ferme les interrupteurs K2 et K3 à un instant t que l'on considère comme nouvelle origine des temps.
1.2 Déterminer u, i1, i2 et i3 juste après la fermeture de l'interrupteur.
1.3 Déterminer u, i1, i2 et i3 au bout d'un temps très grand.
1.4 On admet qu'une source idéale de tension E en série avec une résistance R0 est équivalente à une source idéale de courant I0 en parallèle de la résistance R0 avec I0=E/R0.
Faire le nouveau schéma du montage.
1.5 Montrer que l'équation différentielle vérifiée par i2(t) s'écrit comme la figure 2 (pour plus de lisibilité), avec Req à déterminer.
1.6 Déterminer et exprimer la pulsation propre 0 du circuit ainsi que son facteur de qualité Q en fonction de R, R0, L et C. Comparer au facteur de qualité d'un circuit RLC série. Comment expliquer que l'effet de la résistance sur le facteur de qualité semble inversé ?
1.7 On veut prendre en compte la résistance interne R' de la bobine : comment sont modifiés les résultats précédents ? Dans la suite de cette partie, on négligera cette résistance R'.
1.8 Justifier qu'il existe une valeur critique de la résistance R, notée Rc que l'on exprimera en fonction de R0, L et C, qui permet de distinguer plusieurs types de régimes pour i2(t).
1.9 Dans le cas R>Rc, donner les expressions de i2(t) et u(t) en fonction de I0, 0, Q0, C et Q. Tracer l'allure de ces fonctions en précisant les temps caractéristiques. Puis tracer l'allure de u(i2). Que peut-on dire dans le cas R>>Rc ?
1.10 Dans le cas R=Rc, donner les expressions de i2(t) et u(t). On ne cherchera pas l'expression des constantes d'intégration.
1.11 Dans le cas R<Rc, donner les expressions de i2(t) et u(t). On ne cherchera pas l'expression des constantes d'intégration.
2. Caractérisation expérimentale
Un élève souhaite vérifier expérimentalement le comportement d'un circuit RLC parallèle. Il dispose pour cela d'un générateur de tension basse fréquence (GBF) de résistance interne r=50 capable de délivrer des signaux créneaux basculant entre les valeurs 0 et E avec E=6 V, de période T ajustable, et d'un oscilloscope comportant deux entrées analogiques.
Il propose le montage de la figure 3 pour le circuit.
Les valeurs de l'inductance de la bobine et de la capacité du condensateur sont respectivement L=10mH et C=4,0 F.
R correspond à une association de boîtes de résistances AOIP variables permettant d'obtenir une résistance R variable entre 0 et 10 k. La valeur de la résistance R0 est R0=500 .
2.1 Comment doit-on choisir la période T du GBF pour visualiser le régime transitoire du circuit RLC ? On donnera un ordre de grandeur de T dans le cas où R=500 .
2.2 On souhaite observer sur l'oscilloscope u(t) et i2(t). On rajoute pour cela une résistance R' de valeur faible, en série avec la bobine. Faire un schéma du montage électrique correspondant. Préciser si l'oscilloscope doit être en mode AC ou DC. Peut-on observer simultanément u(t) et i2(t) ? Préciser.
2.3 On suppose que les réglages effectués sont corrects. On obtient sur l'oscilloscope pour R=500 la courbe u(t) représentée sur la figure 4.
Commenter l'allure de la courbe observée. Les conditions initiales sont-elles les mêmes que dans l'étude théorique de la partie 1 ? Cela change-t-il les expressions de 0 et Q ?
Le type de régime obtenu dépend-il des conditions initiales ?
Déduire du signal observé le décrément logarithmique et la pseudo-période.
En déduire dans l'approximation de faible amortissement la pulsation propre et le facteur de qualité du circuit.
Ces valeurs sont-elles en accord avec ce que l'élève attendait, compte-tenu des valeurs des dipôles qu'il a utilisés ?
2.4 Quel est l'intérêt de la résistance R0, les valeurs de L et C étant toujours fixées ?
Ce que j'ai déjà fait :
1.1 J'ai dit que l'on avait un circuit équivalent à la figure 5.
Avec cela, on a :
i2=i
Avec une loi des mailles (maille orientée sur la figure), on a :
E-R0i-u=0
E-R0i-L*di/dt=0
Résolvons cette équation différentielle :
L*di/dt+R0i=E.
Ce qui équivaut à : L/R0 * di/dt + i = E/R0.
Solution de l'équation homogène : L/R0 * di/dt + i = 0
i(t)=A*exp((-t*R0)/L).
Solution particulière : E/R0.
La solution est donc : i(t)=A*exp((-t*R0)/L) + E/R0.
Avec la continuité de l'intensité du courant traversant la bobine, on a :
i(t=0+)=i(t=0-)=0=A+E/R0.
Donc : A=-E/R0.
Donc : i(t)=E/R0(1-exp((-t*R0)/L).
De plus, le régime permanent correspond à t.
En régime permanent, on a : i(t)=E/R0.
On cherche désormais le temps pour atteindre i(t)=0,9*E/R0.
Résolvons donc l'équation :
E/R0(1-exp((-t*R0)/L)=0,9*E/R0
0,1=exp((-t*R0)/L).
Donc t=(-ln(0,1)*L)/R0.
Les réponses à cette question sont-elles correctes ?
1.2 Le circuit est équivalent à la figure 6.
Avec la continuité de l'intensité du courant qui traverse la bobine, on a :
i2(t=0-)=i2(t=0+)=E0/R
On a aussi : u(t=0+)=Q0/C (comment justifier correctement cette égalité ?)
On sait aussi que u=R*i3, donc, à t=0+ Q0/C=R*i3.
Donc : i3(t=0+)=Q0/CR.
Enfin, en appliquant une loi des mailles dans la maille orientée sur la figure 6, on obtient :
E-R0i-u=0.
Donc : E-u=R0i.
Donc : E-Q0/C=R0i.
Donc : i=(E-Q0/C)/R0.
Les réponses à cette question sont-elles exactes ?
1.3 OK !
1.4 OK !
1.5 et questions suivantes : Je ne vois pas du tout comment m'y prendre, pourriez-vous me dire comment faire s'il vous plaît ? Merci d'avance.
Je vous remercie beaucoup pour votre aide et j'espère que vous m'aiderez, vu le temps que j'ai mis à poster ce message et à faire les dessins en pièce jointe...
Bon après-midi et merci.
-----




