Paradoxe en relativité (mouvement vertical)

[juliendusud]

Bonsoir,

Voici un petit paradoxe amusant en théorie de la relativité.

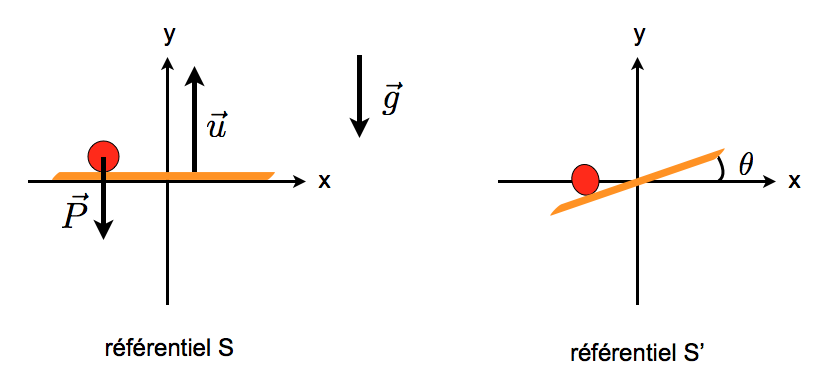
Dans un référentiel S, une plateforme se déplace verticalement à une vitesse u = u e_y.
Considérons le référentiel S' en translation uniforme à la vitesse v = v e_x par rapport à S.
Dans le référentiel S' on démontre que la plateforme est inclinée d'un angle θ par rapport à l'horizontale, avec .

Considérons un champ gravitationnel g =−g ey uniforme dirigé vers le bas.
Dans le référentiel S, la plateforme est horizontale, une bille posée sur la plateforme ne roule pas. Dans le référentiel S' en revanche, la plateforme est inclinée, on pourrait penser que la bille devrait donc se mettre à rouler. La bille ne peut pas à la fois rester immobile dans S et rouler dans S', d'où le paradoxe.

On peut penser au premier examen que les lignes de champ gravitationnel sont, elles aussi, inclinées. Mais cette inclinaison ne pourrait dépendre que de v et en aucun cas de u, or l'inclinaison de la plateforme dépend bien de u.

Comment s'en sort on?


-----

[invite06459106]

Je t'envoie une réponse en mp, histoire de laisser le plaisir à d'autres.

[mach3]

Il y a un truc fallacieux, on raisonne d'abord comme si S et S' étaient galiléens, et ensuite on dit qu'il y a un champ de gravitation, donc ils ne sont pas galiléens...
Pas de temps pour faire plus formel pour l'instant.

m@ch3

[Deedee81]

Salut,

Ca me rappelle l'histoire du paradoxe du sous-marin

Mais ici, ce n'est pas juste un problème analogue à l'aberration stellaire (comme le fait de voir les gouttes d'eau tomber en oblique quand on est en mouvement alors que la gravité est verticale (*) et aucune force appliquée horizontalement) ?
Je pose juste la question, j'ai pas creusé plus que ça.

(*) EDIT enfin, pas vraiment, justement, l'accélération de la pesanteur est oblique dans ce référentiel

[A voir en vidéo sur Futura]

[juliendusud]

Salut,

Ca me rappelle l'histoire du paradoxe du sous-marin

Mais ici, ce n'est pas juste un problème analogue à l'aberration stellaire (comme le fait de voir les gouttes d'eau tomber en oblique quand on est en mouvement alors que la gravité est verticale (*) et aucune force appliquée horizontalement) ?
Je pose juste la question, j'ai pas creusé plus que ça.

(*) EDIT enfin, pas vraiment, justement, l'accélération de la pesanteur est oblique dans ce référentiel

L'accélération de la pesanteur est bien verticale dans les deux référentiels. Pour ceux qui en doutent, il suffit de remplacer le champ de gravitation par un champ électrique, ça ne change rien aux données du problème.

[Deedee81]

L'accélération de la pesanteur est bien verticale dans les deux référentiels. Pour ceux qui en doutent, il suffit de remplacer le champ de gravitation par un champ électrique, ça ne change rien aux données du problème.

Heu, non, vérifie.

Une trajectoire de chute (dans S') est oblique (en fait une parabole) au lieu d'être verticale (c'est l'aberration). Donc dans S' g n'est pas vertical (tu peux faire une transformation de Galilée ou mieux de Lorentz du vecteur accélération si tu veux vérifier, c'est facile avec Galilée, un peu chié avec Lorentz, les formules sont lourde, de mémoire).
Et donc c'est bien normal que la bille soit immobile du point de vue de S'.

[mach3]

L'accélération de la pesanteur est bien verticale dans les deux référentiels. Pour ceux qui en doutent, il suffit de remplacer le champ de gravitation par un champ électrique, ça ne change rien aux données du problème.

Si on considère un champ électrique, alors au changement de référentiel il y a du champ magnétique qui va apparaitre... On ne peut pas faire pareil avec un champ de gravitation, à moins de prendre l'approximation gravitomagnétique. La comparaison est fallacieuse.

m@ch3

[Deedee81]

didier m'a expliqué par MP, lui est parti du transformation des forces. Ce qui au final explique aussi la situation (et ça doit forcément être cohérent avec la cinématique).

Bien vu pour le champ électrique, tu as raison, c'est totalement différent du cas des forces ou accélérations.

[juliendusud]

Heu, non, vérifie.

Une trajectoire de chute (dans S') est oblique (en fait une parabole) au lieu d'être verticale (c'est l'aberration). Donc dans S' g n'est pas vertical (tu peux faire une transformation de Galilée ou mieux de Lorentz du vecteur accélération si tu veux vérifier, c'est facile avec Galilée, un peu chié avec Lorentz, les formules sont lourde, de mémoire).
Et donc c'est bien normal que la bille soit immobile du point de vue de S'.

Non, g est bien vertical.
Tu peux le vérifier en passant par les transformations relativistes du champ électromgnétique.
Dans S, on a E = E e_y et B = 0
Dans S' : E = γ(E + v x B) = γ E donc E' (de même que g) n'a qu'une composante selon y.

Pour le champ magnétique dans S', on a :
B = γ v x E/c^2 qui n'a qu'une composante dirigée selon z.

Mais bon là je donne presque la solution.

On peut également résoudre le paradoxe en considérant seulement la transformation relativiste du poids de la boule.

[juliendusud]

Si on considère un champ électrique, alors au changement de référentiel il y a du champ magnétique qui va apparaitre... On ne peut pas faire pareil avec un champ de gravitation, à moins de prendre l'approximation gravitomagnétique. La comparaison est fallacieuse.

m@ch3

Effectivement, dans S' il y aura un champ gravitomagnétique. Mais la résolution du paradoxe ne passe pas par les champs, on peut s'en tirer uniquement en raisonnant sur le poids de la boule.

[Deedee81]

Non, g est bien vertical.
Tu peux le vérifier en passant par les transformations relativistes du champ électromgnétique.

M'enfin, tu as lu les remarques précédentes ? Le cas de g et du champ EM c'est très différent.
Et fait un peu une transformation de Galilée (juste pour faire simple) sur g, tu verras bien qu'il n'est pas vertical. C'est quand même bateau comme vérification. Même pour la vitesse c'est déjà le cas. Même pas besoin de relativité !!!! Je vais quand même pas faire une addition vectorielle pour le montrer. C'est évident.

J'ai l'impression que tu compliques à l'extrême (c'est l'impression que j'ai) alors que c'est un paradoxe franchement trivial (en faisant intervenir la gravité, le paradoxe du sous-marin c'est quand même plus costaud avec des trucs particulièrement intéressant dans le cas des TN.... quoi qu'on ne doit pas souvent aller en voyage en sous-marin vers les TN )

[juliendusud]

M'enfin, tu as lu les remarques précédentes ? Le cas de g et du champ EM c'est très différent.

Et fait un peu une transformation de Galilée (juste pour faire simple) sur g, tu verras bien qu'il n'est pas vertical. C'est quand même bateau comme vérification. Même pour la vitesse c'est déjà le cas. Même pas besoin de relativité !!!! Je vais quand même pas faire une addition vectorielle pour le montrer. C'est évident.

J'ai l'impression que tu compliques à l'extrême (c'est l'impression que j'ai) alors que c'est un paradoxe franchement trivial (en faisant intervenir la gravité, le paradoxe du sous-marin c'est quand même plus costaud avec des trucs particulièrement intéressant dans le cas des TN.... quoi qu'on ne doit pas souvent aller en voyage en sous-marin vers les TN )

En mécanique Newtonienne l'accélération, de même que la force et la masse sont des invariants.
Dès lors quand on sait g = a, comment peux tu affirmer que g pourrait varier d'un référentiel à l'autre en utilisant les transformations de Galilée, c'est bien sûr complètement faux. Le parallèle avec l'aberration de la lumière n'est pas pertinent, la lumière est un flux qui se propage à une certaine vitesse, le champ n'est rien de tel.

[Deedee81]

Je viens de me rendre compte de mon erreur. Rouge de honte. Voilà que je ne sais plus dériver des vecteurs. Pffffff

Bon, l'explication de Didier (qu'il m'a envoyé par MP) est satisfaisante amha. Qu'est-ce que tu en penses.

[invite06459106]

J'ai eu confirmation de Julien en mp, avec la démo (du coup je ne boude plus).

[juliendusud]

Je viens de me rendre compte de mon erreur. Rouge de honte. Voilà que je ne sais plus dériver des vecteurs. Pffffff

Bon, l'explication de Didier (qu'il m'a envoyé par MP) est satisfaisante amha. Qu'est-ce que tu en penses.

C'était effectivement la bonne approche.
Je ne donne pas la solution pour le moment pour laisser chercher ceux qui n'ont pas encore trouvé.

[jacknicklaus]

 Cliquez pour afficher

Il faut considérer la transformation de Lorentz appliquée à la 4-Force correspondant au poids de la bille. Les 3 composantes spatiales de la 4-Force (le nouveau "poids" de la bille) sont inclinées du bon angle dans le référentiel S'.

[Amanuensis]

Il me semble qu'on en a rien à fiche de la perpendicularité ou non. La boule est immobile par rapport à son point de contact parce qu'est nulle la somme des forces P + R dans le référentiel S. Les transformations étant linéaires, quelle que soit la valeur P' obtenue par transformation pour passer dans S', P'+R' sera nulle, et donc la bille tout autant immobile par rapport à son point de contact.

(Autrement dit, que dans S' la force de réaction R' soit perpendiculaire à la plateforme n'a rien d'évident (pas plus pas moins que pour P'), or c'est ce "raisonnement" qui amène à "penser que la bille devrait se mettre à rouler"...)