Lors du choc, au moment où la vitesse est nulle, toute l'énergie cinétique en oeuvre est alors convertie en énergie potentielle dans les matières subissant le choc élastique. C'est cette énergie potentielle qui est alors reconvertie en énergie cinétique après le choc.Envoyé par Deedee81
Excellente remarque. C'est d'ailleurs aussi pour ça que je parlais de risque de tautologie selon la manière dont on le définit.
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Apparemment l'exemple de l'atome radioactif qui se désintègre n'est pas un bon exemple ici.
Si je résume ce qui a été dit, cette désintégration pourrait ne pas admettre une description utilisant un pur formalisme quantique quant à sa cause (enfin c'est ce que j'ai compris). Divers points de vue ont été avancés selon qu'une éventuelle cause extérieure à la désintégration devrait se manifester ou non par un apport (ou une perte) d'énergie au système. La réponse à cette dernière question semble être que non, pas forcément.
Un autre argument est que l'observation de ce phénomène, dans sa description, ne fait pas appel à une "observable" décrite en mécanique quantique qui admette une "observable" complémentaire et non-commutante, ce qui, si c'était le cas, justifierait (selon Amanuensis) que seule la MécaQ est apte à décrire ce phénomène.
et là :
Je n'ai pas bien compris la relation entrer ce dernier argument et notre "expérience", j'ai intuité que cela est peut-être lié à l'absence d'opérateur "temps" en mécaQ ( et qu'ainsi on ne peut pas formaliser mathématiquement d'observable complémentaire à l'opérateur énergie, i.e. l'hamiltonien.) En supposant que ce soit la "mesure d'énergie" qui soit impliquée ici (à savoir celle du photon ou de la particule émise par désintégration radioactive), cela semble cohérent avec ce que vous énoncez, Amanuensis. Suis-je dans le vrai?
Bon Bref, et bien si cette "expérience" n'est pas signifiante dans notre problématique, peut-être peut-on en aborder une autre : bien sûr l'expérience des fentes d'Young. , ou en tout cas une de ses variantes qui consiste à envoyer des électrons un par un sur un dispositif appelé biprisme, l'expce de Merli–Missiroli–Pozzi "Two-Slit Electron-Interference Experiment." réalisée en 1974, ou celle de l'équipe de Tonomura (1979).
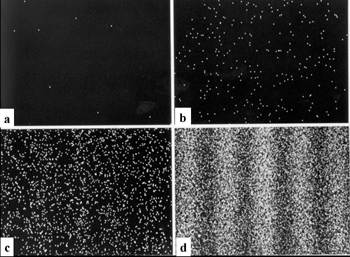source image : le lien cité plus bas. (expérience par équipe Tonomura)
Au début (fig.a et b) les quelques premiers électrons captés sont bien "localisés" et à la fin (fig. d) on voit apparaître la figure d'interférence.
Chaque électron qui touche l'écran produit un évènement macroscopique (une "tache" sur l'écran), dont la localisation est indéterministe (au sens cette tache peut apparaître à un endroit ou à un autre), et son explication a pour fondement un formalisme quantique (fonction d'onde de l'électron). On a ici une observable renvoyant à l'opérateur "Position" qui admet bien un complémentaire non-commutant l'opérateur "Quantité de Mvt".
Cela pourrait-il convenir ou pas? (comme exemple d'indéterminisme macroscopique d'origine quantique comme défini ci-avant dans message #18)
J'avoue que la réalisation de cette expérience est pour moi un mystère.
Mon questionnement étant : Comment diable arrive-ton à mettre en place un dispositif qui envoie les électrons un par un (et pas un flux macroscopique d'électrons) ? Comment chaque électron (qui est une particule microscopique) peut-il provoquer une tache sur l'écran qui soit apparemment "visible à l'œil nu" et donc "macroscopique" ?
Une description ici pour une expérience réalisée par l'équipe de Tonomura : (lien repris sur Wikipedia)
Hitachi website that provides background on Tonomura video and link to the video
http://www.hitachi.com/rd/portal/hig...lit/index.html
Mais il s'agit d'une description très sommaire.
Ici description un peu plus précise de l'expérience de Merli–Missiroli–Pozzi :
https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4617474
N'ai pas trouvé le papier initial, qui doit mieux décrire le dispositif (ai fait la demande sur ResearchGate) :
Merli, P G; Missiroli, G F; Pozzi, G (1976). "On the statistical aspect of electron interference phenomena". American Journal of Physics. 44: 306–307.
Dernière modification par ulyss ; 19/05/2018 à 15h04.
L'expérience a été réalisé en 2003 et le papier est en accès libre : http://iopscience.iop.org/article/10.../3/033018/meta
Il répondra à toutes vos questions. Pour les électrons un par un, tout bêtement une source de faible intensité... Pour la figure "macroscopique", il y a un des champs EM qui jouent le rôle de lentille.
Par ailleurs, oui, cet exemple est correct. La non-commutativité est entre l'observable position (où est ou va être l'impact) et la vitesse (en fait la quantité de mouvement) en tant que vecteur. Car observer la vitesse vectorielle (sa direction) à l'impact ou avant l'impact revient à observer par quelle fente la particule est passée.
Et de nombreuses variantes de l'expérience ont porté justement sur si et comment on pouvait mesurer la quantité de mouvement, avec comme conclusions que cela détruisait les figures d'interférence sur l'écran.
À cause de cet effet seul le modèle quantique donne des prévisions correctes du phénomène observé.
Dernière modification par Amanuensis ; 19/05/2018 à 18h22.
Pour toute question, il y a une réponse simple, évidente, et fausse.
Par ailleurs encore:
C'est un effet d'amplification, comme ce qu'il se passe dans un photomultiplicateur ou dans la rétine. L'impact crée une modification microscopique (par exemple d'un seul atome) qui va être amplifiée en des modifications d'un nombre bien plus grand d'atomes, un peu comme un seul domino qui tombe peut déclencher la chute d'une grande quantité d'autres dominos.Comment chaque électron (qui est une particule microscopique) peut-il provoquer une tache sur l'écran qui soit apparemment "visible à l'œil nu" et donc "macroscopique" ?
Et cet effet d'amplification est essentiel dans le passage micro/macro, c'est ce qui est modélisé par une «décohérence»: quand un état non propre pour une observable est forcé d'interagir avec quelque chose qui va amplifier les états propres (pour cette observable), le système «décohère».
C'est aussi pour cela qu'on ne pas observer inter-subjectivement un état non propre (avec observer au sens d'une observable pour lequel l'état n'est pas propre) : il faut que la mesure soit au moins multipliée par deux.
(Ces explications viennent de je ne retrouve plus quel chercheur spécialiste connu dans le domaine... Viennent de au sens de ce que j'ai lu et cru comprendre.)
Pour toute question, il y a une réponse simple, évidente, et fausse.
Intéressant cette double mesure! Un lien avec le théorème d’échantillonnage de Claude Shannon?
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
Il y a un lien mathématique fort entre la théorie du signal et la PhyQ (le mot important étant «mathématique»).
Pour toute question, il y a une réponse simple, évidente, et fausse.
Et en un peu plus précis que mathématique?
Moi ignare et moi pas comprendre langage avec «hasard», «réalité» et «existe».
Dans l'hypothèse où la désintégration du noyau serait provoquée par une force extérieure, cette force en s'exerçant ne doit-elle pas nécessairement apporter ou retirer de l'énergie au noyau ?
D'une manière générale, lorsqu'une force s'exerce sur un objet, n'y a-t-il pas nécessairement un transfert d'énergie, comme cela se vérifie avec la force d'attraction qui, au niveau d'une planète et de son satellite, induit des effets de marées, un ralentissement des vitesses de rotation, un accroissement des distances et au final un accroissement de l'énergie potentielle ?
Une force quelle qu'elle soit peut-elle s'exercer sans apporter ou retirer de l'énergie à l'objet sur lequel elle s'exerce ?
La grossièreté et l'invective sont les armes préférées d'une pensée impuissante.
Faut-il répéter toutes les réponses déjà données?
Et si oui, pourquoi? Parce qu'elles n'ont pas été données par un modérateur?
Dernière modification par Amanuensis ; 23/05/2018 à 20h01.
Pour toute question, il y a une réponse simple, évidente, et fausse.
Salut,
Mais on a déjà répondu à toutes ces questions. Je ne comprend pas pourquoi tu les reposes encore. Peut-être n'as-tu pas compris les réponses ? Mais dans ce cas il faut préciser ce que tu n'as pas compris, sinon tu ne vas pas avoir de meilleures explications.
Prenons un exemple avec ta dernière question :
La réponse est oui. Deux exemples :
- Une force centrale (par exemple la gravité ou une force de traction mécanique dans un manège) agissant sur un corps en rotation circulaire. Le travail est nul.
- Les forces magnétiques sur une charge électrique : travail toujours nul (cela résulte directement de la force de Newton-Lorentz, la force magnétique est perpendiculaire au mouvement, quel qu'il soit).
Est-ce que quelque chose te chiffonne dans cette réponse ? Si oui, pourquoi ?
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Je suis sincèrement désolé, j'ai en effet essayé de reformuler plus précisément la question car j'ai eu l'impression dérangeante que certaines réponses apportées (par toi et par Amanuensis) induisaient une violation du principe de conservation de l'énergie...
Dans le cas du manège, il arrive pourtant malheureusement que la nacelle se décroche sous l'effet de la force centrifuge. N'est-ce pas la preuve que le travail n'est pas nul au niveau du corps en rotation ?
Oui, en effet, la force de Lorentz provoque un déplacement de la charge en mouvement sans aucun échange d'énergie (il faut que je revoie la relation entre force et énergie) !
Autrement dit, une force peut exercer une action sans échange d'énergie.
Toutefois, cela est-il suffisant pour supposer que la désintégration du noyau ne serait pas un phénomène spontané mais pourrait être provoquée par une force cachée ?
La grossièreté et l'invective sont les armes préférées d'une pensée impuissante.
Dans ce cas il ne doit pas être nul, mais pas très longtemps, le temps de la déformation plastique et rupture sous l'effet de la contrainte interne.
Avant déformation et rupture il n'y a pas de travail (bien qu'une telle déformation doit être assez progressive, avec déplacement des défauts cristallins dans le métal, voire intervention des vibrations et autres chocs) et une fois libérée il n'y a plus de travail (sauf bien entendu la force de gravité, malheureusement pour le malheureux dans la nacelle qui va forcément durement apprendre les lois de Newton lorsque la nacelle va touche le sol, et là le travail des forces de frottement sur le sol).
Evidemment, le manège il faut bien le mettre en route, là aussi il y a transfert d'énergie.
Non, ce n'est pas suffisant, tu as raison.
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Je pensais a priori que c'était suffisant... Pourquoi n'est-ce pas suffisant pour retenir l'hypothèse d'une force cachée à l'origine de la désintégration ?
Dernière modification par andretou ; 24/05/2018 à 15h35.
La grossièreté et l'invective sont les armes préférées d'une pensée impuissante.
Parce que les forces intervenant dans l'interaction nucléaire sont extrêmement complexe et ça ne se résume pas à "forces qui travaillent ou pas".
Sans compter que c'est quantique.
On peut modéliser le processus par une barrière de potentiel et l'effet tunnel, mais ça reste un modèle heuristique, ça ne prouve pas le mécanisme.
Et les modèles plus sophistiqués (comme les modèles en couches intégrant l'isospin et autres joyeusetés) c'est aussi des modèles approchés.
On peut très certainement faire confiance à l'équation de Schrödinger, suffisamment testée, mais impossible de résoudre le bousin complet à l'aide de cette équation. Trop compliqué.
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Dites pourquoi au lieu de vous contenter de remarques vagues. Ayez une démarche scientifique. Vous soulevez un lièvre, c'est à vous d'apporter des arguments contradictoires, pas à Deedee81 de vous prouver que la conservation de l'énergie est saine et sauve.
Dernière modification par albanxiii ; 24/05/2018 à 20h38.
Not only is it not right, it's not even wrong!
Oui le régime chaotique est indéterministe, et c'est lié à l'impossibilité de déterminer avec une précision arbitraire les conditions initiales.
C'est lié aux instruments de mesure, ou à la complexité du système étudié d'un point de vue macroscopique.
Mais même à imaginer des instruments de mesure parfait,
L'imprécision des conditions initiales trouverait une justification théorique dans la physique quantique,
Avec le principe d'indétermination d'Heisenberg.
Cordialement,
Oui c'est suffisant.
Sauf que c'est totalement inverser la logique argumentaire!
C'est dans l'autre sens, l'argument de l'absence d'échange d'énergie au bilan (c'est à dire calculée entre bien avant l'interaction et bien après l'interaction) ne peut pas être un argument suffisant pour réfuter l'intervention d'une «force» avec l'extérieur.
Les arguments pour défendre l'idée que la désintégration spontanée d'un noyau soit totalement «acausale», ne mettant en jeu aucune «force» avec son environnement, doivent être cherchés ailleurs.
(Je ne dis pas qu'il n'y en a pas, je dis juste que l'argument portant sur l'absence d'échange d'énergie au bilan ne tient pas la route. Faut passer à d'autres arguments. Lesquels?)
Dernière modification par Amanuensis ; 25/05/2018 à 07h40.
Pour toute question, il y a une réponse simple, évidente, et fausse.
Bonjour,
Cette impossibilité de reproduire des conditions initiales maîtrisées n'est pas ce qui est discuté dans ce fil. Par ailleurs, l'extrême sensibilité à des conditions initiales (définition d'un système chaotique) n'exclut pas le déterminisme.
Salut,
Et pour cause, on l'appelle le chaos déterministe !
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Si on considère 1 désintégration (d'un noyau, d'un neutron...) prise individuellement, je pense que rien ne permet en effet de rejeter l'hypothèse d'une force cachée à l'origine de la désintégration.Autrement dit, une force peut exercer une action sans échange d'énergie.
Toutefois, cela est-il suffisant pour supposer que la désintégration du noyau ne serait pas un phénomène spontané mais pourrait être provoquée par une force cachée ?
En revanche, si on considère un ensemble suffisamment grand de noyaux radioactifs (ou de neutrons), alors on constate que les désintégrations se produisent selon une loi de décroissance exponentielle. Or, par le jeu des probabilités appliquées au grands nombres, seules des désintégrations parfaitement aléatoires - donc "acausales" - ont pour signature une décroissance exponentielle.
De ce fait, je pense qu'on peut affirmer que la désintégration du noyau est un phénomène parfaitement aléatoire, qui ne peut donc avoir pour origine aucune force cachée.
Ce raisonnement te paraît-il correct ?
Dernière modification par andretou ; 25/05/2018 à 17h56.
La grossièreté et l'invective sont les armes préférées d'une pensée impuissante.
Pas pour moi, j'explique.
La loi exponentielle est juste la loi «par défaut», elle est celle obtenue quand les événements en question sont totalement indépendants. On parle de loi «sans mémoire», car si on fait l'hypothèse que la probabilité d'un événement ne dépend en rien du passé, alors on obtient cette loi.En revanche, si on considère un ensemble suffisamment grand de noyaux radioactifs (ou de neutrons), alors on constate que les désintégrations se produisent selon une loi de décroissance exponentielle. Or, par le jeu des probabilités appliquées au grands nombres, seules des désintégrations parfaitement aléatoires - donc "acausales" - ont pour signature une décroissance exponentielle.
Cette loi est donc comparable dans sa catégorie à la loi gaussienne, ou une loi uniforme (iid) ; ce sont des lois définies par très peu de paramètres, et du coup très peu informatives. (Un seul pour la loi exponentielle, la demi-vie. Pas facile de faire moins pour une loi non dégénérée. Pour toute loi d'arrivée on peut parler d'une demi-vie (ou son équivalent) pendant telle période, mais la loi exponentielle est la seule qui soit définie entièrement par ce seul paramètre (dont on tire aussi bien la moyenne du nombre d'arrivées par intervalle de temps, son écart-type, etc.), d'où l'idée de «loi par défaut».)
Il est très courant de présenter ces lois «par défaut» comme «parfaitement aléatoires», mais l'adjectif s'applique à des lois de probabilité, pas aux phénomènes qu'elles modélisent.De ce fait, je pense qu'on peut affirmer que la désintégration du noyau est un phénomène parfaitement aléatoire
Tout ce qu'on sait expérimentalement, c'est à dire du fait que les observations sont compatibles avec la loi «sans mémoire» est qu'on peut supposer que les désintégrations ne sont pas corrélées entre elles, donc ne sont ni manifestement cause l'une des autres, ni manifestement des effets d'une même cause.
Comme c'est une loi peu informative, on est bien ennuyé, car cela ne donne pas d'information sur les causes éventuelles, on a seulement l'information que s'il y en a, elles ne manifestent pas par la loi observée.
(Ce serait différent si par exemple l'observation était compatible avec une loi exponentielle «à petite échelle», avec le paramètre variant lentement avec le temps, par exemple. On aurait une donnée supplémentaire utilisable pour chercher ou tester une influence extérieure.)
Pour toute question, il y a une réponse simple, évidente, et fausse.
Supposons donc que le désintégration ne soit PAS un phénomène parfaitement aléatoire, et qu'il existe donc une force cachée et donc un paramètre caché qui régit ou influence le phénomène : dans ce cas, le paramètre caché ne devrait-il pas nécessairement influencer la loi de décroissance qui du coup ne devrait pas être rigoureusement exponentielle ?...
La grossièreté et l'invective sont les armes préférées d'une pensée impuissante.
Pas si le phénomène caché est lui-même «aléatoire», mais le dire comme cela ne fait que déplacer le problème.
De nombreux phénomènes avec une explication causale claire suivent néanmoins une loi «loi aléatoire», une de ces lois simples à peu de paramètres, qu'on appelle couramment aléatoires.
Le cas le plus courant est quand la «cause» est une combinaison d'un grand nombre de causes non corrélées entre elles et de «poids» comparables.
Autrement dit la loi des grands nombres est très souvent l'origine (pas la cause physique!) de l'observation d'une ce ces «lois simples», dont la loi exponentielle fait partie.
Et le domaine qui couvre cela n'est pas la mécanique quantique, mais la physique statistique.
---
En clair la seule observation d'une loi simple (dite «aléatoire») ne permet pas de distinguer un phénomène explicable causalement et traité dans le cadre de la physique statistique d'un phénomène qu'il faut traiter par la physique quantique.
Dernière modification par Amanuensis ; 25/05/2018 à 20h31.
Pour toute question, il y a une réponse simple, évidente, et fausse.
Merci pour vos réponses, et pour le lien vers le papier fourni par Coussin. Désolé, je n'ai pas toujours le temps de répondre très rapidement.
La raison pour laquelle j'ai ouvert cette discussion est que, bien souvent, lors de conversations sur des forums ou autre à propos du "déterminisme des phénomènes physiques" ou plus généralement du "déterminisme du monde" on entend des remarques qui renvoient à la mécanique quantique. Certains déclarent en effet que, la MécaQ étant intrinsèquement indéterministe (renvoyant au principe d'indétermination de Heisenberg), alors cela permettrait de "trancher" en quelque sorte le débat.
Je me suis alors demandé alors si cet "indéterminisme quantique" pouvait réellement s'immiscer en quelque sorte dans le monde macroscopique (ou non), d'où la question dans le strict sens qui a été défini dans notre discussion.
Bien évidemment, la question plus générale "le monde est-il déterministe?", bien qu'intéressante, est une question qui est à la limite de la philosophie et de la physique (et d'autres domaines) et il serait hasardeux (ou même peut-être fallacieux) de prétendre que la physique puisse apporter une réponse définitive. En conséquence cela sortirait du cadre de ce forum "Physique Futura-Science". Néanmoins la physique peut apporter un éclairage sur cette question.
Il convient donc de reformuler cette question (comme réalisé ici), à savoir "les phénomènes macroscopiques expliqués et prédits par les sciences physiques montrent-ils un indéterminisme, et, si oui, cet indéterminisme peut-il avoir une origine quantique" .
Mais revenons à la discussion.
Un aspect a été évoqué par Eldor, le phénomène du chaos quantique :
Ce "chaos quantique" entre-t-il de manière pertinente dans notre sujet, en ce sens qu'il pourrait se traduire par un indéterminisme macro? Ou est-ce encore un "chaos déterministe" comme mis en lumière plus tôt par Deedee81 ?
Par exemple, dans l'article :
https://www.futura-sciences.com/scie...it-bien-20764/
est évoqué le cas du satellite Hypérion de Saturne.
D'autre part il a été discuté ici de 2 cas particuliers, la désintégration d'un atome radioactif et les fentes d'Young.
J'aimerai élargir pour voir s'il y a des cas entrant dans des descriptions actuelles plus globales dans les différents domaines des sciences, par exemple :- cosmologie : les modèles actuels qui expliquent par exemple la formation des galaxies, des étoiles, des systèmes stellaires, ou le "fonctionnement" d'une étoile peuvent-ils mettre en lumière un tel "indéterminisme d'origine quantique" dans le sens où par exemple, une caractéristique stellaire macro pourrait être A ou B... ?Bien entendu on resterait dans le cadre de la discussion, à savoir mettre en lumière des indéterminations "dues" à la MécaQ.
- chimie : idem pour les phénomène chimiques...?
- biologie : idem (on peut penser aux mutations des gènes par ex.)
- neurologie.
- etc...
Dernière modification par ulyss ; 28/05/2018 à 17h31.
Thus determinism lapses completely into indeterminism as soon as the slightest inaccuracy in the data on velocity is permitted. Is there any sense - and I mean any physical sense, not metaphysical sense - in which one can speak of absolute data? [...] It is only necessary to replace statements like x = π cm by: the probability of distribution of values of x has a sharp maximum at x = π cm; and (if it is desired to be more accurate) to add: of such and such a breadth. [...] the determinism of classical physics turns out to be an illusion, created by overrating mathematico-logical concepts. It is an idol, not an ideal in scientific research, and cannot therefore be used as an objection to the essentially indeterministic statistical interpretation of quantum mechanics. https://www.nobelprize.org/nobel_prizes/physics/laureates/1954/born-lecture.pdf Ainsi, le déterminisme tombe complètement dans l'indéterminisme dès que la moindre inexactitude dans les données sur la vitesse est autorisée. Y a-t-il un sens - et je veux dire un sens physique, pas un sens métaphysique - dans lequel on peut parler de données absolues? [...] Il est seulement nécessaire de remplacer les déclarations comme x = π cm par: la probabilité de la distribution des valeurs de x a un maximum net à x = π cm; et (si l'on veut être plus précis) ajouter: de telle ou telle largeur. [...] le déterminisme de la physique classique s'avère être une illusion, créée par une surestimation des concepts mathématiques-mathématiques. C'est une idole, pas un idéal dans la recherche scientifique, qui ne peut donc être utilisée comme une objection à l'interprétation statistique essentiellement indéterministe de la mécanique quantique.
Votre réponse est intéressante, Nicophil.
Elle peut nous amener à réfléchir sur le sens de ce qu'est le déterminisme/indéterminisme, de ce qu'un déterminisme peut être considéré comme absolu ou approximatif, et dans quelle mesure cela a une signification dans la perspective de la science physique.
Néanmoins dans le message 18 je définis ce qu'est un état macroscopique (définition usuelle) : c'est la donnée (ou la mesure) d'une série de grandeurs physiques, à savoir un champs de pression, de température, de concentrations molaires volumiques etc... avec une "maille" macroscopique, à savoir avec une "granularité/précision" dV (volume ou dx, dy, dz), dt (temporelle), mais aussi un epsilon dG pour chaque grandeur physique G. La limite inférieure des dx, dy, dz, dt, dG est difficile à fixer.
Mais avec cette définition on passe "sous la fourche" de votre remarque.
Dans ce message 18 je fais aussi l'hypothèse que l'on puisse décrire microscopiquement un système macroscopique. Le système macro considéré S est supposé "décomposable" en N sous-systèmes (Si) assez petits (des atomes par exemple) pour que chaque (Si) n'admette qu'une description efficace de type quantique (exemple des atomes ou des particules).
Les exemples mis en avant pour l'instant ne montrent que des systèmes où l'on ne va décrire quantiquement qu'un tout petit sous-système (un seul atome radioactif, ou un seul électron arrivant sur l'écran), et pas "tout le système".
Je ne sais pas d'ailleurs si une description "micro/quantique" de l'ensemble d'un système macroscopique a un sens. En effet les innombrables sous-systèmes vont fatalement interagir, et on va avoir ainsi des phénomènes d'intrications quantiques, et des effondrement de fonction d'onde au sein même de sous-parties du système macro S (avant que l'on fasse la mesure macroscopique finale) dus aux interactions... dès lors peut-on espérer décrire "tout" le système S à un instant t de manière "microscopique/quantique", dans le sens cela est-il possible en pratique ou même en théorie? Je n'en sais rien.
Dernière modification par ulyss ; 28/05/2018 à 21h52.
Si on cherche des exemple, il existe il me semble un exemple général trivial que l'on a tendance peut-être à occulter : "Toute mesure quantique." Après, c'est le "peut" qui me parait important, puisqu'il existe, il me semble à nouveau, des cas où la mesure est parfaitement déterministe (sous condition) et d'autres cas où la mesure est statistique. Si, depuis un appareillage macroscopique, on prépare un objet d'étude quantique à deux états pour que sa valeur soit DEFINIE, puis on le mesure, la VALEUR de cette première mesure sera indéterminée (Ce n'est d'ailleurs pas un problème spécifiquement quantique, mais un problème lié à toute mesure, puisque pour mesurer une valeur qui ait du sens, il faut se référer à un troisième système) . Mais si on mesure à nouveau l'objet d'étude préparé dans les mêmes conditions et qu'on le mesure avec le même appareil macroscopique, sa valeur sera déterminée (le système de référence étant la première mesure...). Il n'y a donc rien d'aléatoire ici et le postulat que les mêmes causes produisent les mêmes effets reste vrai, même dans le monde microscopique. Par contre, si on prépare un objet d'étude du type "fonction d'onde", alors on ne peut pas déterminer la valeur que prendra la mesure. Ce sera une mesure statistique. Néanmoins, et c'est là peut-être le point à méditer, on peut préparer un objet de ce type pour que statistiquement la valeur mesurée soit plus souvent proche d'une certaine valeur... Après, à mon avis, c'est peut-être juste une question de point de vue sur la catégorisation : Une fonction d'onde d'une certaine "forme" est-elle le même objet qu'une fonction d'onde d'une autre forme ? Est-ce une "préparation" au même titre que le cas précédemment évoqué ?Le macroscopique peut-il être indéterministe du fait de phénomènes quantiques?
Bonjour,
Je voulais revenir sur cette discussion.
Le motif initial était de savoir si l'indétermination au niveau quantique/microscopique pouvait s'immiscer dans le macroscopique.
Nous avons mis en lumière l'expérience des fentes d'Young.
J'ai essayé d'élargir la réflexion à d'autres niveaux (cosmologique, biologique, neurologique, etc...).
Je me posais la question, qui j'espère ne vous choquera pas, de phénomènes neurologiques, en particulier de la conscience.
Aujourd'hui on pense que le siège de l'esprit est dans le cerveau. En particulier les pensées, puis les actes, les décisions humaines sont la conséquence du fonctionnement physico-chimique de cet ensemble de 100 milliards de neurones, chaque neurone étant lié aux autres par des synapses (environ dix-mille à cent milles synapses par neurone). Certains disent que le cerveau humain est l'objet physique le plus compliqué de l'univers.
Ma question est : est-il concevable que le fonctionnement macroscopique du cerveau montre un indéterminisme global d'origine quantique. Est-il possible qu'une personne puisse faire un choix A ou un choix B parce qu'une réduction de paquet d'onde mène soit à l'état macro A, soit à l'état macro B ?
En gros existe-t-il des réduction d'onde correspondant à des fonctions d'ondes quantique "macroscopique", qui en l'occurrence se traduirait par un indéterminisme des états de conscience...
J'envisage plusieurs réponses :
1) le cerveau est un objet macroscopique beaucoup trop gros. Il ne peut être dans des états quantiques superposés. Le fonctionnement est forcément déterministe, ou en tout cas il ne peut y avoir d'indéterminisme d'origine quantique.
2) En l'état de nos connaissance on ne peut rien dire, sinon émettre de pures spéculations. Cette approche que je propose, qui consiste à vouloir expliquer un domaine (la psychologie humaine, la conscience) par un autre domaine scientifique (la physique) relève, en l'état de nos connaissances, d'une sorte de réductionnisme, et, si on commence à vouloir tirer des conséquences, de la pure para-science.
3) Oui, il est tout à fait possible que le fonctionnement du cerveau, et ses conséquences (par exemple le comportement humain), puisse monter une indétermination d'origine quantique.
Merci pour vos réponses...
Dernière modification par ulyss ; 18/10/2018 à 14h18.
