Bonsoir,
J'ai consulter plusieurs sujet crée sur des forum par des internautes mais aucun n'a réussi a m'expliquer concrètement ce que signifie dériver un vecteur.Je me tourne donc vers vous. Please !
En effet, dans la physique mécanique on dérive ou intègre des vecteurs accélération, vitesse ou position pour obtenir l'un ou l'autre.
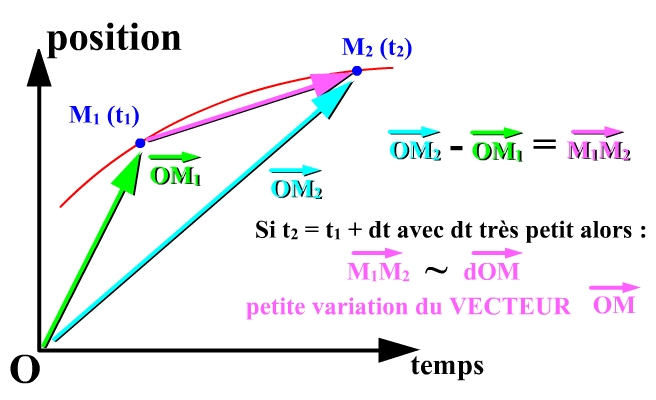
Le problème est que la notion de dériver un vecteur je n'arrive pas a la schématiser dans ma tête. Un vecteur pour moi c'est simplement une "flèche" qui indique le sens et la direction du déplacement d'un objet. Comment ce "déplacement" peut être dériver ?
On dérive des fonctions pour étudier des variations ect... mais pas des vecteurs, enfin je n'arrive pas a saisir.
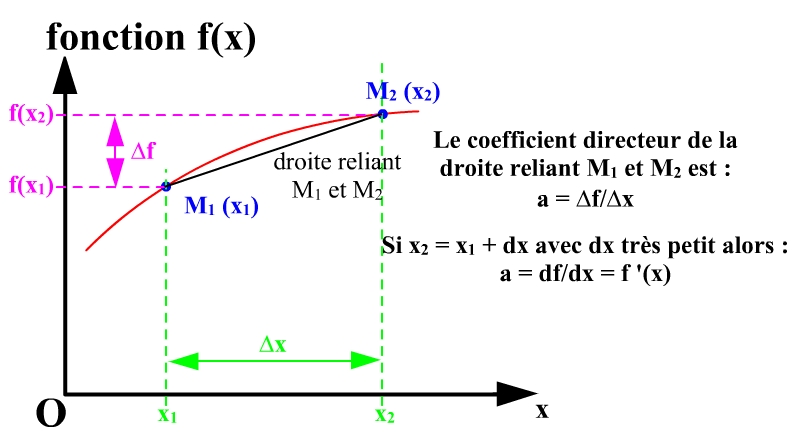
Par définition "la valeur de la dérivée en un point M de la courbe correspond au coefficient directeur de la tangente à la courbe au point M...".
De plus, la vitesse en fonction du temps v(t) c'est comme f(x), on a la vitesse v(t) en ordonnée et le temps t en abscisse. La dériver donne logiquement une fonction v(t)' = a(t). Mais en physique, la notation est dv/dt=a(t) . C'est cette fraction que me pose problème. Comment une dérivée peut donner une fraction de deux grandeurs, comment la noterez-vous cette dérivée sans cette fraction... ? v(t)'=dv/dt ? Parce que v(t)' c'est une expression d'une fonction alors que dv/dt c'est un rapprochement infinitesimale : (voir image joint)
Capture2.PNG
Mais mes principaux problème sont avec les normes des vecteurs... Quand je rédige un exercice, je ne sais jamais quand il faut mettre la flèche sur le vecteur.
Comment différencier la norme et le vecteur ? par exemple, je mesure a la règle la taille du vecteur vitesse, ensuite j'ecrit vecteur(v)=2.5, on me dit
qu'un vecteur(a) n'est pas égale a sa norme.
De plus pourquoi un vecteur est égale a la somme de ses coordonnées ? On peut pas additionner ses coordonnées comme ça, on les écrit au préalable entre parenthèse ( x ; y ; z ) (voir image joint). Ah moins que c'est la décomposition du vecteur ? on multiplie ainsi ses coordonnées par les vecteurs unitaires c'est ça ? Capture.PNG
Comme la plupart des élèves je sais appliquer et travailler avec tout ce que j'ai cité précédemment mais sans comprendre ce que c'est vraiment.
S'il vous plait ! même si vous me vulgariser la chose ou juste avec des mots simple pour que je puisse comprendre, appréhender la signification...
J'accepte volontiers toute aide et je remercie sincèrement d'avance les personnes qui auront la patience de m'expliquer cela.
-----





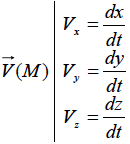

 compris, vos réponses m'ont bien illustrer la chose.
compris, vos réponses m'ont bien illustrer la chose.