Périmètre Ellipse

[Drt31]

Bonjour,
Je ne trouve aucune formule comment calculer le périmètre en fonction de ses dimensions : sur le web ou dans mon encyclopédie Larousse, on ne peut obtenir qu'une approximation.
J'ai un aide mémoire "THECNOR" de P.HEINY où on trouve que les formules de surfaces :
Pour le cercle de diamètre D, son périmètre appelée circonférence est égal au produit du diamètre par le nombre pi (Л) donc P = D * Л;
Et la surface S = Л * D² / 4 s'écrivant aussi D² * Л/4
Comparé au carré circonscrit dont le côté est égal a D, sa surface est égale à D²
D'où la surface du cercle qui est égale Л * D²/4, on peut dire que cette surface du cercle est égale à la surface du carré circonscrit multiplié par Л/4.
Dans l'aide mémoire, on trouve la surface de l'ellipse qui a pour grand diamètre la valeur "a", le petit diamètre, la valeur "b", "a" et "b" correspondent aussi aux dimensions du rectangle circonscrit.
Surface ellipse S = (Л *a * b)/4 pouvant s'écrire aussi = (a * b) * Л/4.
Ici, il n'y a pas d'approximation.
J'ai donc comparé le quart de l'image du carré avec son cercle inscrit avec le rectangle avec son ellipse inscrite.

Il apparait que l'on trouve pour le cercle en abscisse la valeur D/2, de même qu'en ordonnée, la somme de ces 2 segments est égale à la valeur du diamètre D. Similairement, pour l'ellipse, on aura a/2 et b/2 !!Л
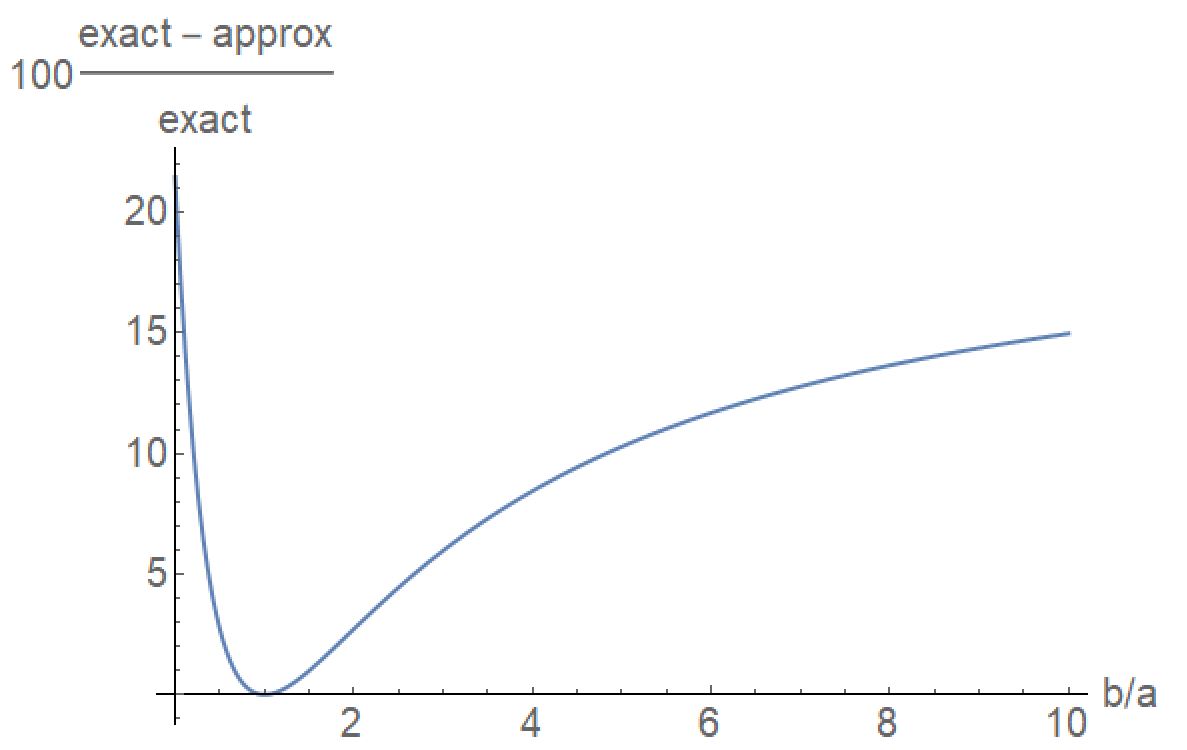
Donc, dans la même image, on peut dire que le périmètre d'une ellipse est égale (a + b)/2 * Л s'écrivant aussi P ellipse = (a + b) * Л/2
J' ai vérifié physiquement en découpant 3 ellipses de dimensions différentes, et en mesurant celles-ci, je trouve une valeur pratique meilleure que 1% par rapport au calcul.

Drt31 Transmis pour information.
-----

[coussin]

Il y a beaucoup d'approximation mais pas de formule simple exacte. La formule exacte fait intervenir une intégrale elliptique.

https://en.m.wikipedia.org/wiki/Ellipse#Circumference

[Drt31]

Bonjour,
C'est ce que je disais : que pensez-vous de la formule simple que j'ai énoncée ci-dessus : Périmètre ou circonférence ellipse = petit diamètre + grand diamètre, le tout multiplié par pi/2 c'est à dire x par 1,57 qui inférieur à 2, ce dernier étant le périmètre du rectangle circonscrit.
Comparé au cercle et son carré circonscrit, on retrouve la même formule (D + D) x pi/2 soit 2D * pi/2 qui se réduit à D* pi.

On peut démontrer facilement la surface du cercle en considérant une multitude de triangle dont le sommet est le centre du cercle, et que la somme des bases entourant le cercle est bien la longueur de la circonférence, la hauteur du triangle se confond à la valeur du rayon d'où S = pi * R² ou = pi * D²/4

Drt31

[coussin]

Oui, vous faites la moyenne entre les cercles ayant comme diamètres le petit et le grand axe. C'est l'approximation qu'on rencontre souvent.
Ça doit pas mal marcher si l'excentricité n'est pas trop grande. Pour des ellipses de grande excentricité (très applatie), ça doit devenir moins bon.

[A voir en vidéo sur Futura]

[Drt31]

Si il est affirmé que la surface du cercle est égale S = pi * D²/4 et que celle de l'ellipse est égale S = a x b/4, a étant la valeur du grand diamètre et b = le petit diamètre de l'ellipse, on peut établir le théorème suivant :


La circonférence d'un cercle ou d'une ellipse est égale au périmètre du carré ou du rectangle circonscrit multiplié par pi/2 c'est à dire 1,57 du périmètre concerné.

Valeur mesurée en pratique sur différents format de plats oval du commerce au mm près.
Les autres formules approchées donnent des valeurs supérieures à la réalité.
Dans mon encyclopédie " Larousse ", il est affirmé que :

AIRE DE L'ELLIPSE: L'ellipse est la projection d'un cercle de rayon "a" dont le plan fait avec celui de l'ellipse l'angle 'lambda' défini par cos 'lambda' = b/a.
L'aire du cercle est égale à pi * a² ; celle de l'ellipse pi.a² x b/a = pi.a.b (affirmation de base)

[jacknicklaus]

oui, c'est une approximation bien connue. Le lien donné par coussin est très intéressant, notamment l'approximation "améliorée" proposée par Ramanujan.
Mais on ne peut pas dire :

on peut établir le théorème suivant : La circonférence d'un cercle ou d'une ellipse est égale au périmètre du carré ou du rectangle circonscrit multiplié par pi/2

car c'est une valeur approchée certes pas mauvaise, mais pas exacte.

[mach3]

La circonférence d'un cercle ou d'une ellipse est égale au périmètre du carré ou du rectangle circonscrit multiplié par pi/2 c'est à dire 1,57 du périmètre concerné.

ça ne marche pas votre truc, et si ça marchait, pourquoi on se serait fait em.. enquiquiner avec les intégrales elliptiques?

m@ch3

[Drt31]

Dans mes précipitations, je me suis trompé en affichant pi/2 = 1,57 > 1 alors que la circonférence du cercle ou de l'ellipse est inférieure au périmètre du carré ou du cercle circonscrit c'est à dire pi/4 = 0,785 < 1

En mesures pratiques, par construction et mesures effectuées à l'aide d'un centimètre de couturière, j'obtiens une valeur à 1 mm près pour une circonférence de 650 mm.

Le plus intéressant de l'ellipse est de déterminer la distance entre ses deux foyers pour pouvoir construire une voute en fonction de la largeur de celle-ci et de sa hauteur par rapport à l'axe horizontal.. il y a quelques décennies j'ai été confronté sur ce sujet où il a fallu extraire une racine carrée sans calculette ou règle à calcul..

[coussin]

Voilà le degré de précision de votre approximation en fonction du rapport des deux axes de l'ellipse.

[coussin]

J'en profite pour signaler que l'approximation de Ramanujan est étonnamment bonne, de l'ordre de 0.2% d'erreur seulement sur une large gamme d’excentricité!