Relations géométriques - Diagramme de Minkowski

[fabio123]

Bonjour,

je n'arrive pas à retrouver des relations géométriques basiques concernant un diagramme de Minkowski sur cette figure :

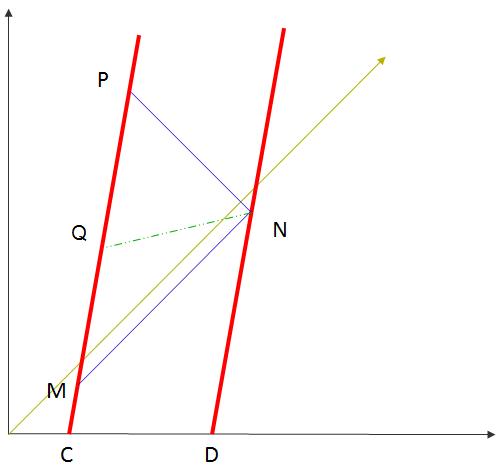
L'auteur calcule sur cette page ( http://chaours.rv.pagesperso-orange....elat/relat.htm ) la synchronisation entre 2 observateurs en mouvement (représentés par les droites rouges) par rapport au repère immobile.

Il déduit alors différentes choses que j'aimerais retrouver :

1) Le triangle MNP est un triangle rectangle, donc le triangle MNQ est isocèle.

2) En prenant l'angle theta entre les lignes rouges et la droite d'ordonnée (l'axe vertical), il trouve : angle(QMN) = PI/2 - theta

3) Enfin, l'angle theta' entre la droite QN et l'axe horizontal doit être égal à : theta' = PI/2 - angle(QNM) = theta

Questions : comment prouver 1), je me doute que c'est de la géométrie assez simple mais je bloque : pour que le triangle MNQ soit isocèle dans un triangle rectangle MNP, faut-il imposer obligatoirement que Q soit le milieu du segment [MP] ?

2) d'après ce que j'ai compris dans l'introduction de ce lien, theta représente l'angle entre la droite rouge et l'axe vertical (avec tan(theta) = v/c). Selon moi, il y a la relation de départ qui doit être : PI/2 = theta + angle(QMN) + delta ,où delta est l'angle entre la droite MN et l'axe horizontal (abscisse) :

mais l'auteur ne semble pas prendre en compte cet angle delta.

3) Comment prouver que l'angle theta' que fait la droite QN avec l'axe horizontal est égal à theta ? je n'ai pas compris la relation : theta' = PI/2 - angle(QNM)

Il y a des choses qui m'échappent, si quelqu'un pouvait m'aider. Merci
-----

[minushabens]

Q est le centre du cercle qui passe par M,N & P donc les distance QM, QN et QP sont égales. C'est dans Euclide...

[Amanuensis]

Questions : comment prouver 1)

Le milieu de l'hypothénuse d'un triangle rectangle (Q) est le centre du cercle circonscrit au triangle (à MNP).

(À suivre)

[Amanuensis]

2) d'après ce que j'ai compris dans l'introduction de ce lien, theta représente l'angle entre la droite rouge et l'axe vertical (avec tan(theta) = v/c). Selon moi, il y a la relation de départ qui doit être : PI/2 = theta + angle(QMN) + delta ,où delta est l'angle entre la droite MN et l'axe horizontal (abscisse)

On a QMN = π/4 - θ, puisque MN fait un angle de π/4 avec l'axe de ordonnées (par hypothèse)

3) Comment prouver que l'angle theta' que fait la droite QN avec l'axe horizontal est égal à theta ? je n'ai pas compris la relation : theta' = PI/2 - angle(QNM)

MQN = π - 2 (π/4 - θ) = π/2 - 2θ (parce que MQN est isocèle), et faut enlever θ pour obtenir l'angle de QN avec la verticale.

[A voir en vidéo sur Futura]

[fabio123]

ok merci, donc il y a une erreur sur l'angle QMN, c'est : angle(QMN) = pi/4 - theta

@Amanuensis : c'est l'angle de QN par rapport à l'horizontale dont l'auteur parle; je dirais :

avec angle(MQN) = pi/2 - 2 theta

et en considérant un triangle rectangle avec la droite horizontale au dessus de la droite QN :

angle(QN/horizontale) = pi - pi/2 - (pi - angle(MQN) + theta)) = pi/2 - pi/2 + 2 theta + theta = 3 theta

?? là pour le coup, je suis pas sûr, quelqu'un peut confirmer et me dire si non où est mon erreur ?

[fabio123]

Petite rectification :

angle(MQN) = π - 2 (π/4 - theta) = π/2 + 2 theta

et donc :

angle(QN/horizontale) = pi - pi/2 - (pi - angle(MQN) + theta)) = pi/2 - pi/2 + 2 theta - theta = theta

Merci

[Amanuensis]

Oui, ça corrige mon erreur de signe dans le message #4.