Somme de l'énergie dans une rotation

[yy527]

Bonjour,

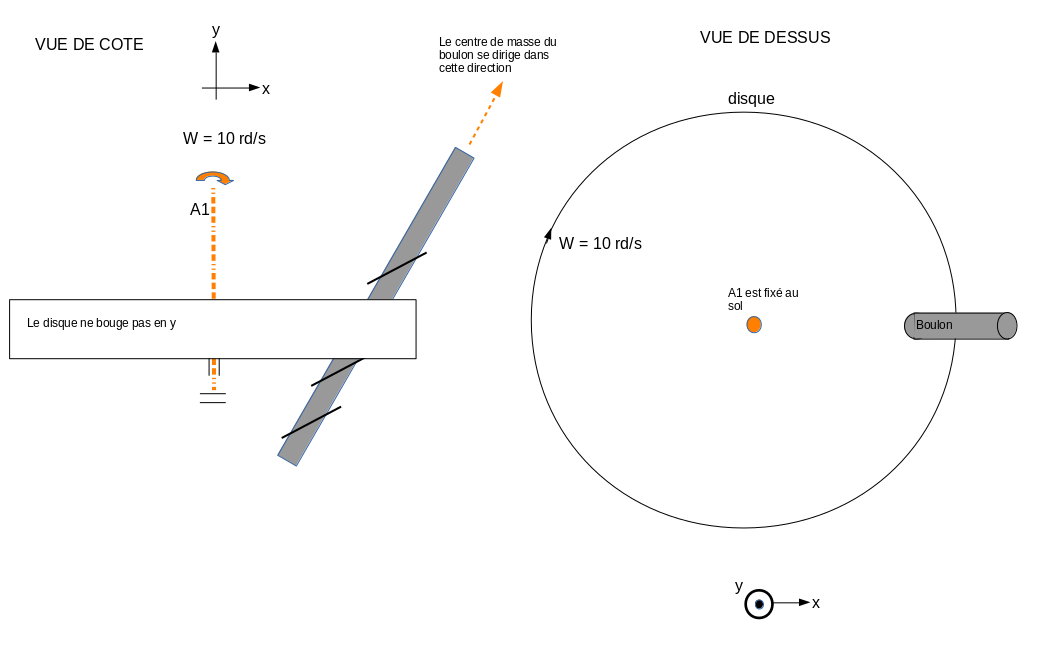
Je cherche à comprendre où se situe mon erreur de raisonnement. Il n'y a pas de gravité externe. Je prends un disque en rotation autour d'un axe A1 fixé au sol, à l'intérieur de ce disque se trouve un écrou fixe sur le disque (ou une hélice) avec une masse. Dans cet écrou passe un boulon (le boulon traverse de part en part le disque) qui ne tourne pas autour de lui même. C'est important le boulon ne tourne pas autour de lui même au début. Si on se place sur le disque, on voit le boulon tourner dans le sens inverse du sens de la rotation du disque. Je suppose qu'on est en régime continu, je passe le régime transitoire où le boulon bouge et doit accélérer son centre de masse. Il y a :

- un couple sur le disque qui tend à le freiner
- un couple sur le boulon qui tend à l'accélérer
- des forces de friction qui donne de la chaleur
- une force qui tend à décélérer le centre de masse du boulon

Avec R le rayon du boulon et F la force totale de friction.

Si le boulon/écrou est vertical avec un pas à 45° par exemple alors je trouve bien la somme de l'énergie à 0. Sur un angle très faible δ, le disque perd -δRF/√2, la friction gagne +δR√2F, le boulon n'a pas le temps d'accélérer en rotation sur lui même. Le centre de masse perd -δRF/√2.


Si le boulon/écrou a un angle de 60° par rapport à l'horizontale (voir dessin) par exemple alors je ne trouve pas 0. Sur un angle très faible δ, le disque perd δRF/2, la friction gagne δ2RF, le centre de masse exige un travail de δR√3/2F, le boulon n'a pas le temps d'accélérer en rotation sur lui même. La somme n'est pas à 0. Bien entendu le centre de masse bouge, s'éloigne de plus en plus du centre du disque mais je peux comparer avec et sans friction. Sans friction, je trouve bien que la somme de l'énergie se conserve et le centre de masse s'éloigne. Avec la friction, le déplacement du centre de masse est le même sans la force qui tend à le décélérer et que je compte.

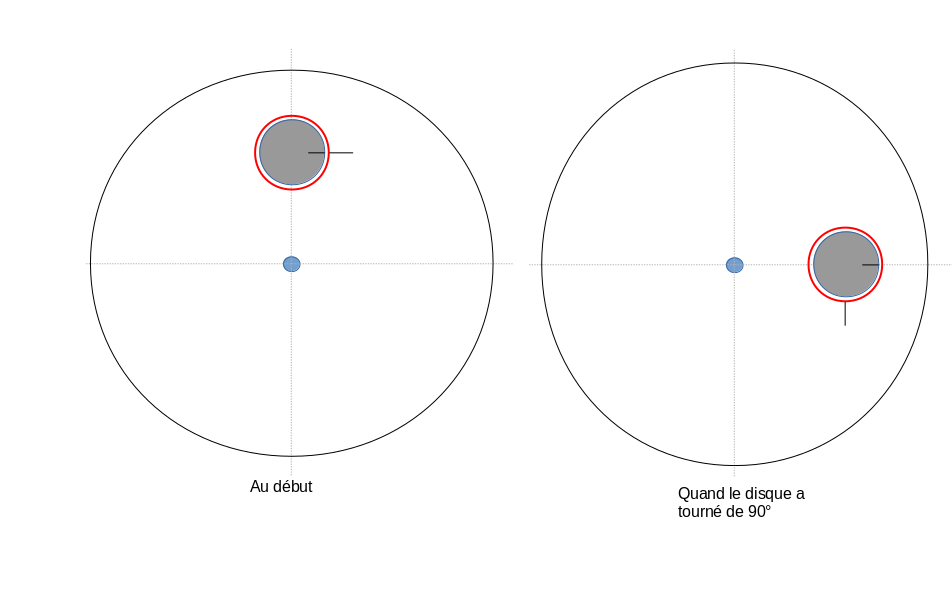
J'ai fait un dessin:



Si vous avez une idée de l'erreur ?

a+ et bonne journée
-----

[yy527]

J'ai oublié de dire que pour mes calculs, j'ai pris un pas de l'hélice à 60° sur le boulon (comme dessiné). Un tour de boulon (2piR) déplace de 2*2piR le boulon dans la direction de son axe de rotation (flèche orange en pointillés).

a+

[Amanuensis]

Si on prend à la place du boulon un tube creux fixe par rapport au disque et un piston se déplaçant librement dans le tube (avec diamètre du piston égal au diamètre intérieur du cylindre, d'où d'éventuels frottements), cela n'amène-t-il pas aux mêmes questions ? (Mais avec un système plus simple, car on élimine la rotation du piston.)

[XK150]

Bonjour ,
@ yy527
Non , la vis ( et non pas le boulon ) n'a aucune raison de tourner et de monter .
La vis veut juste s'échapper du disque tangentiellement , comme vous voulez le faire quand vous êtes dans une auto en virage .

[A voir en vidéo sur Futura]

[yy527]

@Amanuensis: ce n'est plus la même question mais globalement avec une tige sans hélice, je trouve bien la somme de l'énergie à 0. Dès que je rajoute l'hélice, je dois oublié une action quelque part.

@XK150: le boulon ne tourne pas sur lui-même mais comme le disque tourne, quand on se met sur le disque on voit tourner le boulon a w*cos(90-θ), w est la vitesse angulaire du disque et θ l'angle du boulon par rapport à l'horizontale. Comme l'écrou est fixé sur le disque, le boulon tourne par rapport à l'écrou (ou l'inverse).

[Amanuensis]

le boulon ne tourne pas sur lui-même [...] Comme l'écrou est fixé sur le disque, le boulon tourne par rapport à l'écrou (ou l'inverse).

??? Si la vis ne tourne pas sur elle-même, elle ne tourne pas par rapport à l'écrou. La rotation apparente de la vis («on voit tourner le boulon») s'applique tout aussi bien à l'écrou.

[XK150]

Pour que la vis puisse se dévisser , il faudrait qu'elle soit retenue , par exemple par un long élastique , fixée par un point extérieur au disque .
L'élastique donnerait une force dirigée à peu près dans la même direction pendant que le disque tournerait , là , oui , la vis pourrait se dévisser .
Dans votre système , non , elle ne se dévisse pas par elle-même .

[yy527]

L'écrou est fixé sur le disque, donc sur le referenciel disque l'écrou ne tourne pas, par contre le boulon tourne sur le referentiel disque car il n'est pas fixé et qu'il ne tourne pas sur lui même. Et il y a bien un dune rotation du boulon. Je l'ai testé avec un logiciel de simulation l'année dernière. La formule de la vitesse de rotation du boulon relativement au disque est -w*cos(pi/2-pi/3).

[Amanuensis]

La vis est vue tournante dans le référentiel, elle ne tourne pas plus que le pas de vis de l'écrou.

[Sethy]

Quelques situations, qui me semblent intéressantes pour approcher une solution :

1) Si on imagine la vis au centre et située sur l'axe de rotation (et donc également colinéaire avec l'attraction terrestre), est-ce que dans ce cas, elle bougerait (en tenant compte du frottement sur le pas) ?
2) Si on imagine maintenant la vis perpendiculairement à l'équateur (hé hé), donc totalement horizontale et subissant une force quasi horizontale également (en négligeant cette fois la pesanteur), bougerait-elle ?
3) Entre les deux, n'y aurait-il pas un effet semblable à celui du pendule de Foucault ?

[yy527]

La vis est vue tournante dans le référentiel, elle ne tourne pas plus que le pas de vis de l'écrou.

Non, et voici un exemple avec le disque qui tourne de 90°, le boulon ne tourne pas (en gris). L'écrou (rouge) tourne avec le disque. J'ai dessiné un trait fixe sur l'écrou et un trait fixe sur l'écrou pour montrer qu'il y a bien un décalage. Le trait du boulon est toujours à l'horizontale par contre le trait de l'écrou est passé de horizontal à vertical. Il y a bien une rotation de l'un par rapport à l'autre. J'ai dessiné le disque un peu ovale pour montré qu'il a tourné. J'ai attaché l'écrou au disque et ensuite j'ai fait tourné.

[XK150]

Pour obtenir la situation du dessin , il ne faut aucun frottement entre la vis et son écrou .
Ce qui est contraire au fonctionnement du système vis - écrou , basé sur le frottement .
Alors , il faut choisir , mais ne pas prendre un cas ou l'autre quand ça vous arrange .

[yy527]

Je ne prends pas l'un ou l'autre comme cela m'arrange. J'ai pas dit que la friction était telle que cela revenait à une soudure du boulon sur l'écrou. J'ai fait la comparaison sans friction pour dire que le centre de masse bouge aussi dans ce cas et que l'énergie se conserve. Avec une friction non nulle, il y aura une rotation entre l'écrou et le boulon, si la friction est importante alors la rotation ne durera pas longtemps. Si la friction permet une rotation pendant 1 ou plusieurs tours entre le boulon et l'écrou, je peux regarder sur 0.01° la somme de l'énergie, cela ne permet pas au boulon d'accélérer pendant assez longtemps pour négliger son énergie de rotation sur lui-même et surtout pour prendre comme quasi constante la difference de vitesse entre l'écrou et le boulon, et je regarde les autres énergies. Il ne reste pas grand chose, le couple sur le disque, la chaleur par friction et la force sur le déplacement du centre de masse.

[XK150]

Le passage de la figure 1 à la figure 2 est impossible s'il y a des frottements entre la vis et l'écrou , comme dans notre monde .

[yy527]

C'est parce que vous faites l'analogie avec une vis reelle, d'une, j'ai indiqué pas de gravité externe et de deux je n'ai pas besoin de 10 tours de l'helice en contact entre le boulon er l'écrou. Ensuite, l'image est en réponse à Amanuensis qui affirme que rien ne tourne du boulon par rapport à l'écrou. En outre, on peut choisir des matériaux avec un coefficient de friction très faible en céramique par exemple. Votre message me rappelle un cours de physique en 4°, le prof disait quesans frottement le bateau avance indéfiniment, j'avais dit que c'était pas possible et il m'a dit si regardez la somme des forces, il n'y a pas de friction. J'avais eu quelques difficultés à 'admettre...

[XK150]

Tout le monde sait ici qu'un bateau avance indéfiniment sans frottement , idem une auto sans moteur , ou une balle de tennis …
Libre à vous de faire de la physique d'un autre monde , avec des frottements , oui mais trop !

[Amanuensis]

On ne fait pas tourner une tige filetée engagée dans un écrou en tapant dessus longitudinalement (1). La raison n'est pas seulement les frottements, mais l'absence de couple. Une vis transforme un couple en force longitudinale, mais ce n'a pas l'air réversible.

L'accélération centrifuge donne une force longitudinale et un couple, mais ce dernier est dans l'axe perpendiculaire au plan radial (le plan contenant l'axe du disque et l'axe de la vis). Ce couple ne contribue qu'à coincer la vis, pas à la faire tourner par rapport à l'écrou.

(1) Avis donc aux bricoleurs du dimanche: faut utiliser un tournevis, pas un marteau.

[albanxiii]

C'est parce que vous faites l'analogie avec une vis reelle, d'une, j'ai indiqué pas de gravité externe et de deux je n'ai pas besoin de 10 tours de l'helice en contact entre le boulon er l'écrou. Ensuite, l'image est en réponse à Amanuensis qui affirme que rien ne tourne du boulon par rapport à l'écrou. En outre, on peut choisir des matériaux avec un coefficient de friction très faible en céramique par exemple. Votre message me rappelle un cours de physique en 4°, le prof disait quesans frottement le bateau avance indéfiniment, j'avais dit que c'était pas possible et il m'a dit si regardez la somme des forces, il n'y a pas de friction. J'avais eu quelques difficultés à 'admettre...

Vous voulez raisonner sur un système mécanique dans lequel on n'a ni gravité, ni frottement. Cela n'est plus de la physique, on ferme avant d'aller trop loin dans l'ésotérique.