Déplacement d'une passerelle sur rail oblique

[invited8b9b350]

Bonjour à tous !

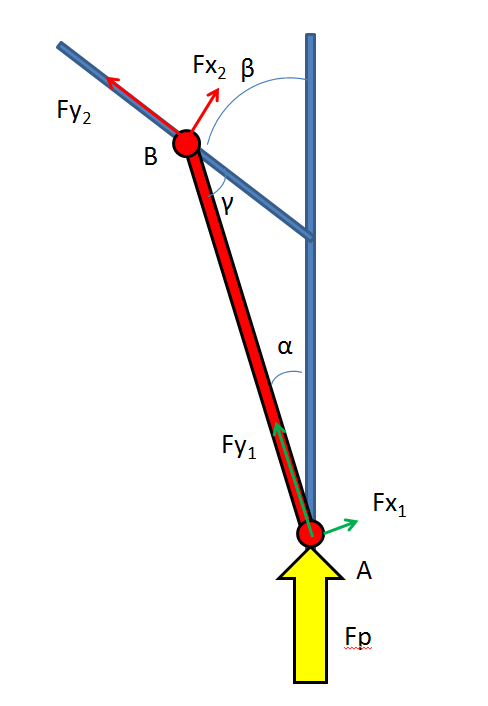
Dans le cadre d'un projet d'école d'ingénieur je dois dimensionner un moteur électrique pour déplacer une passerelle (barre rouge sur le schéma) sur des rails.

La passerelle repose sur 2 chariots à galets aux points A et B.

La répartition de la charge est de 25% sur le point A (P1) et 75% sur le point B (P2).

Le chariot posé sur le rails d'angle Beta possède aussi des galets horizontaux pour avoir du roulement au lieu de frottement.

Le but est de trouver l'effort de poussée Fp en fonction de l'angle alpha.

J'ai fais le calcul suivant mais je ne suis pas sur de ma démarche :

Condition de roulement :

Fp > muP1 + muP2sin(alpha)cos(gamma)
Fx2 = Fpcos(alpha)sin(gamma)

du coup je ne sais pas comment gérer ce Fx2

Si quelqu'un à une idée sur ce calcul je suis preneur !

Merci d'avance à tous ceux qui liront le post =)
-----

[le_STI]

Salut.

J'ai fais le calcul suivant mais je ne suis pas sur de ma démarche :

Condition de roulement :

Fp > muP1 + muP2sin(alpha)cos(gamma)
Fx2 = Fpcos(alpha)sin(gamma)

Peux-tu nous donner le détail des calculs qui t'amènent à ces équations?

Quelque chose cloche sur ton schéma : peux-tu représenter le repère (x,y,z)? Que penses-tu alors de ta représentation des composantes des forces F1 et F2?

Sur le principe : j'imagine que ce schéma est une vue de dessus du système et que la gravité s'applique sur l'axe Z, c'est ça?

[invited8b9b350]

En effet c'est une vue de dessus et la gravité suit l'axe Z

Pour ce qui est du repère, la force Fp en jaune est en y pur
Le détail du calcul est le suivant :

muP1 est la résistance au roulement sur le chariot 1

muP2sin(alpha)cos(gamma) est la résistance au roulement sur l'axe y2 rapporté à l'axe y

Fpcos(lpah)sin(gamma) est la composante en x2 de la force Fp

Est-ce la que j'ai fait une erreur ?

[le_STI]

Tu travailles donc dans 3 repères différents? C'est assez peu pratique.

Lorsque je te demandais le détail des calculs, je voulais dire : qu'est-ce qui te permet d'affirmer que Fp > muP1 + muP2sin(alpha)cos(gamma) et Fx2 = Fpcos(alpha)sin(gamma) ? Quel est le raisonnement et les calculs qui mènent à ces équations?

[A voir en vidéo sur Futura]

[invited8b9b350]

Alors en fait mon raisonnement (j'ai changé quelques points) est le suivant (j'écrit a pour alpha et g pour gamma):

Je sais qu'il me faut un effort de muP2 suivant y2 et de mup1 suivant y pour faire avancer ma passerelle (résistance au roulement)

je reporte muP2 sur l'axe y1 : muP2cos(g) (j'avais fait une erreur ici en mettant sin(g)

Je reporte ensuite cet effort sur y : mup2cos(g)cos(a)

Ainsi je pose Fp > muP1 + muP2cos(g)cos(a)

Cet effort induit une réaction suivant x2 de valeur Fpcos(a)sin(g) (reporté sur l'axe Y)

Je pose enfin Fp > muP1 + muP2cos(g)cos(a) + Fpcos(a)sin(g)


D'ou j'obtient enfin : Fp > (muP1 + muP2cos(g)cos(a)) / (1-cos(a)sin(g))

j'ai enfin tracé la courbe Fp = f(y), ou y est le déplacement, et j'obtient une courbe dégressive (ce qui me parait assez logique)

Qu'en pensez vous ?

[le_STI]

Alors en fait mon raisonnement (j'ai changé quelques points) est le suivant (j'écrit a pour alpha et g pour gamma):

Je sais qu'il me faut un effort de muP2 suivant y2 et de mup1 suivant y pour faire avancer ma passerelle (résistance au roulement)

Jusque là OK.

je reporte muP2 sur l'axe y1 : muP2cos(g)

Là ça ne va plus.
Si tu me donnes la raison pour laquelle tu projettes cette force sur y1, tu devrais trouver où est l'erreur.

Ce que j'essaye de faire de puis le début, c'est de te forcer à avoir une approche plus rigoureuse qui te permette d'éviter ce genre d'erreur.

Dans le cadre d'un projet scolaire, la rédaction d'une note de calcul en bonne et due forme me parait judicieuse (données, hypothèses, principes appliqués, calculs détaillés, solution).
Lorsque tu seras assez à l'aise avec la résolution de ce genre de problème, tu pourras certainement te passer de tous ces détails intermédiaires (bien que tu le feras tout de même de tête).

[invited8b9b350]

Et bien je projette cette force sur y1 pour ensuite la ramener sur l'axe de mes rails car ma force de poussée sera sur ce même axe, comment faire pour connaître l'incidence de cette force sur le rail Y si ce n'est en la projetant ?

[le_STI]

Je n'arrice pas à te mener où je voulais...

J'essayais de te faire comprendre qu'il faut que tu appliques le PFS et le principe d'action-réaction sur les différentes parties de ton ensemble pour pouvoir déterminer la force Fp.

On ne projette pas des forces au hasard d'un bout à l'autre du système. La projection découle seulement des deux principes ci-dessus.

D'ailleurs Fx2 et Fy2 n'ont pas les bonnes proportions.

Je te donne la première étape de résolution sous forme d'une question : On isole le chariot situé en B. Quel est le rapport entre la force de résistance au roulement exercée sur le chariot en B, la force "latérale" qu'il subit de la part du rail et la force qu'il subit de la part de la passerelle? (hypothèse : ces trois forces se croisent en B)

[invited8b9b350]

Alors du coup sur le chariot B j'ai fait la chose suivante :

(en vecteurs) : P2 + Fr + Fp (force de poussée venant de la barre rouge) + R = 0

sur x2 : -Fpsing + Rx2 = 0 => Rx2 = Fpsing
sur y2 : Fpcosg - muP2 = 0 => Fp = muP2 / cosg
sur Z : -P2 + Rz = 0 => Rz = muP2

Mais ensuite si j'isole le chariot A :

(en vecteur) : Fp (force de poussée sur y) + R (reaction sur y1) + P1 + Fr = 0

sur x : Rsina = 0
sur y : Fp - Fr - Rcosa = 0
sur z : -P1 + Rz = 0

Mais du coup je trouve R=0, je ne comprend pas :/

[le_STI]

Pourrais-tu expliciter les différentes forces s'il te plait?

J'ai un doute sur ce que sont Fr et Rx2 par exemple.

Il faudrait aussi que tu expliques pourquoi tu peux écrire que la composante en X2 du vecteur Fp peut s'écrire Fp*sin(g). A ce stade de la résolution, rien ne te donne l'orientation de Fp. (et si, par exemple, on avait un moment autour de Z appliqué sur la passerelle ?)

[invited8b9b350]

Alors Fr est la force de résistance au roulement en B (muP2) et Rx2 est la composante x2 de la réaction (que je considère normale au rail, est-ce juste ? )

Enfin j'écrit Fpsin(g) car la force de poussée est coincidente avec la barre rouge non ?

Pour ce qui est du moment je ne pense pas qu'il y en ai car les liaisons A et B sont des pivots

[le_STI]

.... la force de poussée est coincidente avec la barre rouge non ?

Tu vois, ce qu'il faudrait que tu fasses c'est réellement poser toutes les équations en isolant chaque composant un par un et en lui appliquant le PFS, et là tu n'auras plus aucun doute.

C'est comme pour le signe des composantes sur X et Y : tu as mis des "-" devant certaines composantes, mais en réalité ça découle de la somme vectorielle du PFS (somme des forces = vecteur nul et somme des moments = vecteur nul).

Je comprends que tu veuilles aller plus vite en faisant des raccourcis, mais j'ai l'impression qu'il vaudrait mieux que tu détailles l'ensemble des étapes.

Evidemment je pourrais te donner le résultat directement ou encore je pourais simplement vérifier que les équations que tu poses sont correctes, sans savoir d'où elles viennent, mais ce serait moins pédagogique.

Fr devient Rx2 => ça porte à confusion avec R (qui, si j'ai bien lu entre les lignes, est la réaction au poids?)

[invited8b9b350]

Ok je vais essayer ... mais faut il décomposer en 3 systèmes, A , B et barre rouge ou en 2 A et B ?

La grosse question que je le pose est : est ce que la résistance au roulement fait partie de la résistance R ou est ce une force à part ?

En fait si j'isole B par exemple quel bilan des forces est juste ? (équations en vecteurs) :

1) Fp(B) + R(B)+ P(B) = 0
2) Fp(B) + R(B) + Fr(B) + P(B) = 0

Fp(B) est une inconnue je pense ( ou est ce la projection de Fp(A) sur y1 ? )

Par contre je pense que je connais la composante Y de R(B) qui doit etre muP(B)

Même interrogation si j'isole A :

1) Fp(A) + R(A) + P(A) = 0
2) Fp(A) + R(A) + Fr(A) + P(A) = 0

Si je suis dans le cas 2), puis je dire que R(A) est orientée selon l'axe de la barre rouge ?

[le_STI]

Si on écrit ça sous forme vectorielle, mon choix personnel serait de prendre en compte un vecteur par interface :
-Une force F(P->B) qui regroupe donc toutes les intéractions entre la passerelle et (B)
-Une force R(B) qui regroupe toutes les forces d'intéraction entre le rail et (B)

Pour commencer, on ne sait rien sur leurs composantes. On les notera donc simplement F(P->B)x, F(P->B)y, etc...

Ensuite on pose les hypothèses simplificatrices :
Problème plan = pas de force sur z, des moments seulement autour de z.
Liaison pivot entre la passerelle et le chariot = pas de moment transmissible
Liaison glissière entre le chariot et le rail = ...

Ensuite tu appliques le PFS (somme vectorielle des forces=0, somme vectorielle des moments=0)

Tu y intègres les données (poids et résistance au roulement connus en norme et orientation).
A ce moment là, tu n'auras pas assez de données pour résoudre le système d'équations (parce que l'orientation de Fp(B) est inconnue).

2ème étape: tu isoles la passerelle.

2 forces F(A->P) et F(B->P) (tu noteras que ce sont les réactions de F(P->A) et F(P->B))

Hypothèses silmplificatrices, PFS, données, ...
Là tu trouveras l'orientation de F(A->P) et F(B->P) =>Tu pourras résoudre le premier système d'équations.

3ème étape : tu isoles le chariot (A)

Hypothèses, PFS, ... => Ton problème sera résolu

[invited8b9b350]

Donc si je comprend bien lorsque j'isole B j'ai :

/x : F(P->B)x + R(B)x = 0
/y : F(P->B)y + R(B)y = 0
/z : F(P->B)y * D + M(GlissièreB) = 0

J'isole la passerelle :

/x :F(B->P)x + F(A->P)x = 0
/y : F(B->P)y + F(A->P)y = 0

J'isole A :

/x : F(P->A)x + R(A)x = 0
/y : F(P->A)y + R(A)y = 0
/z : F(P->A)x * D + M(GlissièreA) = 0

Mais du coup les résistances au roulement sont comprises dans R(B) et R(A) ?

[invited8b9b350]

J'ai fais tout les calcul mais au final je ne trouve rien dépendant de l'angle alpha, est ce normal ?

[le_STI]

Mais du coup les résistances au roulement sont comprises dans R(B) et R(A) ?

Oui. Tu connais leur norme et leur orientation, ce qui te permettra de résoudre certaines équations (et c'est lors du passage d'un repère à un autre qu'apparaitront les termes en cos() et/ou sin() ).

/x : F(P->B)x + R(B)x = 0 oui
/y : F(P->B)y + R(B)y = 0 oui
/z : F(P->B)y * D + M(GlissièreB) = 0 non


J'isole la passerelle :

/x :F(B->P)x + F(A->P)x = 0
/y : F(B->P)y + F(A->P)y = 0
et les moments autour de z?

Tu fais une fois encore un raccourci et tu n'appliques pas le PFS dans sa totalité, en plus d'introduire une variable dont j'ignore la signification.
Je te conseille de trouver un cours sur l'application du PFS et de suivre toutes les étapes rigoureusement. Tu y es presque.

Désolé mais ce sujet est trop chronophage pour moi, je passe la main...