
- Forum
- Futura-Sciences : les forums de la science
- MATIERE
- Physique
- Le rendement de Carnot
Le rendement de Carnot
- 05/01/2019, 18h54 #91Sethy
- Date d'inscription
- juillet 2008
- Âge
- 59
- Messages
- 4 548
Re : Le rendement de Carnot
------

- 05/01/2019, 20h20 #92yvon l
- Date d'inscription
- janvier 2017
- Localisation
- sud belgique
- Âge
- 82
- Messages
- 1 470
Re : Le rendement de Carnot
Bravo, j'obtiens le même résultat en utilisant le fichier xls en #64
- 06/01/2019, 18h54 #93invite7d69d1b3
- Date d'inscription
- janvier 1970
- Messages
- 79
Re : Le rendement de Carnot
@ Sethy
Encore que je ne comprenne pas bien le sens des Q= ?
J'ai pris Q=PV
- 12/01/2019, 18h46 #94invite7d69d1b3
- Date d'inscription
- janvier 1970
- Messages
- 79
Re : Le rendement de Carnot
Bonsoir
Prenons une source chaude à température T1 et une source froide à température T2 La pression de la source chaude est P1 et celle de la source froide est P2.
Nous avons T1/T2 = k = P1/P2.
Si une masse de fluide prise à la source chaude est détendue adiabatiquement jusqu'à la température de la source froide, la pression finale atteinte (en écrivant G pour gamma) est :
Pf = P2 / k puissance (1/G-1)
G-1<1 1/(G-1)>1 k>1
donc k puissance (1/G-1) >1
et Pf<P2
- 12/01/2019, 23h14 #95Sethy
- Date d'inscription
- juillet 2008
- Âge
- 59
- Messages
- 4 548
Re : Le rendement de Carnot
Cette relation est rarement vérifiée car elle présuppose qu'on travaille à Volume constant (logique puisque P/T = nR/V et que si on pose que P/T = k, alors nR/V doit être constant or comme ni R, ni n ne varient, il faut que V reste constant).
Or dans le cycle de Carnot, aucune transformation n'est isochore (V constant), ni les transformations isothermes, ni les adiabatiques.Dernière modification par Sethy ; 12/01/2019 à 23h15.

- 13/01/2019, 15h19 #96invite7d69d1b3
- Date d'inscription
- janvier 1970
- Messages
- 79
Re : Le rendement de Carnot
@ Sethy
il faut que V reste constant
Mais oui.
J’ai une source froide à température T2 et à pression P2. J’y prends une masse de fluide de volume V.
À volume constant je chauffe cette masse jusqu’àT1.
P1 V = c T1
P2 V = c T2
P1/P2 = T1/T2
- 13/01/2019, 21h43 #97Sethy
- Date d'inscription
- juillet 2008
- Âge
- 59
- Messages
- 4 548
Re : Le rendement de Carnot
Certes, mais comme on le voit très bien dans le diagramme du cycle de Carnot, aucune des transformations n'est à volume constant.
Car une telle transformation donnerait "évidemment" une droite verticale dans les diagrammes "P-V", puisque V est l'axe des abscisses.
Donc, je ne vois pas très bien ce que cette équation vient faire dans une discussion concernant Carnot puisqu'aucune des transformations du cycle n'est une isochore.
- 14/01/2019, 10h16 #98yvon l
- Date d'inscription
- janvier 2017
- Localisation
- sud belgique
- Âge
- 82
- Messages
- 1 470
Re : Le rendement de Carnot
Voir pour cela le cycle de Stirling
https://fr.wikipedia.org/wiki/Moteur_Stirling
- 14/01/2019, 14h53 #99invite7d69d1b3
- Date d'inscription
- janvier 1970
- Messages
- 79
Re : Le rendement de Carnot
@ Sethy
Certes, mais comme on le voit très bien dans le diagramme du cycle de Carnot, aucune des transformations n'est à volume constant.
Je ne comprends pas ce que vous voulez me dire.
J’ai une source chaude à température T1 et pression P1
J’ai une source froide à température T2 et pression P2.
Les deux sources sont formées du même fluide.
T1/T2 = k
Question que je me pose : «quelle est la valeur de P1/P2 ? »
À ce stade je ne parle d’aucun cycle, ni de Carnot, ni de Stirling, ni de qui que ce soit. Que vaut P1/P2 ?
Pour répondre, je prends un volume V dans la source chaude. Température T1 et pression P1.
Je prends aussi un même volume V dans la source froide. Température T2 et pression P2.
P1 V / T1 = P2 V / T2
P1/T1 = P2/T2
P1/P2 = T1/T2 = k
- 14/01/2019, 15h39 #100Sethy
- Date d'inscription
- juillet 2008
- Âge
- 59
- Messages
- 4 548
Re : Le rendement de Carnot
La vraie relation, c'est P.V/T = n.R = k.
Donc P1.V1/T1 = P2.V2/T2.
Si on fixe le rapport P1/P2, alors la seule chose qu'on peut dire c'est que :
 est fixé.
est fixé.
D'ailleurs, il suffit de faire le calcul sur deux points du cycle de cette discussion car si la relation que tu avances est vraie, elle doit forcément vérifier n'importe quel point en général, donc les points du cycle de Carnot en particulier.
Prenons les points A et C.Bonjour.
Voici un cycle avec gamma = 5/3
Pièce jointe 380706
https://forums.futura-sciences.com/a...le-g-1-666.jpg
Ta = 600K, Tb = 300K
Pa = 2, Pb = 0,354
Va = 1, Vb = 2,828
Ici, Pa/Pb = 2 / 0,354 = 5,6 alors que Ta/Tb = 600/300 = 2 ...
Par contre, effectivement : 600/300 * 2,828/1 = 5,6.
- 14/01/2019, 16h56 #101yvon l
- Date d'inscription
- janvier 2017
- Localisation
- sud belgique
- Âge
- 82
- Messages
- 1 470
Re : Le rendement de Carnot
Dans un cycle tel que Carnot, on met une quantité de gaz donné, emprisonné dans un volume donné (mais variable), une fois en contact avec une source chaude, et une fois, ce même gaz est en contact avec une source froide. Quand le gaz est suffisamment longtemps en contact avec une des 2 sources, sa température atteint la température de la source avec lequel il est en contact.
Donc on ne prend pas de la matière (du gaz) à la source chaude ni à la source froide, rien qu'un transfert d'énergie thermique (conduction, convection) entre le gaz emprisonné et les sources de chaleur. Dans les cycles successifs, c'est toujours le même gaz qui effectue le travail.
- 14/01/2019, 18h42 #102invite7d69d1b3
- Date d'inscription
- janvier 1970
- Messages
- 79
Re : Le rendement de Carnot
@ Sethy et yvon l
J’ai une source chaude à température T1 et pression P1
J’ai une source froide à température T2 et pression P2.
Les deux sources sont formées du même fluide.
T1/T2 = k
Question que je me pose : «quelle est la valeur de P1/P2 ? »
Ça n’a rien à voir avec un cycle quelconque ni avec un volume quelconque.
Pouvez-vous répondre à cette question ?
- 14/01/2019, 19h16 #103Sethy
- Date d'inscription
- juillet 2008
- Âge
- 59
- Messages
- 4 548
Re : Le rendement de Carnot
Très facilement, la valeur de P1/P2 = k x V2/V1.@ Sethy et yvon l
J’ai une source chaude à température T1 et pression P1
J’ai une source froide à température T2 et pression P2.
Les deux sources sont formées du même fluide.
T1/T2 = k
Question que je me pose : «quelle est la valeur de P1/P2 ? »
Ça n’a rien à voir avec un cycle quelconque ni avec un volume quelconque.
Pouvez-vous répondre à cette question ?
Il y a donc une infinité de valeurs possibles.
La formule est PV=nRT. Donc si on fixe n, il reste 2 degrés de liberté. Si on fixe encore T (par le ratio T1/T2), il reste un degré de liberté. Il faut encore fixer le volume pour qu'il n'y ait plus de degré de liberté et que la pression soit également fixée.
- 14/01/2019, 21h13 #104invite7d69d1b3
- Date d'inscription
- janvier 1970
- Messages
- 79
Re : Le rendement de Carnot
@ Sethy
La formule est PV=nRT. Donc si on fixe n, il reste 2 degrés de liberté. Si on fixe encore T (par le ratio T1/T2), il reste un degré de liberté. Il faut encore fixer le volume pour qu'il n'y ait plus de degré de liberté et que la pression soit également fixée.
Vous avez raison. J'y ai réfléchi ce soir en promenant mon chien. Il faut que je revoie ma formulation.
- 15/01/2019, 11h25 #105invite7d69d1b3
- Date d'inscription
- janvier 1970
- Messages
- 79
Re : Le rendement de Carnot
@ Sethy
Je vous ai dit hier que vous aviez raison. Je n’ai pas dit que j’avais tort. Nous ne parlions pas de la même chose.
Vous parliez d’un fluide qui évolue suivant un cycle de Carnot, avec des détentes et des compressions. Je vous parle des températures et pression des deux sources chaude et froide.
J’ai sous les yeux le carnet de la locomobile de mon grand’père. Cette machine fut mise en service en 1908. Je l’ai vu tourner pendant la guerre de 1939-1945.
Dans cette machine la source chaude est fournie par la chaudière. Cette chaudière est timbrée pour «9 kilos effectifs ». Les épreuves annuelles sont faites à "11 kg effectifs". Températures correspondantes à ces pressions effectives, exprimées en "degrés centigrades" : pour 9 kg 179°C et pour 11 kg 187°C.
La source froide est fournie par l’atmosphère. La température et la pression dépendent donc de la météo.
En fonction des conditions d’utilisation et de la météo, la température et la pression des sources peut varier. Mais ça n’a rien à voir avec le cycle de Carnot.
Le cycle de Carnot est utilisé pour comprendre ce qui se passe dans le cylindre.
Cependant je revérifierai ma formulation.
- 15/01/2019, 18h37 #106Sethy
- Date d'inscription
- juillet 2008
- Âge
- 59
- Messages
- 4 548
Re : Le rendement de Carnot
De rapport entre les sources chaudes et froides, je dirais qu'il n'y en n'a pas. Ce n'est pas parce que la pression dans une machine à vapeur varie que la t° extérieure ou la p atmosphérique sont modifiées. C'est comme pour un barrage hydroélectrique, le niveau d'eau en contrebas n'influence pas le niveau d'eau dans le barrage (mais bien évidemment la production d'électricité mais ici, par hypothèse, on ne relie pas la source chaude et la source froide puisqu'on les considère indépendantes).
Par contre, si on s'intéresse à la vapeur au contact de la source chaude, là, il existe une relation qui donne la t° d'ébullition en fonction de la pression. Elle se démontre et vaut :
log(Pvapeur) = B - A / T
Il existe un grand nombre de variantes avec plus ou moins de coefficients, coefficients qui sont propre au liquide considéré.
Pour rappel, il y a ébullition quand la tension (ou pression) de vapeur est exactement égale à la pression supporté. Pour l'eau, elle est donc de 760mmHg (1atm) à 100°C. A 20°C, cette tension de vapeur vaut environ 20mmHg (limite théorique de la performance d'une trompe à ... eau). Avec ces deux points, il est possible (2 équations à 2 inconnues) de trouver A et B.
- 15/01/2019, 21h34 #107invite7d69d1b3
- Date d'inscription
- janvier 1970
- Messages
- 79
Re : Le rendement de Carnot
@ Sethy
C'est comme pour un barrage hydroélectrique, le niveau d'eau en contrebas n'influence pas le niveau d'eau dans le barrage.
Mais ça modifie la hauteur de chute.
J’ai lancé ce fil en disant que le calcul de Carnot n’est valable que si la machine tourne dans le vide ; ou pour être plus précis si la pression derrière le piston est nulle. Si la machine baigne dans sa source froide, une partie du travail fourni par la détente adiabatique est dépensée pour repousser la source froide.
D’autre part si la détente jusqu’à la température de la source froide T2 conduit à une pression inférieure à P2, alors la détente s’arrêtera à P2 et non à T2. C’est ce que j’examine actuellement.
- 17/01/2019, 10h05 #108invite62110eff
- Date d'inscription
- janvier 1970
- Messages
- 143
Re : Le rendement de Carnot
Bonjour Celuikidiki.
Bien. Bien. Bien. Bien.J’ai lancé ce fil en disant que le calcul de Carnot n’est valable que si la machine tourne dans le vide ; ou pour être plus précis si la pression derrière le piston est nulle. Si la machine baigne dans sa source froide, une partie du travail fourni par la détente adiabatique est dépensée pour repousser la source froide.
Changeons de sujet.
Soit un bon gros moteur Diesel de bateau. Quatre temps.
Temps 1. Un des pistons est au point mort haut (volume minimum). Il vient de repousser les gaz brulés par la soupape d'échappement ouverte (temps 4). Elle se ferme. Celle d'admission s'ouvre. Le piston descend. Le volume augmente. On aspire de l'air frais.
Temps 2. Le piston arrive au point mort bas (volume maximum). La soupape d'admission se ferme et le piston remonte. En comprimant l'air frais aspiré au temps 1. Et il s'échauffe (l'air). Le piston arrive au point mort haut (volume minimum).
Là, on injecte le gazole, finement pulvérisé. Et il s'enflamme. L'air se réchauffe encore plus. Et sa pression augmente fortement. Très fortement.
Et entre le piston et le vilebrequin, il y a la bielle. Qui là encaisse toute la pression qu'elle doit transmettre au vilebrequin.
Temps 3. (temps moteur). L'air sous pression (les gaz brulés) repoussent le piston, qui pousse la bielle, qui elle fait tourner le vilebrequin.
Le piston arrive au point mort bas (volume maximum).
Temps 4. La soupape d'échappement s'ouvre, le piston remonte et évacue les gaz brulés.
On a imaginé de mettre sous pression le volume derrière le piston. Là où se trouve le vilebrequin et la bielle. Pour pouvoir réduire les dimensions des diverses pièces. La bielle en particulier qui ainsi serait soumise à moins de contrainte mécanique.
Dans le cas d'un moteur à 1 cylindre, ce volume varie. Durant les 4 temps. Il diminue (temps 1 et 3). Et il augmente (temps 2 et 4). On perd donc de l'énergie pour le comprimer. Mais on la récupère lors qu'il se détend. Le bilan est nul.
Dans le cas d'un moteur à plusieurs cylindres, quand un piston monte, un autre descend. Et ce volume est constant...................... ...........
A ma connaissance, je ne pense pas que de tels moteurs "pressurisés" aient été construits.
Bonne journée
FaissolDernière modification par mach3 ; 17/01/2019 à 10h12. Motif: ajout d'une balise QUOTE

- 17/01/2019, 10h45 #109phys4
- Date d'inscription
- mars 2009
- Localisation
- Ile de France
- Âge
- 82
- Messages
- 9 784
Re : Le rendement de Carnot
Je pense que si les constructeurs ne l'ont pas fait, c'est que ce n'était pas rentable.
Les moteurs 2 temps utilisent la face arrière du piston pour assurer la phase d'admission et transfert dans la chambre principale, mais ils ont une perte de rendement du au mélange air brulé et air admis.Comprendre c'est être capable de faire.
- 17/01/2019, 10h51 #110Sethy
- Date d'inscription
- juillet 2008
- Âge
- 59
- Messages
- 4 548
Re : Le rendement de Carnot
Ce qui est compliqué dans cet exemple, Faissol, comme d'ailleurs dans le cas de la machine à vapeur, c'est qu'en fait on a pas de cycle.
Alors oui bien sûr, le mouvement du moteur est cyclique (comme la machine à vapeur) mais du point de vue de Carnot, ce ne sont pas des cycles.
Pourquoi ? Parce qu'il manque une des quatre étape.
Dans le cycle de Carnot, lorsque le gaz est complètement détendu et chaud, il subit un refroidissement et une fois revenu à la t° de la source froide, il peut être comprimé à nouveau.
Or ici, comme tu l'expliques bien, les gaz d'échappements sont envoyés dans l'air, comme dans le cas de la machine à vapeur, la vapeur d'eau s'échappe par une des deux cheminées et au cycle suivant, c'est de l'eau fraiche qui portée à l'ébullition fait bouger les pistons.
Donc, ce n'est jamais le même fluide qui parcourt le circuit. Et donc (par exemple), des relations telles que PV=nRT ne sont pas vérifiées en tout point puisque "n" varie. Dès lors, tous les autres "ratios" (rapports) qui caractérisent habituellement la machine de Carnot sont à reconsidérer.
- 17/01/2019, 11h40 #111yvon l
- Date d'inscription
- janvier 2017
- Localisation
- sud belgique
- Âge
- 82
- Messages
- 1 470
Re : Le rendement de Carnot
Bonjour à tous,(..)
On a imaginé de mettre sous pression le volume derrière le piston. Là où se trouve le vilebrequin et la bielle. Pour pouvoir réduire les dimensions des diverses pièces. La bielle en particulier qui ainsi serait soumise à moins de contrainte mécanique.(..)
A ma connaissance, je ne pense pas que de tels moteurs "pressurisés" aient été construits.
(..)
Les moteurs stirlings industriels sont pressurisés complètement. La raison 1ere est d’augmenter la quantité de gaz qui travail dans le piston. Mais, pour satisfaire au problème que tu soulèves on met sous pression tout l’ensemble du moteur. Ce qui fait que le travail moteur est réparti sur les 2 mouvements du piston. Pendant la détente, le gaz dans le piston fournit le travail et pendant la phase de compression c’est le gaz hors piston qui fourni du travail (travail pris pendant la détende du gaz dans le cylindre (car compression du gaz extérieur au cylindre).
L’erreur de certains constructeurs amateur est de ne pressuriser que l’intérieur du cylindre. Dans ce cas, il faut un volant d’inertie beaucoup plus grand.
Voir pour détail, les interventions #13 ,#16 , #24, #88
- 17/01/2019, 11h59 #112yvon l
- Date d'inscription
- janvier 2017
- Localisation
- sud belgique
- Âge
- 82
- Messages
- 1 470
Re : Le rendement de Carnot
Oui, c’était bien le cas des locomotives à vapeur. La détente de la vapeur dans le cylindre se fait en 2 temps. Au 1er temps le tiroir injecte la vapeur dans le cylindre. Ceci correspond à la partie isotherme du cycle de Carnot. Au 2e temps l’injection cesse, et la vapeur dans le cylindre continue à se détendre en se refroidissant. Ceci correspond à la détente adiabatique
En jouant sur la "longueur" d’injection on peut changer la puissance développée par la machine.
Si la "longueur" augmente, la puissance augmente, mais le rendement diminue, car la détente adiabatique devient plus courte, donc la vapeur sort du cylindre à une température encore élevée (ne fait plus de travail).
- 17/01/2019, 14h58 #113invite7d69d1b3
- Date d'inscription
- janvier 1970
- Messages
- 79
Re : Le rendement de Carnot
@ Sethy
En partant de la locomobile dont j’ai parlé précédemment, j’ai tracé une détente adiabatique avec T1=450K T2=300K P1/P2=9
Arrivé à 300K la pression est encore de 1,69 P2.
Dans ce cas de températures et de pressions, la pression de la source froide n’empêche pas la détente d’aller jusqu’à T2. Alors la seule réduction du rendement de Carnot si le piston repousse la source froide est le travail dépensé pour repousser cette source.
Je vais y réfléchir. J’ai le temps.
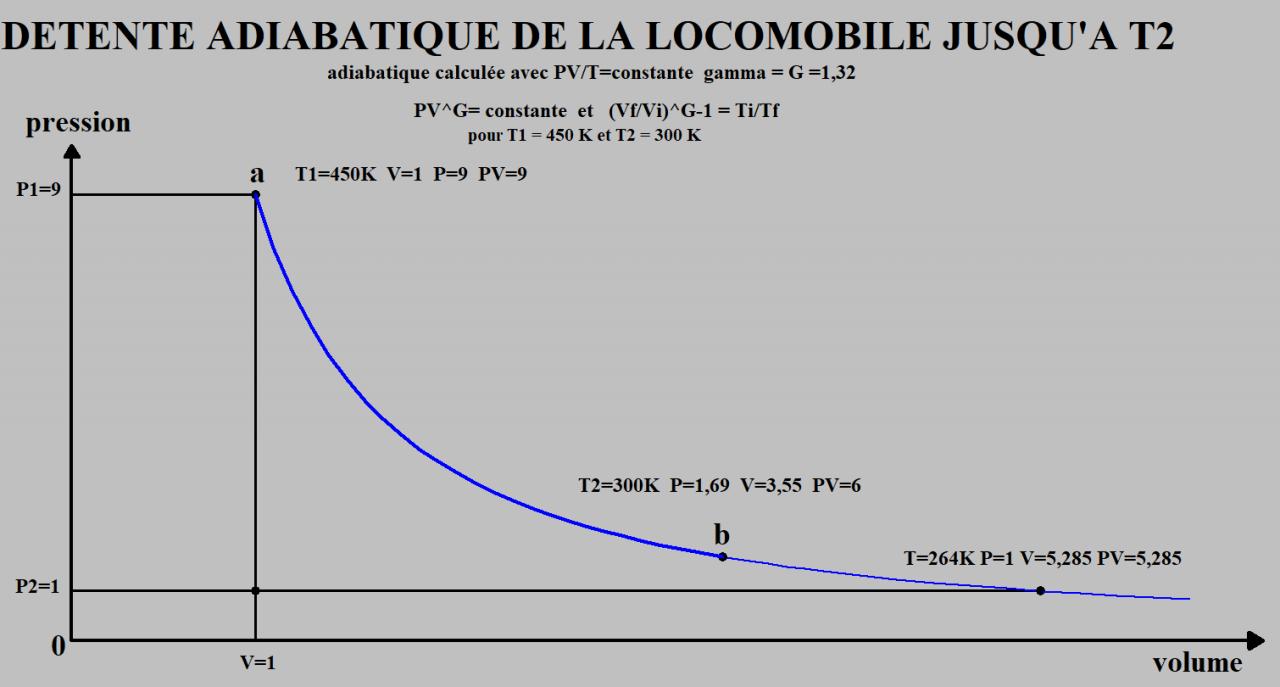

- 17/01/2019, 16h57 #114Sethy
- Date d'inscription
- juillet 2008
- Âge
- 59
- Messages
- 4 548
Re : Le rendement de Carnot
J'ai peut être fait une erreur, mais je ne trouve pas les mêmes pressions. Au point b, je trouve 3,27 et au point 2,37 au point C (264K).
Je le rappelle si Ti et Tf sont fixées, il n'y a qu'une Pf possible par Pi.
Mais plus fondamentalement, comme on peut choisir la Pinitiale qu'on veut puisque la seule chose importante c'est le rapport Pf/Pi.
Autrement dit : "jamais, jamais, jamais, la barrière des 1 atm n'aura le moindre sens pour une détente adiabatique isolée" puisqu'en imaginant une transformation qui part de 40 atm à 4, de 4 atm à 0,4 ou de 0,4 atm à 0,04, on aura toujours les mêmes résultats puisque Pi/Pf est ici toujours égal à 10".
- 17/01/2019, 19h02 #115invite7d69d1b3
- Date d'inscription
- janvier 1970
- Messages
- 79
Re : Le rendement de Carnot
@ Sethy
J'ai peut être fait une erreur, mais je ne trouve pas les mêmes pressions. Au point b, je trouve 3,27 et au point 2,37 au point C (264K).
Je vais revoir mon calcul. Quelles valeurs trouvez-vous pour V ?
Je le rappelle si Ti et Tf sont fixées, il n'y a qu'une Pf possible par Pi.
D'accord.
Mais plus fondamentalement, comme on peut choisir la P initiale qu'on veut puisque la seule chose importante c'est le rapport Pf/Pi.
D'accord.
Autrement dit : "jamais, jamais, jamais, la barrière des 1 atm n'aura le moindre sens pour une détente adiabatique isolée"
Je ne comprends pas ce que vous voulez m'expliquer.
en imaginant une transformation qui part de 40 atm à 4, de 4 atm à 0,4 ou de 0,4 atm à 0,04, on aura toujours les mêmes résultats puisque Pi/Pf est ici toujours égal à 10".
Je dis oui, mais je ne vois pas le rapport avec la Phrase précédente.
- 17/01/2019, 19h23 #116invite7d69d1b3
- Date d'inscription
- janvier 1970
- Messages
- 79
Re : Le rendement de Carnot
@ Sethy
ajout : Quelle valeur avez-vous prise pour gamma ? J'ai pris 1,32.
- 18/01/2019, 14h47 #117invite7d69d1b3
- Date d'inscription
- janvier 1970
- Messages
- 79
Re : Le rendement de Carnot
@ Sethy
Au point b, je trouve 3,27
Voici mon calcul pour Vf
(Vf/Vi)^G-1 = Ti/Tf
Avec G=1,32 Vi=1 Ti=450 Tf=300
Vf^0,32=1,5
Vf=1,5^1/0,32
Vf=3,55
Calcul pour Pf
P V^G = constante
Pour P=9 V=1 PV^G=9 et G=1,32
P V^1,32=9
P=9/V^1,32
Pf= 9/3,55^1,32
Pf=1,69
- 18/01/2019, 22h17 #118Sethy
- Date d'inscription
- juillet 2008
- Âge
- 59
- Messages
- 4 548
Re : Le rendement de Carnot
Ah oui mais non. Je suis d'accord pour le calcul de V mais après pour le calcul de P, il ne faut pas utiliser PV^gamma mais simplement PiVi = PfVf = cste.
Donc Pf = 9x1/3,55
- 19/01/2019, 10h58 #119yvon l
- Date d'inscription
- janvier 2017
- Localisation
- sud belgique
- Âge
- 82
- Messages
- 1 470
Re : Le rendement de Carnot
A mon avis, si tu considères ces valeurs, tu n'as plus de vapeur, mais de l'eau dans le cylindre. Dans ce cas la pression retombe à pratiquement 0.

- 19/01/2019, 11h01 #120Sethy
- Date d'inscription
- juillet 2008
- Âge
- 59
- Messages
- 4 548
Re : Le rendement de Carnot
Ah oui mais non, c'est moi qui me suis trompé.
Il fallait "évidemment" utilisé PV/T = cste puisque la t° varie (c'est une adiabatique, pas une isotherme).
Discussions similaires
-
Rendement de carnot et cogénération
Par ecolami dans le forum PhysiqueRéponses: 8Dernier message: 28/02/2018, 20h09 -
Rendement max de Carnot. Pourquoi ?
Par Rachilou dans le forum PhysiqueRéponses: 27Dernier message: 25/01/2013, 21h31 -
Rendement Carnot
Par invitea886451d dans le forum PhysiqueRéponses: 7Dernier message: 05/08/2011, 00h19 -
Rendement de Carnot et au delà.
Par invite231234 dans le forum PhysiqueRéponses: 22Dernier message: 06/05/2011, 16h15 -
Pourquoi on ne peut pas avoir un rendement supérieur au rendement de Carnot .
Par invite62a756ee dans le forum PhysiqueRéponses: 4Dernier message: 15/09/2010, 21h59
Fuseau horaire GMT +1. Il est actuellement 15h50.

