Le rendement de Carnot

[celuikidiki]

@ yvon l

Merci.
Je reprendrai mes graphiques avec T1=600K et T2=300K
Vous utilisez un tableur. J'utilise WINPLOT.
-----

[yvon l]

@ yvon l

Merci.
Je reprendrai mes graphiques avec T1=600K et T2=300K
Vous utilisez un tableur. J'utilise WINPLOT.

Et moi LibreOffice Calc sous Ubuntu

[Sethy]

Je me suis permis de vérifier les chiffres d'Yvon et ils sont corrects.

Les "ratios" valent tous 5,11 environ.

[yvon l]

Voila la feuille de calcul paramétrée pour tracer un cycle de Carnot.
Les données sont en gras dans le coin supérieur droit et peuvent être modifiées.
T chaude Température source chaude
T froide Température source froide
P max Pression maximum
V min Volume minimum
Vmax Volume maximum

On peut aussi changer gamma. (en B12)
Les colonnes T et U permettent de connaitre les intersections (changement de signes).
Les colonnes Q,R,T et U peuvent être agrandies par recopiage vers le haut ou vers le bas

[Sethy]

@Yvon : les fichiers excel ne seront pas validés par les modérateurs.

[yvon l]

@Yvon : les fichiers excel ne seront pas validés par les modérateurs.

J'ai remarqué qu'il y a 5 affichages du fichier !!!

[celuikidiki]

Bonne année à tous

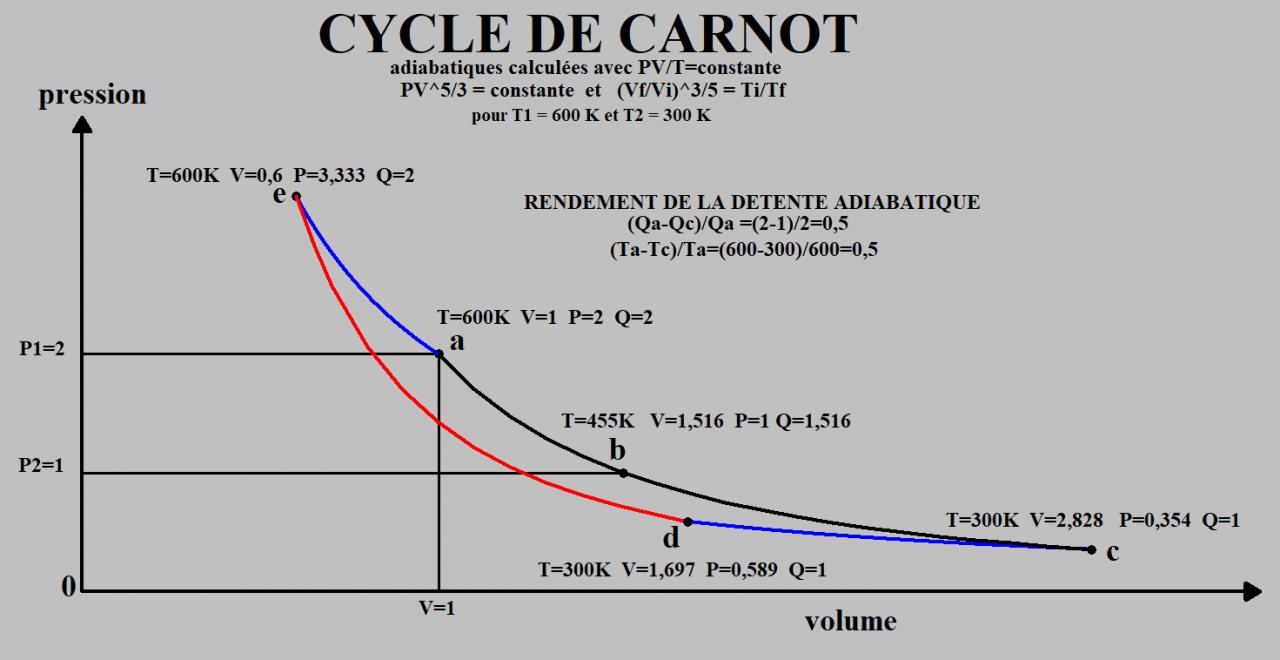
Exemple de cycle de Carnot

[ATTACH=CONFIG]380478

[celuikidiki]

Correction :
Sur le dessin précédent j'ai écrit : RENDEMENT DE CE CYCLE = 0,5
C'est faux. J'aurais dû écrire : RENDEMENT DE LA DETENTE ADABATIQUE = 0,5
Le rendement du cycle est nul.

[yvon l]

(..)

Bonjour,
Peux-tu me donner la formule que tu utilises pour tracer les adiabatiques. (Je ne retrouve pas tes résultats)
Merci

[yvon l]

Mes courbes ont l'air de coller avec ici:
http://subaru.univ-lemans.fr/AccesLi...mo/carnot.html

[Sethy]

Effectivement, en fin de détente adiabatique (point C sur le graphique), la pression doit être de 0,068 et le volume de 44.

[Sethy]

Le rendement du cycle est nul.

Heu ... à quoi sert-il alors si le rendement est nul ?

[celuikidiki]

@ Sethy

Carnot a créé ce site pour calculer le rendement de la détente adiabatique.
Les phases suivantes : compression isotherme, compression adiabatique et détente isotherme ne sont là que pour fermer le cycle et revenir à l'état initial. Les phases isothermes ne produisent rien. La compression adiabatique consomme autant d'énergie qu'en a produite la détente adiabatique.
Quand je dis que la machine de Carnot tourne dans le vide, ce n'est qu'une image. Il n'y a pas de machine. Carnot est polytechnicien ; il ne se salit pas les mains dans la graisse d'une machine. Il n'utilise que des équations. Pour comprendre, moi j'ai besoin d'imaginer une machine.

[celuikidiki]

@ yvon l
]
Peux-tu me donner la formule que tu utilises pour tracer les adiabatiques.

Tout mon calcul est fait à partir de PV/T = constante.

[yvon l]

Pour comprendre, moi j'ai besoin d'imaginer une machine

Peut-être ici:
https://forums.futura-sciences.com/c...ml#post3676223

[yvon l]

Tout mon calcul est fait à partir de PV/T = constante.

N'oublie pas que pendant les phases adiabatiques, T varie tout le temps (pas seulement V et P).
Donc, cette formule ne suffit pas

[celuikidiki]

@ Sethy

Carnot a créé ce site
Je voulais dire : ce cycle. Excusez moi.

[celuikidiki]

@ yvon l

N'oublie pas que pendant les phases adiabatiques, T varie tout le temps (pas seulement V et P).
Donc, cette formule ne suffit pas.

Effectivement en a j'ai T=600K en b T=404K en c T=300K
J'ai peut-être tort. J'essaie de comprendre.
Je vous rappelle cependant mon propos initial : la machine de Carnot tourne dans le vide.

[phys4]

Je vous rappelle cependant mon propos initial : la machine de Carnot tourne dans le vide.

Vous pouvez réaliser maintenant que votre propos initial ne sert à rien, puisque dans un cycle le volume ne varie pas.

[Sethy]

N'oublie pas que pendant les phases adiabatiques, T varie tout le temps (pas seulement V et P).
Donc, cette formule ne suffit pas

Effectivement, il y a une infinité de chemins "possibles" pour aller de T=600K à T=300K puisque P, V et T peuvent varier. A chaque Température, il existe une infinité de couples PxV qui satisfont la conservation de matière.

Mais ... parmi tout ces chemins possibles, la détente adiabatique en utilise un bien précis. qui n'est fonction que du gamma du gaz, des Températures de départ et d'arrivée et d'une autre valeur qu'on peut choisir, par exemple la Pression de départ.

Dès que cette pression de départ est fixée, le chemin l'est aussi.

A toute température, la relation :



doit être vérifiée.

[yvon l]

@ yvon l

N'oublie pas que pendant les phases adiabatiques, T varie tout le temps (pas seulement V et P).
Donc, cette formule ne suffit pas.

Effectivement en a j'ai T=600K en b T=404K en c T=300K
J'ai peut-être tort. J'essaie de comprendre.
Je vous rappelle cependant mon propos initial : la machine de Carnot tourne dans le vide.

Bonjour,
1) Sur ma feuille de calcul pour une température de 404K , j'ai une pression de 1,35 et un volume de 1.
Alors que sur ton dessin en #67 en b la température est de 404K (ok) mais une pression de 1 et un volume de 1,35 (soit le contraire) ???

2) Par la machine tourne dans le vide, tu veux dire que l'axe des volumes se trouve en 0 sur l'axe des P (pression nulle = vide)?

[yvon l]

Effectivement, il y a une infinité de chemins "possibles" pour aller de T=600K à T=300K puisque P, V et T peuvent varier. A chaque Température, il existe une infinité de couples PxV qui satisfont la conservation de matière.

(..)
A toute température, la relation :



doit être vérifiée.

Pour le calcul P(V) adiabatique , il faut éliminer la température et passer par la formule :



Puis de calculer éventuellement T(V) via T= PV/nR

[celuikidiki]

@ Sethy

Effectivement, en fin de détente adiabatique (point C sur le graphique), la pression doit être de 0,068 et le volume de 44.

Sur mon dessin la pression de la source froide est de 1. Si vous trouvez que la pression en c est de 0,068 et si la machine baigne dans sa source froide, la détente s’arrêtera à P=1 et non à T=300K.

[celuikidiki]

@ yvon l

Vous pouvez réaliser maintenant que votre propos initial ne sert à rien, puisque dans un cycle le volume ne varie pas.

Je ne comprends pas. Dans mon cycle (poste 67) le volume varie tout au long du cycle.
Si vous voulez dire que l’on revient au point de départ et que le volume n’a pas changé, c’est évident puisque nous avons un cycle réversible. Le rendement de ce cycle est nul.
Le rendement de Carnot est celui de la détente adiabatique de a à c.

[Sethy]

Pour le calcul P(V) adiabatique , il faut éliminer la température et passer par la formule :



Puis de calculer éventuellement T(V) via T= PV/nR

Question de choix. Je préfère cette formulation (que j'ai trouvée ici https://thermodynamique.fr/framabook...odynamique.pdf) et qui a le mérite de relié P comme une fonction de T et qui montre bien qu'on n'a pas le choix puisqu'à une Température choisie ne peut exister qu'une seule Pression sur l'adiabatique pour un gaz donné.

Je ne dis pas que la formule que tu suggères est fausse, elle est correcte et utile pour la représentation graphique, mais la version en "température" me semble pédagogiquement plus adaptée à la discussion qui nous occupe.

[Sethy]

Bonjour,
1) Sur ma feuille de calcul pour une température de 404K , j'ai une pression de 1,35 et un volume de 1.
Alors que sur ton dessin en #67 en b la température est de 404K (ok) mais une pression de 1 et un volume de 1,35 (soit le contraire) ???

Ah ... ça c'est intéressant. Il y a peut être juste une "inversion" dans une des formules de Celuikidiki.

[Sethy]

@ Sethy

Effectivement, en fin de détente adiabatique (point C sur le graphique), la pression doit être de 0,068 et le volume de 44.

Sur mon dessin la pression de la source froide est de 1. Si vous trouvez que la pression en c est de 0,068 et si la machine baigne dans sa source froide, la détente s’arrêtera à P=1 et non à T=300K.

Il y a un problème de logique dans ton raisonnement. Je m'explique.

Le cycle de Carnot est un exercice théorique. Si tu veux une application pratique, alors tu dois surtout choisir des conditions initiales plus "compatibles" avec notre environnement. Disons que les chiffres proposés jusqu'ici iraient bien pour une machine thermique sur la Lune.

Si tu prends l'exemple d'Yvon (Tc=600K, Tf=300K), il faut que la pression avant la détente soit de 6 bars et alors la pression en fin de détente est de 1,06 bars. Il faut juste choisir une autre Pression en fin de compression isotherme (par exemple 2 bars).

J'imagine que la, tu ne vois rien à redire puisque la pression finale (1,06 bars) est supérieure à la P atmosphérique. Or c'est exactement la même machine de Carnot. D'ailleurs si elle baignait dans le vide, la Pression finale serait toujours de 1,06 bars.

Plus fondamentalement, comme tu as pu le remarquer, on ne donne aucunes unités au grandeurs et pour cause car dans toutes les formules, ce sont leurs rapports qui interviennent : P/P, V/V et T/T. Donc tant que les rapports sont préservés, on peut changer l'unité - ou autre manière de dire la même chose - appliquer un coefficient multiplicateur de son choix.

Donc on pourrait très bien dire que 0,068 sont des Tonnes/cm^2 et que ça correspond donc "en gros" à une P de 6,8 bars ...

[yvon l]

Effectivement, en fin de détente adiabatique (point C sur le graphique), la pression doit être de 0,068 et le volume de 44.

Sur mon dessin la pression de la source froide est de 1. Si vous trouvez que la pression en c est de 0,068 et si la machine baigne dans sa source froide, la détente s’arrêtera à P=1 et non à T=300K.

Le cycle de Carnot tel qu’on le décrit ici correspond à une machine (cylindre piston) plongé dans un milieu à pression nulle (le vide). L’étanchéité d’une telle machine doit être parfaite pour maintenir la quantité de gaz de travail constant. La pression du gaz varie entre une valeur Pmax et une valeur Pmin qui tend vers 0 si le volume tendrais vers l’infini.

Maintenant, si la machine est plongée dans un milieu tel que dans l’atmosphère sur terre, le piston reçoit alors une contre pression égale à cette dernière pression.
Pour le cycle de Carnot, ceci revient à décaler l’axe des volumes. Par exemple si la pression atmosphérique est de 1, la pression sur l’axe des P varie de (Pmax-1) à (-1) (-1 si le volume tend vers l’infini).
Les valeurs négativent de P sont fournies par la contre pression atmosphérique.
Dans la pratique, toute la partie du cycle se trouvant dans la zone négative correspond à une aspiration du piston (qui est poussé par la pression extérieure au moteur) (pression atmosphérique dans l’exemple). Mais cela ne change en rien la forme du cycle .

Dans l’exemple ci-dessous:
https://www.youtube.com/watch?v=_FO4sH-FLLM
On voit bien l’aspiration du piston en caoutchouc correspondant à la pression négative.
Le fait que ce soit un moteur à cycle Stirling ne change en rien au phénomène.
Petite remarque. (comment je vois la chose)
Dans l’exemple de ce moteur stirling, comme celui-ci n’est pas étanche, le fonctionnement se positionne automatiquement dans une zone ou la pression est centrée autour de 0. La surface du cycle se voit coupée en 2 par l’axe des volumes de telle façon que les 2 demi-surfaces soient égales.

[celuikidiki]

@ yvon l

Le cycle de Carnot tel qu’on le décrit ici correspond à une machine (cylindre piston) plongé dans un milieu à pression nulle (le vide).

Merci.

[celuikidiki]

Bonjour.
Voici un cycle avec gamma = 5/3