Problème de statique avec ressort

[iPhysics]

Bonjour,

me voilà bloqué sur un problème de statique dont je sais pertinemment que je suis capable de faire de multiple erreurs, je suis donc à la recherche d'une âme charitable pour m'aider. Merci d'avance et voici le problème ainsi que mon raisonnement :

Données du problème :

- Mécanisme composé de deux solides : le levier S1 et la glissière S2 ;
- Liaison rotoïde en A entre le levier S1 et le bâti s;
- Liaison prismatique d’axe entre la glissière S2 et le bâti s;
- Contact ponctuel en P (coef. frot. : f ) entre le levier S1 et la glissièreS2 ;
- Les deux solides sont reliés par un ressort de raideur k et de longueur naturelle L ;
- La glissière S2 est soumise à une force constante horizontale et orientée vers la gauche.

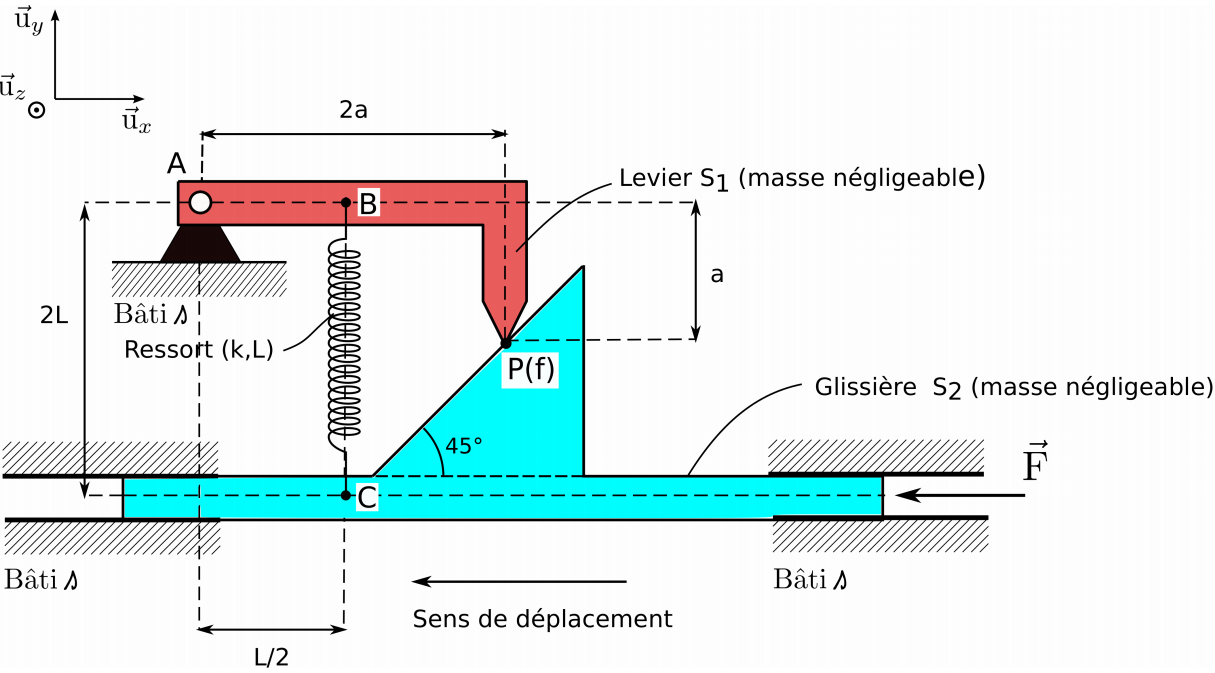
Schéma :

Pièce jointe 380625

Question :

1) Identifier toutes les inconnues de liaison
2) Calculer dans le cas où f=0 l'amplitude F de la force pour maintenir le système à l'équilibre.
3) Calculer dans le cas où f≠0 l'amplitude minimum de la force F qu'il faut appliquer sur S2 pour observer une rupture d'équilibre vers la gauche.

Raisonnement :

Question 1 : On remarque qu'il y a deux solides en cas plan, il y a ainsi un maximum de 6 équations d'équilibre indépendantes (2 pour l'équilibre de rotation et 4 pour l'équilibre de translation). Ainsi, pour que l'exercice soit soluble par la statique, il faut avoir maximum 6 inconnues de liaison.

On peut observer 2 liaisons et un contact ponctuel. Il y a une liaison sphérique qui admet deux inconnues de liaison, une liaison prismatique qui admet 2 inconnues de liaison et un contact ponctuel qui admet également 2 inconnues de liaison. Notons les

qui sont les translation selon x et y empêchées, rotation atour de z empêchée, force de liaison tangentielle et normale à la surface de contact.

Il y a 6 inconnues de liaison pour 6 équations indépendantes. Nous avons donc un potentiel système isostatique.

Question 2 :

Séparons notre raisonnement en 2 systèmes.

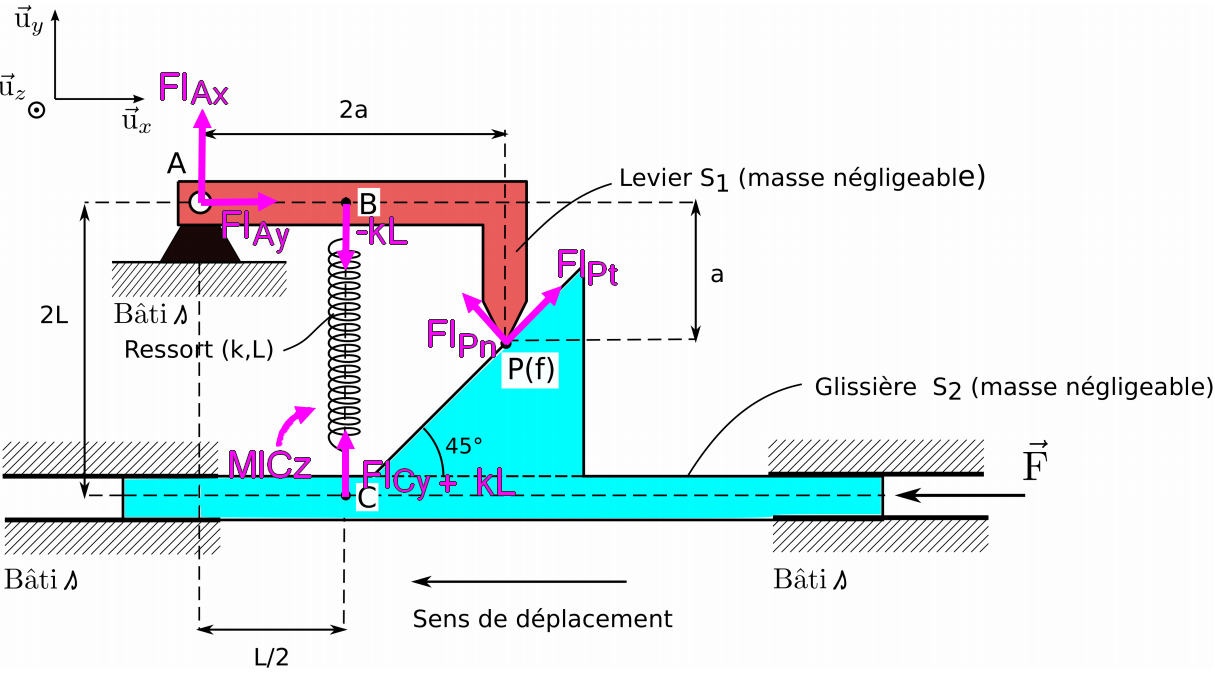
S1 :

Equilibre de translation :



avec étant donné que le ressort allongé produit une tension dans le sens de la compaction donc ici en C une tension de sens BC.
avec car le contact est sur une pente de 45 degrés d'inclinaison par rapport à l'axe x ainsi que l'axe y. (est-ce juste ?) Même raisonnement pour si ce n'est que la composante en x sera négative.

Nous allons prendre ainsi les projections selon les axes :

(1)

(2)

Equilibre de rotation : On admet l'équilibre de rotation par l'annulation du torseur des moments de force autour de l'axe z et de pôle P :

(3)

Etudions à présent S2 :

En utilsant la même méthode de projection selon les axes pour l'équilibre de translation en prenant cette fois pour compenser au niveau du contact entre les deux systèmes.

(4)

(5)

Pour l'équilibre de rotation on réutilise la méthode du torseur de moment et cette fois avec comme pôle le point C :

(6)

Maintenant que nous avons assez de relations indépendantes, penchons nous sur le réel problème.

Pour avoir l'équilibre il faut vérifier les conditions de Coulomb au point P:

Non-glissement ssi

Si f = 0, alors il nous faut Flpt = 0

ET là je ne trouve aucun moyen de m'en sortir dans les équations, dans lesquelles d'ailleurs j'ai peur de m'être trompé tant le tout est confus dans mon esprit (avec les 45 degrés pour le contact ponctuel et le sens des forces pour le ressort je ne suis pas sûr du tout).

SI quelqu'un pouvait me donner une piste.. Merci bien !
-----

[le_STI]

Salut.

La pièce jointe n'est apparement pas valide.
Tu as attaché un fichier JPG ?

[iPhysics]

Bonjour,

Je remet la pièce jointe ici :



Cette fois j'ai directement utilisé un hébergeur d'images et j'ai attaché l'URL. Sur mon premier message, j'ai importé une capture d'écran en png.

[le_STI]

Peux-tu compléter le schéma en ajoutant toutes les forces et les moments que tu as cités dans ton premier message?

Tu découvriras alors certainement une erreur sur l'orientation de FlPt.

De plus, pour le calcul de la projection de FlPt sur ux et uy, essaie d'imaginer que l'angle vaut 30° : ta formule est-elle juste? (utilisation du sinus pour projeter sur ux ???)
La formule de projection de FlPn est-elle identique à celle de FlPt au signe près? (raisonne encore une fois en imaginant que l'angle vaut 30°)

Voilà pour commencer.

[A voir en vidéo sur Futura]

[iPhysics]

Voilà un schéma qui fait l'inventaire des forces :



Si l'orientation du vecteur FlPt s'avère incorrect par son sens, je ne pense pas que cela puisse faire une erreur, étant donné que je lui donne le même sens dans toutes mes équations. La valeur que j'aurait pour FlPt serait simplement négative par rapport au sens que j'en ai donné..

Oui je suis conscient que la formule que j'ai utilisée n'est pas bonne, en effet j'ai profité d'un abus étant donné que C'est pour cela que j'utilise des sinus pour projeter sur ux. Quoiqu'il en soit je retente les forces de contact ponctuel avec la méthode classique sans raccourci.

Projetons d'abord Flpt :



Puis :



Ainsi, nous aurions ainsi que


Il va bien sûr de soi qu'avec un autre angle que celui-ci particulièrement, les formules n'auraient pas été les mêmes au signe près.. Avec un angle de 30 degrés, nous aurions eu pour les projections selon x, dans cette configuration, cos(30°)*Flpt et -Flpn*cos(60°).
L'orientation étant bien sûr subjective et où une valeur négative de Flpn ou Flpt montrerait qu'il faille la changer dans le schéma.

Le problème c'est que je ne vois pas de faille dans mon raisonnement pour ceci et cela ne change rien fondamentalement aux équations que j'ai énoncées si ce n'est qu'il faille remplacer certains sin(45°) par des cos(45°) ce qui est rigoureusement égal..

[le_STI]

Pour la question 2., tu écris

Si f = 0, alors il nous faut Flpt = 0

Mais il aurait fallu écrire "Si f = 0, alors Flpt = 0"

Du coup, tu devrais pouvoir résoudre le système d'équation après avoir corrigé l'équation des composantes sur ux des forces appliquées à S2 (de laquelle tu dois supprimer "FlCx" qui n'existe pas).
Si ce n'est pas le cas, je te conseille d'écrire l'équation des moments en A et non en P (puisque l'orientation de FlPn est connue).

[le_STI]

EDIT: Le calcul des moments en A est favorable car il permet de supprimer FlAx et FlAy de l'équation et d'introduire FlPn et FlPt, tout en sachant que cette dernière peut être exprimée en fonction de FlPn.

[iPhysics]

En effet, il s'agit d'une erreur d'interprétation de ma part, remplacer Flpt par 0 simplifie grandement les choses.

Pour le moment, je m'étais dit qu'en prenant le même pôle pour les deux systèmes cela simplifierai les choses, mais il est vrai que j'aurais dû regarder l'énoncé et me dire qu'il fallait minimiser la présence des forces de liaison en A et en C.

Le problème m'apparaît alors plutôt simple, merci !!