géodésiques radiales dans Kruskal : une erreur dans le MTW?

[mach3]

Je me suis récemment plongé dans l'étude des géodésiques radiales de la géométrie de Schwarzschild et je me suis intéressé à leur représentation dans les coordonnées de Kruskal.

En coordonnées de Schwarzchild, une telle géodésique peut se décrire ainsi :

Si la géodésique d'une particule test issue de la singularité passé, et finissant à la singularité future culmine en r=rmax, alors elle est caractérisée par les équations suivantes :





avec :
-r, la coordonnée r dans les coordonnées de Schwarzschild
-eta, un paramètre allant de -pi (singularité passée) à +pi (singularité future) et valant 0 au point culminant
-tau, le temps propre de la particule, réglé de façon à ce qu'il soit 0 au point culminant
-M, la masse du trou noir
-t, la coordonnée t dans les coordonnées de Schwarzschild, réglé de façon à ce qu'il soit 0 au point culminant
-c=G=1

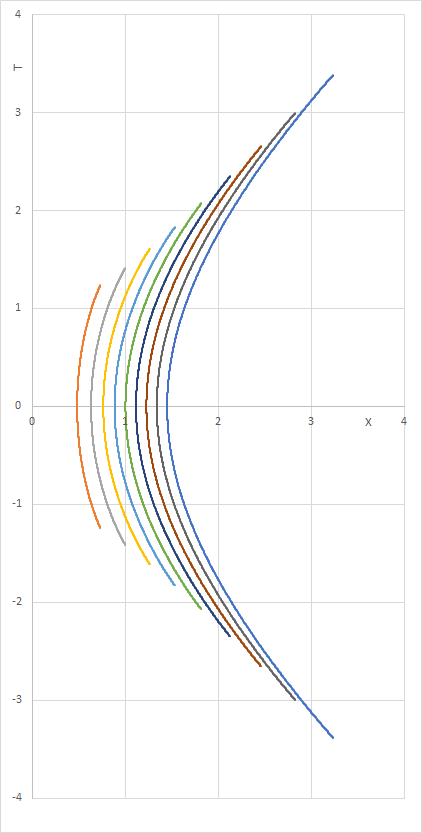
J'ai calculé quelques unes de ces géodésiques, puis j'ai entrepris le changement de coordonnées vers Kruskal-Szekeres (T,X). J'obtiens alors des courbes symétrique par rapport à l'axe T=0, telles que d²X/dT²>0 si X>0. Elles sont moins courbées que les courbes telles que X²-T²=constante (valeur de r constante), ce qui fait que le long de ces courbes, r est bien croissant depuis 0 jusqu'à rmax (en T=0) puis décroissant jusqu'à 0, comme attendu.



Mais voilà, problème. Dans la figure 31.5 de Gravitation de MTW, la géodésique radiale "F", située dans le domaine X>0, est telle que d²X/dT²<0 ! Je ne suis pas sûr pouvoir joindre cette image (droits d'auteurs), mais voici deux liens où elle est affichée :

https://askfrance.me/q/Does-someone-...se-32533063095 (vers le 1/4 de la page)
https://physics.stackexchange.com/qu...-event-horizon (vers la fin)

Cependant, par ailleurs, le site suivant montre une géodésique radiale en Kruskal telle que d²X/dT²>0 si X>0 :

https://www.mathpages.com/rr/s6-04/6-04.htm (tout en bas)

J'ai donc cherché un argument plus formel pour démêler tout ça. Messieurs Müller et Grave ont mis à disposition de tous ce joli catalogue : https://arxiv.org/pdf/0904.4184.pdf , où on trouve, tous cuits, les symboles de Cristoffel de la géométrie de Schwarzschild en coordonées de Kruskal, ce qui permet donc d'évaluer l'accélération coordonnée le long d'une géodésique radiale et de vérifier si elle est forcément orientée vers la droite, vers la gauche ou si les deux cas existent. On peut réécrire les Cristoffels que l'on trouve en page 23 ainsi :




Avec , toujours positif.

Si on écrit l'équation des géodésiques sur la coordonnée X, on a :

(on est en radial, pas de terme en theta ou phi)

Donc :

ou encore :

r' étant positif, on va s'intéresser au signe de
Si on considère le cas particulier T=0 et =0 (point culminant en T=0), alors il ne reste que :

c'est donc positif si X>0 et donc d²X/dT²>0. De plus par invariance sous rotation hyperbolique de centre X=T=0, on peut généraliser pour tout T. Donc la géodésique F du MTW serait donc fausse...

Qu'en pensez-vous?

m@ch3
-----

[Amanuensis]

Même si c'est bien le cas, cela ne change rien qualitativement: une telle géodésique «monte» (r augmente) à partir de la singularité passée (r=0), atteint un r max, puis «redescend» (r diminue) pour atteindre finalement la singularité passée (r=0).

Si c'est troublant (et si cela a amené une erreur par M, T et W), c'est juste parce qu'on a trop tendance à considérer que r=0 est la même chose que X=0 ou X petit (ce qui n'est pas le cas du tout, X peut être aussi grand qu'on veut avec r=0! Autrement dit la géodésique peut très bien se barrer à X grand (aussi bien à l'origine qu'à la fin), tout en allant à r=0).

L'apparence de la géodésique en KrSz serait alors juste un effet du choix de coordonnées.

[En d'autres termes, je ne vois pas d'objection qualitative à la forme de la géodésique telle que rectifiée.]

[mach3]

Même si c'est bien le cas, cela ne change rien qualitativement: une telle géodésique «monte» (r augmente) à partir de la singularité passée (r=0), atteint un r max, puis «redescend» (r diminue) pour atteindre finalement la singularité passée (r=0).

oui, comme je l'indique :

J'obtiens alors des courbes symétrique par rapport à l'axe T=0, telles que d²X/dT²>0 si X>0. Elles sont moins courbées que les courbes telles que X²-T²=constante (valeur de r constante), ce qui fait que le long de ces courbes, r est bien croissant depuis 0 jusqu'à rmax (en T=0) puis décroissant jusqu'à 0, comme attendu.

--

Si c'est troublant (et si cela a amené une erreur par M, T et W), c'est juste parce qu'on a trop tendance à considérer que r=0 est la même chose que X=0 ou X petit (ce qui n'est pas le cas du tout, X peut être aussi grand qu'on veut avec r=0! Autrement dit la géodésique peut très bien se barrer à X grand (aussi bien à l'origine qu'à la fin), tout en allant à r=0).

Le fait que X=f(T) soit convexe (dX/dT croissante, d²X/dT² positive) pour une géodésique radiale (avec X>0) ne me trouble pas en soi (r=f(tau) est concave de toutes façons), c'est plus le fait que M,T et W ont représenté un cas où c'est concave alors que les maths semblent dire que c'est forcément convexe (sauf erreur), donc la figure aurait été faite "à la va-vite".
Ce qui m'intéresse surtout c'est de savoir si ma "démo" est bonne (auquel cas il y a bien une erreur dans la figure), ou si je me plante quelque part et que X=f(T) peut être concave pour X>0 (il y aurait donc les deux cas possibles, concave ou convexe).

m@ch3

[Amanuensis]

Une autre manière de vérifier est d'étudier le "champ de pesanteur" pour le référentiel défini par les coordonnées de Kruskal.

Si on note U le champ des tangents unitaires des immobiles (les lignes X constant), la pesanteur est. Si la forme de la géodésique est correcte, alors on doit avoir la pesanteur orientée vers X croissant.

(Ce qui serait amusant, car on pourrait alors dire (en mauvais langage) que "dans le référentiel de Kruskal, la gravité est répulsive" ; belle leçon sur le relativisme de certains concepts... Bien entendu, cela peut être compatible avec le fait quand dans la région I et le référentiel de Schw., la gravité est attractive...)

[A voir en vidéo sur Futura]

[Amanuensis]

Ce qui m'intéresse surtout c'est de savoir si ma "démo" est bonne (auquel cas il y a bien une erreur dans la figure), ou si je me plante quelque part et que X=f(T) peut être concave pour X>0 (il y aurait donc les deux cas possibles, concave ou convexe).

J'essaierai d'appliquer mes pauvres moyens...

Par ailleurs, sur M, T et W, il y en a un vivant: tu pourrais lui envoyer un mail, fort possible que la remarque ait déjà été communiquée...

[Amanuensis]

Est-ce que cela ne pose pas un problème pour les chutes libres partant de r infini?

(Pas nécessairement, cela signifierais simplement que ces trajectoires démarrent obligatoirement avec dX/dT très négatif...)

[mach3]

Une autre manière de vérifier est d'étudier le "champ de pesanteur" pour le référentiel défini par les coordonnées de Kruskal.

Si on note U le champ des tangents unitaires des immobiles (les lignes X constant), la pesanteur est. Si la forme de la géodésique est correcte, alors on doit avoir la pesanteur orientée vers X croissant.

je mets ça à mon programme

(Ce qui serait amusant, car on pourrait alors dire (en mauvais langage) que "dans le référentiel de Kruskal, la gravité est répulsive" ; belle leçon sur le relativisme de certains concepts... Bien entendu, cela peut être compatible avec le fait quand dans la région I et le référentiel de Schw., la gravité est attractive...)

je trouve cela très amusant aussi

Par ailleurs, sur M, T et W, il y en a un vivant: tu pourrais lui envoyer un mail, fort possible que la remarque ait déjà été communiquée...

A voir. J'ai cherché un peu sur internet si il n'y avait pas un erratum qui trainerait quelque part mais en vain pour l'instant. Il est évident que si erreur il y a, je ne dois pas être le premier à la remarquer.

Est-ce que cela ne pose pas un problème pour les chutes libres partant de r infini?

(Pas nécessairement, cela signifierais simplement que ces trajectoires démarrent obligatoirement avec dX/dT très négatif...)

Sur les schémas montrant des chutes depuis l'infini en Kruskal, la géodésique part du coin inférieur droit avec un angle de presque 45° avec la verticale (exemple ici : https://www.researchgate.net/figure/...fig1_254497283 ). Ce serait à vérifier par le calcul.

m@ch3

[azizovsky]

les (r,t) que tu'as donné sont déduites d'un cas non relativiste (25,27') et (25,28)...(cycloïde)(MTW), n'ont rien avoir avec les transformations inverses des coordonnées de Kruskal (u,v).(mon opinion)

ps: ils ont la même structure que les coordonnées de Novikov.(Tome II, Fomenko,Doubrovine)

[mach3]

les (r,t) que tu'as donné sont déduites d'un cas non relativiste (25,27') et (25,28)...(cycloïde)(MTW)

non, ce sont les formules du cas relativiste, voir formules 31.10 page 824 du MTW

n'ont rien avoir avec les transformations inverses des coordonnées de Kruskal (u,v).

je ne parle pas de "transformation inverses des coordonnées de Kruskal", mais de la représentation de ces géodésiques radiales en coordonnées de Kruskal

ps: ils ont la même structure que les coordonnées de Novikov.(Tome II, Fomenko,Doubrovine)

normal, les coordonnées de Novikov sont justement conçues pour que certaines géodésiques radiales (celles qui culminent pour t=0, donc décrites par les équations du premier message) soient représentées par des droites.

m@ch3

[Amanuensis]

Sur les schémas montrant des chutes depuis l'infini en Kruskal, la géodésique part du coin inférieur droit avec un angle de presque 45° avec la verticale (exemple ici : https://www.researchgate.net/figure/...fig1_254497283 ). Ce serait à vérifier par le calcul.

Ça colle (l'angle presque à 45° signifie une vitesse-coordonnée proche de c, avec dX/dT négatif). Si cela se trouve, la vitesse-coordonnée est asymptotiquement c (ça paraît plus "logique" qu'une vitesse finie plus petite, laquelle?).

[azizovsky]

je ne parle pas de "transformation inverses des coordonnées de Kruskal", mais de la représentation de ces géodésiques radiales en coordonnées de Kruskal

m@ch3

Oui, j'ai passé une petite heure à lire pour la première fois..., mais pour arriver aux coordonnées de Kruskal, ils sont partis de la métrique de Schwarzschild avec une succession de transformations ...., jusqu'à la métrique (10,a) (page 832), mais dans Landau-Lifchitz (tome II), avec:

(1):

(2):

les relations (1) peuvent êtres transformées pour avoir la même structure que tes deux premières relations (:



il y'a une grande différence entre (10 a, MTW) et ((2), page 415, L-L) !

en plus l'intégration de donne la troisième relation (même structure).
et si tu'as des données en (u,v), comment passer à (r,t) (relations 31,18)? (tu fait l'inverse...)

[Amanuensis]

(Ce qui serait amusant, car on pourrait alors dire (en mauvais langage) que "dans le référentiel de Kruskal, la gravité est répulsive" ; belle leçon sur le relativisme de certains concepts... Bien entendu, cela peut être compatible avec le fait quand dans la région I et le référentiel de Schw., la gravité est attractive...)

Remarquons qu'au fond cela ne devrait pas être choquant: il y a des référentiels inertiels (au sens de chute libre, pas au sens galiléens), pour lesquels par définition le champ de pesanteur est partout nul. Une petite variation d'un côté ou de l'autre donnera des référentiels avec la pesanteur dans un sens ou dans l'autre, aucune raison a priori que la direction soit la même pour tous les référentiels. Cela doit même être le cas en mécanique newtonienne!

Si cela se confirme pour Kruskal, cela fait un bel exemple, auquel je me permettrai de donner une place dans un mes textes...

[mach3]

et si tu'as des données en (u,v), comment passer à (r,t) (relations 31,18)? (tu fait l'inverse...)

je pars des géodésiques décrites en coordonnées de Schwarzschild (obtenues par les formules du premier message), et ensuite je change de coordonnées de (r,t) vers (X,T) (ou (u,v), ça dépend des auteurs après, c'est (u,v) dans le MTW, mais je préfère (X,T) comme noms, sinon je n'arrive pas à me souvenir laquelle est timelike et laquelle est spacelike) et je regarde la tête des courbes et je constate que les fonctions X=f(T) qu'elles représentent sont convexes si X>0. C'est tout.

Mais peu importe, tout ça c'est secondaire, sans importance en fait et même limite hors-sujet.

La vraie question dans ce fil, c'est est-ce que dans un graphe en coordonnées de Kruskal, une fonction X=f(T) décrivant une géodésique radiale dans la partie X>0 peut être concave ou est forcément convexe, indépendamment de la formule qui permet d'obtenir X=f(T) (que ce soit directement en kruskal ou via schwarzschild), et donc la géodésique F de la figure 31.5 est elle correcte ou non.

m@ch3

[mach3]

ou encore :

r' étant positif, on va s'intéresser au signe de

pour aller un peu plus loin, on peut remarquer que le terme en facteur de r' peut se voir comme un produit de 3 matrices de la forme u^T M u (u matrice colonne, M matrice 2x2 symétrique). Pour que ce terme soit toujours positif pour tout u (donc tout et ), il faut et il suffit que M soit définie positive. On lui trouve comme valeurs propres X+T et X-T. Cette matrice est donc définie positive tant que X>0 et X²>T², ce qui couvre donc toute la région I.
Dans la région I donc, l'accélération coordonnée serait donc vers la droite pour toute géodésique radiale. Pour les régions II et IV la matrice est indéfinie, donc le sens de l'accélération coordonnée sera dépendant de u.

...

En poursuivant la réflexion, j'ai trouvé encore mieux! factorisons par :



r' est positif, , seul le signe de (avec , qui n'est autre que la vitesse coordonnée) nous intéresse. C'est un polynôme de degré 2 en V, , qu'il suffit d'étudier pour connaitre la direction de l'accélération coordonnée en fonction de l'évènement et de la vitesse coordonnée en cet évènement.

m@ch3

[Amanuensis]

pour aller un peu plus loin, on peut remarquer que le terme en facteur de r' peut se voir comme un produit de 3 matrices

Somme ?

La matrice est [[X, -T],[-T, X]], c'est ça?

[mach3]

Somme ?

non non, un produit :

m@ch3

[Amanuensis]

OK, c'est le mot matrice qui m'a égaré, je cherchais trois matrices 2x2...

[Amanuensis]

Par ailleurs, comme indiqué par MP, je trouve aisément qu'au sommet (quand dr--et dX--s'annule), l'accélération est vers la droite, ce qui infirme la courbe présentée dans le MTW.

Plus généralement, je trouve bien que la pesanteur dans le référentiel défini par les coordonnées de Kruskal est partout "répulsive" ou plus exactement centrifuge, i.e., orientée vers X² croissant.

(Cela ne permet pas de conclure pour toute la géodésique, faut prendre en compte en plus l'effet de la vitesse-coordonnée (dX/dT), qui rajoute un terme dont l'origine est similaire à celle de l'accélération de Coriolis.)

[mach3]

Ok, affaire quasiment réglée pour moi, la géodésique F serait bien tracée dans le mauvais sens dans la figure. Le seul point qui me reste à vérifier c'est les Cristofells donnés par Müller (manquerait plus qu'il y ait une erreur dedans, ça ficherait tout par terre).

J'ai contacté le Professeur Thorne, mais je ne sais pas si j'aurais une réponse. Je suppose que c'est une personne très occupée.

m@ch3