Maximum d'entropie

[Opabinia]

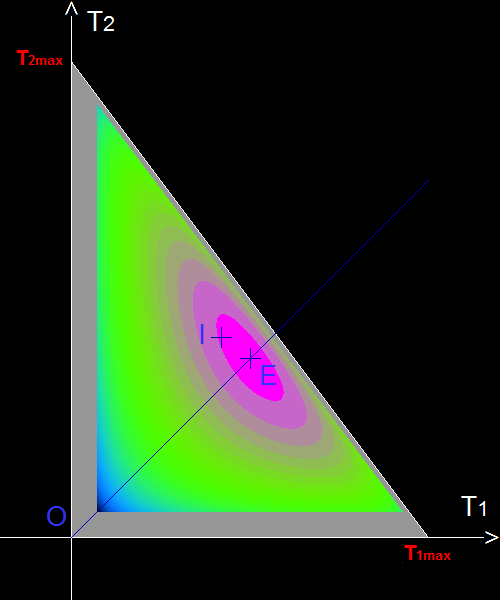
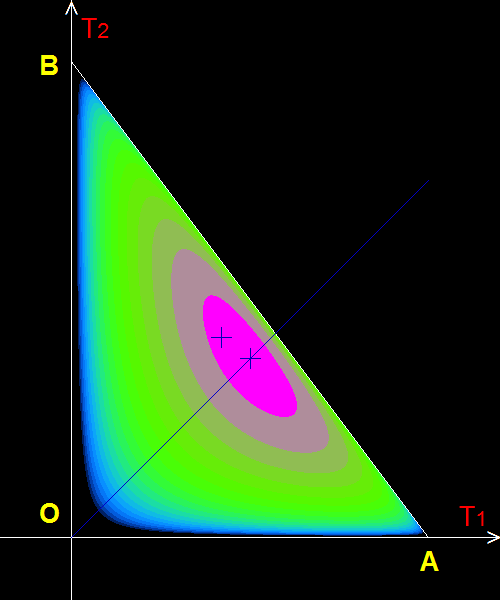
L'exemple proposé illustrait la question que tu avais posée (# 01)

Un système isolé atteint un équilibre thermodynamique lorsque son entropie est maximale, mathématiquement on écrit que la différentielle de l'entropie
dS=0 mais peut on dire aussi que les dérivées partielles de l'entropie par rapport aux variables du systèmes sont nulles aussi?

Si tu veux discuter de relations mathématiques, il faut au moins accorder un minimum d'attention aux calculs dans lesquels elles sont impliquées.

1°)

Ecrire dS=0 pour un système isolé à l'équilibre est parfaitement vraie, mais c'est pas un résultat intéressant ...

C'est au contraire la relation décisive qui permet de caractériser l'état recherché.
Voir le message (# 11) où a été établie l'expression de la variation élémentaire d'entropie:

dS = m₁C₁(1/T₁ -1/T₃).dT1 + m₂C₂(1/T₂ -1/T₃).dT₂ .

(dS) identiquement nul, c .à d. dS = 0 quelles que soient les variations (dT₁, dT₂) des températures implique entre autres:
a) pour dT₂ = 0 et dT₁ non nul: 0 = m₁C₁(1/T₁ -1/T₃).dT1 ,
ce qui conduit à m₁C₁(1/T₁ -1/T₃) = 0 d'où T₁ = T₃ ;
a) pour dT₁ = 0 et dT₂ non nul: 0 = m₂C₂(1/T₂ -1/T₃).dT2 ,
ce qui conduit à m₂C₂(1/T₂ -1/T₃) = 0 d'où T₂ = T₃ ;

2°)

PAR CONTRE dS=0 ou dU=0 (je maintiens et je signe) n'IMPLIQUE PAS la nullité des dérivées partielles de S ou de U par rapport aux variables d'état

L'égalité dU = 0) caractérise l'évolution du système, et reste vraie pour tous les états envisagés;
par contre (dS = 0) n'est vérifiée qu'en un état particulier, l'état d'équilibre recherché.

3°)

sinon on arrive aux absurdités du type T=P=0 lorsqu'on a dU=0 par exemple.

Si l'on part d'une absurdité - et la relation envisagée dU = -P.dV + T.dS en est une,
on est sûr d'être conduit à d'autres absurdités ! La démarche envisagée n'y est pour rien ...
-----

[Keisersoze]

Merci pour votre réponse, mais j'avoue que je ne comprends pas bien votre raisonnement.
Si on reprend votre point 2) (avec lequel je suis d'accord) selon lequel dU=0 pour tous les états envisagés et dS=0 n'est vrai que pour un état particulier , l'état d'équilibre, on a une relation vraie pour un point (l'état d'équilibre) et l'autre vraie pour de nombreux points (les différents états d'équilibres pour une évolution quasistatique). Pourquoi ce qui est vrai pour dS en un point ne l'est pas pour dU en tous les points ?
Prenons l'exemple d'une détente adiabatique d'un gaz dans de manière quasistatique en laissant pour chaque dV>0 se faire l'équilibre interne, on imagine donc un chemin quasistatique sur lequel on peut utiliser l'identité thermodynamique dU=-PdV+TdS (S et V étant les variables naturelles de ce problème) tout en ayant dU=0 (pas de travail pas de chaleur), dans mon cours on a dU=0 vrai en tout point de la transformation on ne dit pas que P=T=0, ça nous permet justement de calculer la variation d'entropie de la transformation on montrant qu'on dS=P/T*dV

[Keisersoze]

D'autant que je ne comprends pas bien pourquoi on aurait dS=0 quelquesoit les variations de dT1 ou dT2, si cette relation est vraie UN point alors si on appelle a le point d'équilibre on doit écrire
dS(a) = m1C1(1/T1 -1/T3).dT1(a) + m2C2(1/T2 -1/T3).dT2(a)=0

dT1 et dT2 sont des différentielles au même titre que dS, je ne vois pas bien pourquoi la relation dS(a)= 0 peut être vraie en unique point tout en prenant les variations de dT(1ou 2) comme bon nous semble.

[Opabinia]

dS = m₁C₁(1/T₁ -1/T₃).dT₁ + m₂C₂(1/T₂ -1/T₃).dT₂ = 0

dT1 et dT2 sont des différentielles au même titre que dS, je ne vois pas bien pourquoi la relation dS(a)= 0 peut être vraie en unique point tout en prenant les variations de dT(1ou 2) comme bon nous semble.

La variation élémentaire d'entropie (dS) est une combinaison linéaire des variations élémentaires de température (dT₁, dT₂ ), par l'intermédiaire de deux coefficients

m₁C₁(1/T₁ -1/T₃) , m₂C₂(1/T₂ -1/T₃)

dépendant de l'état considéré, caractérisé par les températures (T₁, T₂, T₃).
C'est justement à ces coefficients que l'on est conduit à imposer une valeur nulle, afin que l'entropie reste quasi-constante (dS = 0) au voisinage de l'état considéré (dT₁ ou dT₂ ≠ 0).
Revoir le calcul détaillé en (# 31).

[gts2]

Prenons l'exemple d'une détente adiabatique d'un gaz dans de manière quasistatique en laissant pour chaque dV>0 se faire l'équilibre interne, on imagine donc un chemin quasistatique sur lequel on peut utiliser l'identité thermodynamique dU=-PdV+TdS (S et V étant les variables naturelles de ce problème) tout en ayant dU=0 (pas de travail pas de chaleur), dans mon cours on a dU=0 vrai en tout point de la transformation on ne dit pas que P=T=0, ça nous permet justement de calculer la variation d'entropie de la transformation on montrant qu'on dS=P/T*dV

Dans une détente adiabatique réversible dU est non nul, il y a du travail fourni. Si c'est adiabatique réversible dS=0 (le même =0 que dU=0 pour un système isolé, c'est-à-dire pas un extremum, mais S=Cte).

[gts2]

D'autant que je ne comprends pas bien pourquoi on aurait dS=0 quelque soit les variations de dT1 ou dT2.

Tout simplement parce que dT1 et dT2 ne sont pas les variations de T, mais les coordonnées locales permettant d'écrire la différentielle.
Dans le cas d'une fonction d'une variable, on peut définir le "nombre" dérivée en x=x1, valeur de f'(x) en x=x1. On peut écrire l'équation f'(x)=0 pour déterminer x1 correspondant à un extremum.
Dans le cas d'une fonction de n variables, on peut définir les "nombres" dérivées en (x=x1, y=y1 ...). On peut écrire l'équation pour déterminer x1 correspondant à un extremum.
Mais comme vous l'avez vous même remarqué ce n'est pas très pratique quand il y a plusieurs grandeurs que, de plus, on ne connait pas, dS=0 condense ceci comme, là encore, vous l'avez vous-même remarqué.

[Keisersoze]

Pour ce qui est de la détente adiabatique, ne peut on pas imaginer un gaz se détendant dans un piston (sans frottement) piston lui même placé dans le vide et de telle manière que les variations de volume soient suffisamment lentes pour qu'on puisse utiliser l'identité thermodynamique dU=TdS-PdV ?
On aurait aucun travail ni bien sur de chaleur échangée, d'où dU=0.
Dans mon cours il est dit que pour que pour une détente d'un gaz dans le vide, il est possible d'imaginer un chemin quasistatique afin d'utiliser l'identité thermodynamique. Et même si c'est en pratique impossible on a tout de même le droit d'utiliser l'identité thermodynamique, nan?

[gts2]

On a le droit d'utiliser l'identité thermo entre deux points quelque soit le chemin réversible ou non, puisque c'est une relation entre fonction, il faut simplement que la fonction soit définie au départ et à l'arrivée (T et P uniformes ici).

Si un piston est soumis d'un côté à P de l'autre à zéro, il me parait difficile d'imaginer que la variation de volume soit lente.

[mach3]

Il transparait dans les échanges une confusion larvée, dont il est difficile de prendre conscience, et dont j'ai été victime pendant longtemps.

Si on écrit df=adg+bdh = 0 en pensant df, dg et dh comme des accroissements infinitésimaux, on peut tomber dans un piège : se dire que si a et b sont non nuls, il y existe des couples d'accroissements dg et dh tels que df=0. Notamment le cas où ces accroissements seraient nuls. On considère naïvement dg et dh comme des nombres (certes très petits) qu'ils ne sont pas. En fait on effectue une dérivée directionnelle, suivie d'une intégration entre deux bornes arbitrairement proches sans le savoir : on cherche un opérateur de dérivée directionnelle tel que si on lui applique dU, on obtient 0, et ceux-là on en trouve forcément, il suffit que la direction soit tangente à la sous-variété de U constant (une ligne niveau dans le cas d'une variété 2D), ou, encore plus simple, qu'il s'agisse de l'opérateur nul (cas d'un système statique, pas forcément à l'équilibre).

On raisonne sur
(la variation de étant suffisamment petite pour que a et b soient considérées comme des constantes)
est un paramètre qui caractérise le chemin suivi par le système, cela peut être le temps notamment.

Au lieu de raisonner sur


, et sont des nombres (petits certes), alors df, dg et dh ne sont pas des nombres, mais des 1-formes

df=0 signifie intrinsèquement que f ne changera pas quelque soit la direction dans laquelle on dérive. On cherche une situation où est nul quelques soient et . Cela implique la nullité de a et b. Cela ne doit pas être confondu avec qui peut se produire quand a et b sont non nuls, il suffit simplement que le chemin suivi par le système convienne, ce qui inclue la stationnarité, c'est à dire et (un système qui ne change pas au cours du temps, qu'il soit à l'équilibre ou pas).

Exemple pour un système fermé évoluant de manière réversible :

: il faut T=P=0, situation non physique, sans intérêt.
, évolution du système à énergie interne constante : T et P sont non nulles, le chemin est tel que les variations de S et V aboutissent à ce que U ne varie pas (et cela inclut une situation statique), par exemple la détente isotherme d'un gaz parfait.

m@ch3

[gts2]

Tout à fait d'accord, c'est que j'essayai de dire de manière simpliste :
"Tout simplement parce que dT1 et dT2 ne sont pas les variations de T, mais les coordonnées locales permettant d'écrire la différentielle."

[mach3]

Je pense qu'il y en effet des pb de notations, mais la thermo en est bourrée : autre exemple, quand on écrit dU=-PdV+TdS et dU=CvdT + (l-P) dV, il est évident que ce n'est pas le même fonction U (je ne sais si les variétés permettent de résoudre le problème).

L'ensemble des états est une variété, sur laquelle on défini des champs scalaires T,P,V,S... Et en chaque point de la variété (chaque etat) il y a :

-un espace vectoriel tangent qui contient les opérateurs de dérivée directionnelle (appliqué à un champ, ils donnent les dérivées directionnelles du champ). Il se définissent via l'ensemble des courbes paramétrées (le paramètre pouvant être le temps) possibles (les chemins) qui passent par cet état et auxquelles ils sont tangents.

-l'espace vectoriel dual du précédent, appelé cotangent, qui contient les applications linéaires définie sur l'espace vectoriel tangent, les 1-formes différentielles (appliquées à une dérivée directionnelle, elles donnent un scalaire)

Les espaces tangents et cotangents permettent de définir des opérateurs de dérivée directionnelle et des 1-formes en chaque point, et donc de parler de champs d'opérateur de dérivée directionnelle et de champs de 1-forme sur la variété.

Parmi ces champs de 1-formes, il y en a des particuliers, les champs de 1-formes exactes(*), que l'on construit en prenant la dérivée extérieure (d) des champs scalaires définis (appliqué à un champ scalaire, d donne simplement son gradient). On a par exemple un dU en chaque état, qui dépend de comment varie U dans le voisinage immédiat de l'état. Si on applique la 1-forme exacte dU sur un opérateur de dérivée directionnelle, on obtient la dérivée directionnelle de U (comme si on avait appliqué cet opérateur à U(**)).

La construction des champs de 1-forme exactes donne naissance, en parallèle, à des champs d'opérateurs de dérivée directionnelle particuliers, les opérateurs de dérivée partielle, qui en tout état (un opérateur en chaque état) donneront 1 si on leur applique une certaine 1-forme et 0 si on leur en applique certaines autres. Par exemple, l'opérateur de dérivée partielle par rapport à S à V constant donne 0 si on lui applique dV (c'est la dérivée de V par rapport à S si V est constant, donc c'est automatiquement nul) et donne 1 si on lui applique dS (c'est la dérivée de S par rapport à S si V est constant, donc c'est automatiquement 1).

Les champs scalaires ont des dépendances les uns par rapport aux autres, ils peuvent être lié par une équation d'état (par exemple PV=RT), par une contrainte ou par une définition. Il en résulte des dépendances entre les 1-formes exactes (par exemple RdT = PdV +VdP). En fait si on prend le nombre de champs scalaire définis et qu'on y soustrait le nombre de relations qui existent entre eux (et qui ne se déduisent pas les unes des autres), on obtient la dimension de l'espace vectoriel cotangent, qui est aussi celle de l'espace tangent et celle de la variété.

Plaçons nous dans le cas d'un système fermé se transformant de façon réversible (par exemple un gaz dans un piston). On a :

dU=TdS+PdV

On voit donc qu'on peut écrire la 1-forme dU comme une combinaison linéaire de 2 autres 1-forme (toutes les autres 1-formes, dT, dP, dH, etc, peuvent aussi s'écrire comme une telle combinaison linéaire), qui forment une base de l'espace vectoriel cotangent. La dimension de la variété est 2.

Les coordonnées de la 1-forme (les coefficients de la combinaison linéaire) dans cette base sont des dérivées partielles de U. T est la coordonnée suivant dS et -P la coordonnée suivant dV dans la base dS,dV. T est la dérivée partielle de U par rapport à S à V constant et -P celle par rapport à V à S constant. En effet, considérons par exemple un chemin de paramètre tel que S varie comme alors que V ne varie pas, alors en appliquant dU l'opérateur de dérivée directionnelle correspondant on obtiendra le coefficient situé devant dS, T, qui sera donc égale à la variation de U par rapport à , donc par rapport à S mais avec V constant.

On peut choisir ensuite d'exprimer dS en fonction de dT et dV et on obtient alors l'expression de dU en fonction de dT et dV. C'est un changement de base. C'est le même objet géométrique, dU, mais exprimé dans une base différente. Dans cette base, il a de nouvelles coordonnées, les dérivées partielles par rapport à T à V constant (Cv) et par rapport à V à T constant (l-P).

Graphiquement on peut représenter la variété correspondante à ce cas dans R3. Si on représente U en fonction de S et V ou en fonction de T et V, il s'agit de deux fonctions différentes, U(S,V) et U(T,V), l'une mettant en relation les champs scalaires U, S et V, l'autre mettant en relation les champs scalaires U, T et V. Ce sont deux représentations d'un unique champ scalaire U sur la variété. En fait on choisit simplement une représentation où dS et dV dans un cas, ou dT et dV dans l'autre, ne changent pas d'un point à l'autre de la variété : ce sont des champs uniformes (et ils forment en général une base orthogonale dans la représentation).

Un plan tangent en un point de la surface représentative de U en fonction de S et V aura comme pentes T et -P suivant les axes S et V.

(*) c'est aussi applicable aux 1-formes fermées qui dérivent de champs scalaires un peu particuliers, comme une variable angulaire, hors-sujet ici
(**) c'est un point que j'ai mis du temps à intégrer

m@ch3

[Keisersoze]

merci beaucoup mach, je pense que ça répond à nos questions, je vais mettre cette page en favori pour pouvoir y revenir et merci pour les références que vous m'avez donné sur un autre fil que je viens de remarquer à l'instant.

[Opabinia]

@ gts2 (# 40)

c'est que j'essayai de dire de manière simpliste :
"Tout simplement parce que dT1 et dT2 ne sont pas les variations de T, mais les coordonnées locales permettant d'écrire la différentielle."

(dT₁) et (dT₂) sont les variations élémentaires des températures (T₁, T₂) de deux des trois parties que comporte le système; ces températures sont aussi des variables (ou coordonnées) d'état de ce système, puisque la troisième (T₃) leur est implicitement liée.

L'intégration des relations différentielles

(1) 0 = m₁C₁.dT₁ + m₂C₂.dT₂ + m₃C₃.dT₃ ;
(2) dS = (m₁C₁/T₁).dT₁ + (m₂C₂/T₂).dT₂ + (m₃C₃/T₃).dT₃ ;

entre l'état initial caractérisé par les températures (T°₁, T°₂, T°₃) et un état quelconque ne pose aucune difficulté dans le cas de capacités thermiques constantes; on peut de plus alléger la notation en posant:

m₁C₁ = C_a.m₃C₃ ; m₂C₂ = C_b.m₃C₃

ce qui donne les nouvelles relations différentielles:

(1') 0 = C_a.dT₁ + C_b.dT₂ + dT₃ ;
(2') dS = m₃C₃((C_a/T₁).dT₁ + (C_b/T₂).dT₂ + (1/T₃).dT₃) .

1°) L'intégration de la première exprime toujours la conservation de l'énergie et fournit la relation qui intervient entre les trois températures:

(1") 0 = C_a.(T₁ - T°₁) + C_b.(T₂ - T°₂) + T₃ - T°₃ .

On en déduit
a) l'expression de (T₃) en fonction des deux autres termes:

(1a) T₃ = T°₃ - C_a.(T₁ - T°₁) - C_b.(T₂ - T°₂)

;
b) la température finale du système, atteinte lorsque l'équilibre thermique est réalisé (T₁ = T₂ = T₃ = T_f):

(1b) T_f = (C_a.T°₁ + C_b.T°₂ + T°₃)/(C_a + C_b + 1) .

2°)L'intégration de la seconde conduit à l'expression de l'entropie du système:

(2a) S = S° + m₃C₃(C_a.Ln(T₁/T°₁) + C_b.Ln(T₂/T°₂) + Ln(T₃/T°₃)) .

On a envisagé dans ce qui suit les valeurs suivantes:

C_a = 4 ; C_b = 3 ; T°₁ = 300 K; T°₂ = 400 K; T°₃ = 456 K;

ce qui entraîne: T_f = 357 K ;
la température thermodynamique (T₃) étant par ailleurs positive , les deux autres sont bornées supérieurement; elles vérifient en effet:

T₁ < (C_a.T°₁ + C_b.T°₂ + T°₃)/C_a = T_1max ;
T₂ < (C_a.T°₁ + C_b.T°₂ + T°₃)/C_b = T_2max .

On trouve ici: T_1max = 714 K ; T_2max = 952 K .

Le domaine de définition de la fonction S(T₁, T₂) dans le repère (T₁, T₂) est le triangle défini par les inéquations:

T₁ > 0 ; T₂ > 0 ; T₃ > 0 .

et dont les sommets se situent en (0, 0), (T_1max, 0) et (0, T_2max).
Le diagramme ci-dessous représente le réseau de courbes isentropiques; celles-ci ne peuvent être représentées trop près des frontières, parce que (S) tend alors vers moins l'infini; on a convenu de prendre une température limite T_lim = 100 K .

Le point (I) correspond à l'état initial, (E) à l'état d'équilibre (donc au maximum unique de la fonction (S); ce dernier est situé sur la 1^re bissectrice du repère (T₁ = T₂ = T_f).

[gts2]

(2) dS = (m1C1/T1).dT1 + (m2C2/T2).dT2 + (m3C3/T3).dT3

On ne parle pas de la même équation, donc il y a incompréhension : moi c'est plutôt

"dS = m1C1(1/T1 -1/T3).dT1 + m2C2(1/T2 -1/T3).dT2 = 0 ; relation vraie quelles que soient les valeurs des variations élémentaires (dT1) et (dT2)"
donc vraie en T1=T3 et T2=T3 et donc T1=T2, donc non vraie si T1 et T2 varient.

Quand on intègre l'équation (2), dS=dS(T1,T2,T3), donc la différentielle varie constamment, elle "s'enroule" sur S(T1,T2,T3).
Ici dS=0 est vraie en un point.

[mach3]

(dT₁) et (dT₂) sont les variations élémentaires des températures (T₁, T₂)

C'est dommage, c'est justement le genre de phrase confusante qu'il faudrait éviter. Tout au moins faudrait-il préciser "des variations élémentaires de température non spécifiées". Je suis bien d'accord "qu'entre bandits", on sait de quoi on parle et on se comprend bien, mais dans un lieu de vulgarisation comme ici, il faut tâcher d'éviter ce qui peut être ambigu ou confusant. Comme je l'explique dans un message précédent, penser dS, dT1 et dT2 comme de petites variations, des nombres, peut mener à une compréhension fausse (bon après, il y a pire, comme noter un échange élémentaire de chaleur dQ...). Si on pense en terme de petites variations, mieux vaut les noter avec un petit delta.

m@ch3

[Opabinia]

On ne parle pas de la même équation, donc il y a incompréhension : moi c'est plutôt

"dS = m1C1(1/T1 -1/T3).dT1 + m2C2(1/T2 -1/T3).dT2 = 0 ; relation vraie quelles que soient les valeurs des variations élémentaires (dT1) et (dT2)"
donc vraie en T1=T3 et T2=T3 et donc T1=T2, donc non vraie si T1 et T2 varient.

1°) Tu te réfères à deux égalités:
# dS = m1C1(1/T1 -1/T3).dT1 + m2C2(1/T2 -1/T3).dT2 valable pour tout état, et pour laquelle on a généralement dS ≠ 0 .
# dS = 0 , qui caractérise l'état d'équilibre thermique (point E du diagramme).

2°) La relation dS = m1C1(1/T1 -1/T3).dT1 + m2C2(1/T2 -1/T3).dT2
résulte de la combinaison de deux autres:
# dS = (m1C1/T1).dT1 + (m2C2/T2).dT2 + (m3C3/T3).dT3
# 0 = m1C1.dT1 + m2C2.dT2 + m3C3.dT3
et c'est la seconde expression de (dS) que j'ai préféré intégrer, parce que c'était typographiquement beaucoup plus simple et concis.

J'aurai dû (et sur le papier ce n'est pas du tout insurmontable) partir des dérivées partielles

(dS/dT₁)_T2 = m1C1(1/T1 -1/T3)
(dS/dT₂)_T1 = m2C2(1/T2 -1/T3)

complétées par la relation intégrale

0 = m1C1.(T1 - T°1) + m2C2.(T2 - T°2) + m3C3.(T3 - T°3) ;

Le passage à la primitive 5(T1, T2) s'effectue en deux étapes dont le calcul n'est pas difficile, mais dont le développement conduit à des développements en train de marchandise
La loi du moindre effort et le désir de ne décourager personne m'ont conduit aux calculs du message précédent. Les résultats sont évidemment identiques, et tout aussi bien établis.

Tout cela pour reprendre l'exemple de l'évolution d'un système isolé dont l'état dépend de deux variables, et rechercher l'état d'équilibre qui correspond au maximum de la fonction entropie.

Note: la zone de calcul correspond à une température limite Tlim = 50 K , et non pas de 100 K (la marge grise est alors plus large).

[azizovsky]

Dans le cas d'une fonction d'une variable, on peut définir le "nombre" dérivée en x=x1, valeur de f'(x) en x=x1. On peut écrire l'équation f'(x)=0 pour déterminer x1 correspondant à un extremum.
Dans le cas d'une fonction de n variables, on peut définir les "nombres" dérivées en (x=x1, y=y1 ...). On peut écrire l'équation pour déterminer x1 correspondant à un extremum.
.

1°) Aspect théorique: l'extremum de toute fonction F(x, y, z) dépendant de plusieurs variables indépendantes se caractérise par l'annulation simultanée de toutes ses dérivées partielles, ce qui se traduit ici par les relations:

D_xF = 0 ; D_yF = 0 ; D_zF = 0

.

Soit l'équation du paraboloïde hyperbolique:

pour les , mais la fonction z n'a ni maximum ni minimum en ce point ....(surface en forme de selle)

[Opabinia]

La remarque est pertinente, mais peut recevoir plusieurs réponses.

1°) Le système thermodynamique présente un état d'équilibre et un seul: il existe donc, en l'absence de tout échange avec l'extérieur, un maximum d'entropie, et ce maximum correspond à la solution unique déterminée par le calcul.

2°) La fonction de deux variables S_{(T1, T2)}, définie sur le domaine ouvert de R² délimité par le triangle (OAB), est continue et continument dérivable, et tend vers (-∞) lorsque l'on se rapproche de l'une des 3 frontières, et que la température correspondante (T₁, T₂ ou T₃) tend vers zéro.
Par conséquent la surface d'équation z = S_{(T1, T2)} présente, dans le repère orthonormé (OT₁T₂z), au moins un sommet de cote maximale - c'est l'unique solution repérée, et il n'y a pas d'autres singularités locales (minimum secondaire ou col).

3°) Reprenons les expressions des deux dérivées partielles:

(dS/dT₁)_T2 = m₁C₁(1/T₁ -1/T₃) ;
(dS/dT₂)_T1 = m₂C₂(1/T₂ -1/T₃) ;

elles font intervenir la température (T₃) dont les variations dépendent de celle des deux autres par la relation différentielle:

dT₃ = -C_a.dT₁ - C_b.dT₂ ,

laquelle permet d'exprimer deux autres dérivées partielles:

(dT₃/dT₁)_T2 = - C_a ; (dT₃/dT₂)_T1 = - C_b .

On peut alors passer au calcul des deux dérivées partielles secondes de la fonction entropie:

(d²S/dT₁²)_T2 = m₁C₁.(-1/T₁² + (1/T₃²).(dT₃/dT₁)_T2) = m₁C₁.(-1/T₁² + (1/T₃²).(-C_a)) = - m₁C₁.(1/T₁² + C_a/T₃²) ;

(d²S/dT₂²)_T1 = m₂C₂.(-1/T₂² + (1/T₃²).(dT₃/dT₂)_T1)) = m₂C₂.(-1/T₂² + (1/T₃²).(-C_b)) = - m₂C₂.(1/T₂² + C_b/T₃²) ;

(d²S/dT₁dT₂) = m₁C₁.((1/T₃²).(dT₃/dT₂)_T1) = C_am₃C₃.((1/T₃²).(-C_b)) = - C_aC_bm₃C₃/T₃² .

Noter la symétrie de l'expression de la dérivée seconde mixte.
Les 3 dérivées partielles secondes apparaissent strictement négatives; la concavité de la surface d'équation z = S_{(T1, T2)} se situe donc toujours en-dessous, de sorte que tout point singulier présentant un plan tangent horizontal et vérifiant

(dS/dT₁)_T2 = 0 ; (dS/dT₂)_T1 = 0

correspond nécessairement à un maximum.