Bonjour, j'aurais besoin si possible d'indices:
*Pour la 1ere question je ne sais pas quoi faire
*Pour la 3eme question je ne comprend pas d'où je pourrais faire ressortir le têta
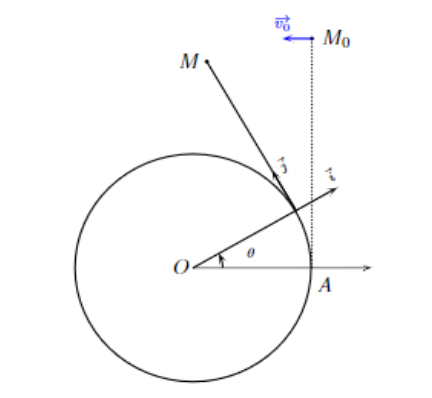
Un point matériel de masse �� se déplace dans le plan horizontal (��, ��⃗⃗,��⃗) et est relié par un fil idéal inextensible de longueur L (inférieure au périmètre du cercle ��) à un point fixe A d'un cercle �� de rayon R.
L'étude est réalisée dans le référentiel ℛ lié au cercle supposé galiléen. On néglige toute force de frottements.
A �� = 0, le point matériel est en ��0 et sa vitesse initiale est ��⃗o.Au cours du déplacement du point matériel, le fil s'enroule sur le cercle ��, et on supposera que le fil reste toujours tendu.
1. Exprimer le vecteur vitesse ��⃗(��)/ℛ du point matériel dans la base (��⃗⃗,��⃗⃗, ��⃗⃗) en fonction de l'angle ��.
2. Déterminer les trois équations qui régissent le mouvement du point matériel.
3. Montrer que ���� −��/2*��22 = ��0*��.
4. Donner l'expression de l'instant ��1 auquel le fil est entièrement enroulé sur le cercle ��.
5. Calculer le module ‖��⃗⃗‖ de la tension du fil à tout instant, le mettre sous la forme
‖��⃗⃗‖ = ��(1 −��/��)1/2
en explicitant les constantes �� et �� en fonction de ��, �� et �� et ��0
L'hypothèse fil tendu est elle justifiée?
-----



 et on dérive.
et on dérive.