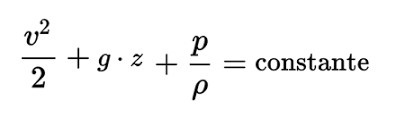Eviter le problème inverse du Queen Elizabeth II

[soliris]

Bonjour,

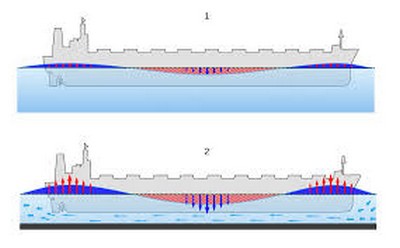
Nous avons déjà parlé de ce qui est arrivé au Queen Eliz. II, en nous portant sur le plan des pressions, et nous avons cité la fameuse constante de Bernoulli.
Nous pouvons bien essayer de dresser la liste des effets (problème inverse) qui sont répertoriés autour des pressions locales et vitesse d'un bateau en milieu aquatique.

Mais pourquoi ne pas tenter une approche en passant pas le débit ?
Ce serait la version "Archimède" de la sustentation d'un volume immergé, mais en mode dynamique..
Donc la question que je pose est plus ou moins la suivante: la quille d'un bateau en mouvement, cad la partie enfoncée dans l'eau, fait bouger une quantité d'eau, par seconde, identique à son débit de remplacement.. non ? Ces mètres-cubes d'eau par seconde fuient dans tous les sens pour laisser passer le bateau.



Donc, pouvez-vous me donner une approche pour faire le lien entre le volume du bateau et sa vitesse d'une part, et son débit de remplacement, d'autre part ? A partir de là, on pourrait, très spécifiquement reprendre le problème du surenfoncement du Queen Elizabeth 2, en parlant cette fois de débit inverse.

Merci d'avance
-----

[FC05]

Renversant !

[soliris]

Renversant ! "La réalité c'est ce qui reste quand on refuse d'y croire" P.K. Dick

"La survenance d'une réalité dépend de notre acceptation." J.L.Soliris

[soliris]

Voilà, finalement, ce n'était pas trop difficile de calculer le "débit de remplacement" d'un volume immergé en mouvement.. Il faut juste connaître ce volume et sa longueur dans le sens du mouvement.

Si par exemple le véhicule a complètement changé d'endroit en 4 secondes (autrement dit: s'il a avancé d'une distance équivalente à sa longueur, en 4 sec), et qu'il fait 20 mètres-cube de volume, alors son débit de remplacement -ou débit inverse- est de 20 m³/4 sec, soit 5 m³/sec.

Donc il ne me reste plus qu'à appliquer cela au Queen Elizabeth ou à tout autre bâtiment, et à m'attaquer, plus particulièrement, au problème du surenfoncement, par le débit sous la quille.

Merci.

Il doit y avoir moyen de faire plus simple, en passant directement par la vitesse du bateau..

[A voir en vidéo sur Futura]

[Opabinia]

Voilà, finalement, ce n'était pas trop difficile de calculer le "débit de remplacement"

Non pas du tout, car la vitesse d'écoulement de l'eau sous le navire dépend aussi du profil de chenal.

En notant (S₁) l'aire de la section droite de la partie immergée du navire dans sa partie la plus large, (S₁) celle du chenal, la vitesse moyenne de l'eau a pour expression (très) approchée

V_e = V_n.S₁/((S₂) - (S₁)) .

La vitesse est d'autant plus grande, et l'effet plus prononcé que le chenal est plus étroit.

[FC05]

C'est encore plus compliqué, vu qu'il y a une vague qui sera poussée devant donc le bateau ne sera pas à plat.

Le fond de la mer n'est pas plat non plus.
La forme de la coque n'est pas simple.
De l'eau passe sur les côtés.

Du coup c'est incalculable par une "formule magique".

[soliris]

la vitesse moyenne de l'eau a pour expression (très) approchée

V_e = V_n.S₁/((S₂) - (S₁)) .

La vitesse est d'autant plus grande, et l'effet plus prononcé que le chenal est plus étroit.

Merci pour cette formule très juste. Mais elle porte l'attention sur les vitesses et non sur le débit. Bien sûr, vous me direz que le débit moyen est Q_(v) = V_e .(S₂-S₁), c'est-à-dire la vitesse moyenne de l'eau tout autour du navire x la section non obstruée du chenal.

Du coup c'est incalculable par une "formule magique".

Ma formule n'est pas bonne parce que si le volume du bateau est démesurément allongé, il est évident que le débit qui remplacera ce volume sera extrêmement retardé; ce qui faussera la donne.
Mais je crois que, puisque la vitesse d'un bateau peut être à un moment considéré comme stable, il existe à coup sûr une formule élégante pour calculer le "débit inverse", sans tenir compte de la forme du véhicule.

C'est vraiment déroutant: si l'on considère tout déplacement, dans le vide spatial ou même quantique, d'un engin, on peut voir besoin d'une théorie de rechange, en forme d'échange.
Par exemple, pour un météore dans l'espace, le fait de calculer son "débit de remplacement local" par le vide, est une chose sur laquelle je médite depuis très longtemps.
Merci de votre participation !

[soliris]

Les formules concernant les débits ne sont pas nombreuses; on a bien sûr Bernoulli et Poiseuille. A propos de Poiseuille, on a quelque chose d'étrange (pour moi): Q(v) = (Pi.r⁴ /L) . (delta p / êta), pour Q(v) = débit, r = rayon, delta P = différentiel de pression entre 2 extrémités considérées, et êta = viscosité.

Le rayon à la 4ième puissance de la formule de Poiseuille est étrange, parce qu'il relève de la 4ième dimension de l'espace et aussi du domaine de l'impulsion volumique qu'on obtient justement en multipliant le volume du bateau par sa vitesse (m⁴/sec).

Comment revenir à un débit en m³/sec, à partir d'une impulsion volumique en m⁴/sec ?

[Opabinia]

Par exemple, pour un météore dans l'espace, le fait de calculer son "débit de remplacement local" par le vide, est une chose sur laquelle je médite depuis très longtemps.

Faire intervenir la mécanique des fluides dans le vide, voilà qui ouvre des perspectives toutes nouvelles ! Comment définiras-tu les lignes de courant suivies par les molécules de vide ? Et comment calculeras-tu la "fameuse constante de Bernoulli" ?

Le rayon à la 4ième puissance de la formule de Poiseuille est étrange, parce qu'il relève de la 4ième dimension de l'espace et aussi du domaine de l'impulsion volumique qu'on obtient justement en multipliant le volume du bateau par sa vitesse (m4/sec)

Et si par accident la différence de pression avait été proportionnelle à (r⁵) ou (r^5/2), dans quelles considérations te serais-tu embarqué ?

[Opabinia]

Remarque très terre-à-terre: une impulsion volumique est une quantité de mouvement rapportée à l'unité de volume, et s'exprime donc en
kg.m.s^-1/(m³) , soit donc en kg.s^-1.m^-2 .

[jacknicklaus]

Le rayon à la 4ième puissance de la formule de Poiseuille est étrange, parce qu'il relève de la 4ième dimension de l'espace

Mon Dieu que c'est beau ! Quel talent !

[FC05]

Mon Dieu que c'est beau ! Quel talent !

C'est bien ce que je disais, renversant !

[soliris]

Remarque très terre-à-terre: une impulsion volumique est une quantité de mouvement rapportée à l'unité de volume, et s'exprime donc en
kg.m.s^-1/(m³) , soit donc en kg.s^-1.m^-2 .

Vous divisez par la quantité de mouvement par le volume.. Moi par la masse volumique "rho".. Ce qui donne au final des "volumes/sec". Certains le font avec les pressions dans Bernoulli:.

[gts2]

"impulsion volumique qu'on obtient justement en multipliant le volume du bateau par sa vitesse"

Cela devient usant, si on appelle une table un poireau, il est évident qu'on va avoir du mal à faire une quiche au poireau.

Une impulsion c'est masse * vitesse
Volumique, c'est du français, on le trouve dans le Larousse : "Se dit d'une grandeur qui est rapportée à l'unité de volume." donc c'est diviser par le volume pas multiplier.

[mh34]

Bon on arrête les dégâts.
Fermeture.