Wikipedia identifie le centre de masse et de poussée, pour les bateaux

[invitef29758b5]

je dis juste que la démo mathématique rigoureuse dans le cas d'un objet partiellement immergé nécessite une hypothèse supplémentaire,

La démonstration utilisant la formule du gradient .
Il suffit d( en prendre une autre
-----

[coussin]

Je pense que c'est un faux problème, si j'ai bien compris...
On peut toujours intégrer sur la surface totale de l'objet, qui est fermée. La partie immergée prendra la pression due à l'eau et la partie émergée prendra la pression due à l'air. Comme la densité d'un gaz est 1000 fois moins qu'un liquide, on neglige la pression atmosphérique, non ?
En tout cas, dans la démo du principe d'Archimède, je n'ai jamais entendu parler de la contribution de l'air agissant sur la partie émergée...

[Black Jack 2]

Bonsoir,

La poussée d'Archimède n'est rien d'autre que la résultante des forces de pressions.

Vérification dans un cas simple:

Soit un parallépipède en bois de base S et de hauteur h de masse volumique Rho(bois)
Il flotte sur l'eau de masse volumique Rho(eau) et la partie émergée est dans l'air de masse volumique rho(air)
Les face du bois de surface S sont horizontales.
L'intensité de la pesanteur est g
La pression atmosphérique est Po au niveau de l'eau.

Soit p la profondeur de la face inférieure du bois.

Le poids du bois est P1 = Rho(bois) * V(bois) * g = Rho(bois) * S * h * g
La pression de l'air au niveau de la face haute du bois est : Po - Rho(air)*g*(d-p)
La force de pression exercée par l'air sur la face supérieure du bois est : (Po - Rho(air)*g*(d-p)) * S (verticale vert le bas)

La pression à la profondeur p est : Po + Rho(eau)*g*p
La force de pression exercée par l'eau sur la face inférieure du bois : (Po + Rho(eau)*g*p) * S (verticale vert le haut)

La résultante des force sur le bois est : R = Rho(bois) * S * h * g + (Po - Rho(air)*g*(d-p)) * S - (Po + Rho(eau)*g*d * S

Et comme le bois flotte, R = 0 -->

Rho(bois) * S * h * g + (Po - Rho(air)*g*(d-p)) * S - (Po + Rho(eau)*g*p) * S = 0

Rho(bois) * S * h * g = (Po + Rho(eau)*g*p) * S - (Po - Rho(air)*g*(d-p)) * S

Rho(bois) * S * h * g = Rho(eau)*g*p * S + Rho(air)*g*(d-p)) * S

Les forces qui équilibrent le poids du bois sont : Rho(eau)*g*p * S + Rho(air)*g*(d-p)) * S

Rho(eau)*g*p * S est le poids du volume d'eau déplacé
Rho(air)*g*(d-p) * S est le poids de l'air pour un volume équivalent à la partie du bois dans l'air.

Donc la "poussée d'Archimède", qui compense le poids d'un objet quand il flotte, est la somme du poids du volume d'eau déplacé ET du poids de l'air correspondant au volume émergé de l'objet.

C'est pareil pour un iceberg ... à ceci près que le calcul est plus compliqué à cause de la forme moins "simple" de l'objet
***********
Pour un bateau.

Pour simplifier le calcul, j'utilise une boîte parallélépipédique ... sans couvercle

Le fond du bateau à une surface S et est à la profondeur p.

En tenant compte que rho(eau) > rho(air), je vais négliger le poids de l'air (on peut faire le calcul complet si on veut)

On a donc Po la pression atmosphérique (considérée ici la même sur toute la partie du bateau qui est émergée)

La force de pression exercée par l'air sur le fond du bateau est : Po * S (verticale vers le bas)

La pression dans l'eau à la profondeur p est : Po + Rho(eau)*g*p

La force de pression exercée par l'eau sur le bateau est donc ( Po + Rho(eau)*g*p) * S (vertical vers le haut)

Le bateau de masse m a un poids m.g (vertical vers le bas)

La résultante des forces sur le bateau est donc : R = m.g + Po * S - ( Po + Rho(eau)*g*p) * S

Et R = 0 puisque le bateau flotte --->

m.g + Po * S - ( Po + Rho(eau)*g*p) * S = 0
m.g = Rho(eau)*g*p * S

(Rho(eau)*g*p * S) est le poids du volume d'eau déplacé.

La force verticale vers le haut qui compense le poids du bateau est donc égale au poids du volume d'eau déplacé... c'est la poussée d'Archimède.

On peut recommencer, si on veut, les calculs en tenant compte que la pression de l'air est un poil différente sur le fond (coté air) du bateau qu'au niveau de l'eau.

On aura alors une composante en plus dans la P Archimède, partie supplémentaire qui correspond au poids du volume d'air dans le bateau entre son fond et le niveau de l'eau ...
ici, elle aura le signe contraire que dans le cas du bloc plein qui flotte ... ce qui est normal puisque dans le cas du bloc plein, la partie émergée prend la place de l'air, alors que dans le cas du bateau, la partie sous eau du bateau permet à l'air de pénétrer dans un endroit où il ne serait pas sans la présence du bateau.

[gts2]

Je pense que c'est un faux problème, si j'ai bien compris.

OK

... la partie émergée prendra la pression due à l'air... dans la démo du principe d'Archimède, je n'ai jamais entendu parler de la contribution de l'air agissant sur la partie émergée...

Si "la partie émergée prendra la pression due à l'air", il faut bien faire intervenir "la contribution de l'air", ou alors je n'ai pas compris la phrase.

Comme la densité d'un gaz est 1000 fois moins qu'un liquide, on néglige la pression atmosphérique, non ?

On néglige plutôt le poids de l'air.

[coussin]

OK


Si "la partie émergée prendra la pression due à l'air", il faut bien faire intervenir "la contribution de l'air", ou alors je n'ai pas compris la phrase.


On néglige plutôt le poids de l'air.

Oui, voilà c'est ça. C'est illustré dans le message ci-dessus de Black Jack 2 : si on veut intégrer sur toute la surface (fermée) de l'objet, la contribution de l'air apparaît. On néglige toujours celle-ci, à ma connaissance, quand on énoncé le principe d'Archimède.

[antek]

On néglige toujours celle-ci, à ma connaissance, quand on énoncé le principe d'Archimède.

On ne néglige pas, elle n'entre pas en jeux dans le principe d'Archimède.

[obi76]

J'ai mal dû me faire comprendre...

Pas grave... bonne fêtes @tous

[gts2]

On ne néglige pas, elle n'entre pas en jeux dans le principe d'Archimède.

Si vous en tenez pas compte, vous tombez sur les problèmes soulevés par obi76.

1- La résultante des forces de pression sur toute la surface fermée fait intervenir le poids de tout le fluide déplacé, et on néglige celui de l'air
2- La résultante des forces de pression de l'eau "uniquement" ne marche pas, il faut faire intervenir la pression de l'air sur la partie émergée.

cf. calcul #33 de @Black Jack 2 ou les miens #28.

Bonnes fêtes à tous.

[coussin]

J'ai mal dû me faire comprendre...

Pas grave... bonne fêtes @tous

Non non, ce que vous avez dit est valide. C'est d'ailleurs passé sous le tapis dans la démo de wikipédia. Je cite

The force exerted on the body can be calculated by integrating the stress tensor over the surface of the body which is in contact with the fluid:

Cette surface, si l'objet n'est pas entièrement immergé, n'est pas fermée. Néanmoins, la ligne d'après fait intervenir une intégration sur une surface fermée et l'application du théorème de Gauss.

https://en.m.wikipedia.org/wiki/Arch...nd_equilibrium

Votre remarque est donc justifiée et il serait intéressant de savoir précisément pourquoi "ça marche quand même".

[Archi3]

le calcul exact pour l'iceberg doit effectivement inclure la poussée d'Archimède de l'atmosphère: on pourrait calculer l'intégrale totale sur sa surface en la décomposant en deux intégrales de surface en coupant l'iceberg au niveau de la surface, avec une pression égale de chaque coté qui s'annule au total :une partie pour l'eau, et une partie pour l'air (2 surface fermées incluant la séparation). en pratique comme l'air est 1000 fois moins lourd que l'eau et qu'en plus il n'y a que un dixième d'émergé, la contribution de l'air est négligeable, de l'ordre de 10^-4 du total, mais en toute rigueur Obi76 a raison - sauf que ça ne contredit pas le principe, il faut l'appliquer aux deux fluides c'est tout.

Avec un objet flottant entre deux fluides de densités différentes mais comparables (par exemple à une interface eau-huile), avec une densité intermédiaire, le calcul exact de la position d'équilibre devrait tenir compte de la poussée d'Archimède des deux fluides.

[Archi3]

bon désolé je n'avais lu que la page 1 je pense que d'autres ont déjà répondu la même chose

[gts2]

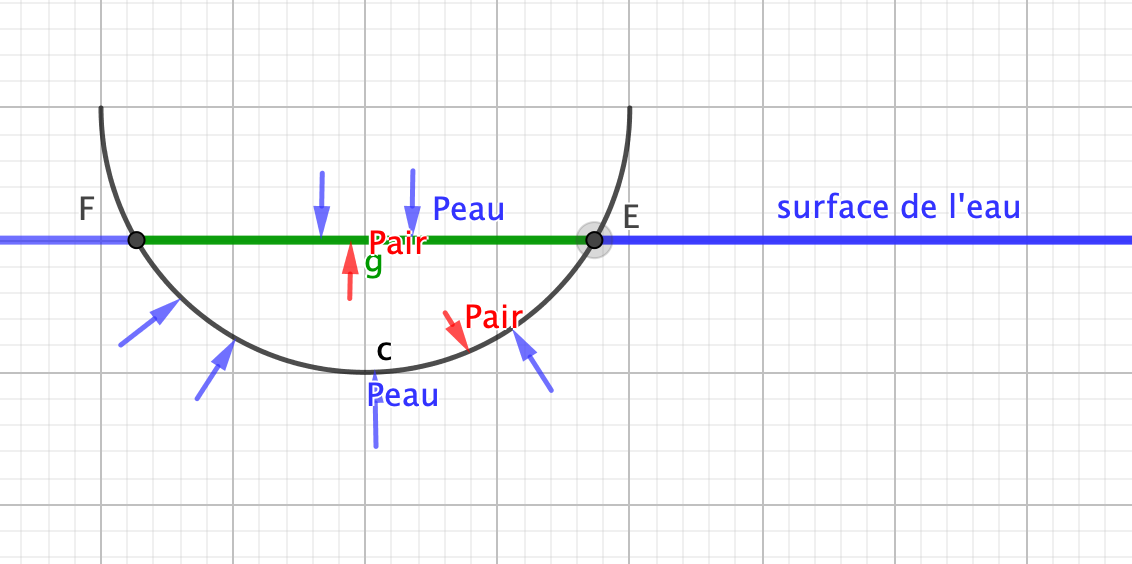
On considère un vaisseau creux dessiné avec des parois minces, mais cela ne joue pas.

On veut calculer la résultante des forces de pression sur la surface fermée qui est constituée par la surface du solide. La pression est celle de l'eau en bleu et celle de l'air en rouge. On ne s'occupe pas de la partie immergée.
L'intégrale peut se découper en deux morceaux sur des surfaces ouvertes correspondant à l'eau et à l'air. on ferme ces deux surfaces par la même surface, le plancher EF.
Intégrale sur l'eau : on peut remplir la surface fermée par de l'eau à l'équilibre, la surface EF est alors à P0, et soit on fait le calcul divergence, gradient ou ... mais aussi plus simplement, on dit que cette eau est à l'équilibre et donc la résultante des forces de pression est l'opposé de son poids.
Intégrale sur l'air : idem sauf que cette fois c'est la force de pression de l'intérieur vers l'extérieur, donc changement de signe : la résultante des forces de pression est égal au poids.
Les deux surface fictives ajoutées se compensent (P0 de chaque côté), donc ne change pas le résultat.

Conclusion : la résultante des forces de pression est l'opposé du poids de l'eau déplacée, auquel il faut ajouter le poids de l'air intérieur (cf. #33 de @Black Jack 2), comme le poids d'air peut être négligé, cela donne bien (heureusement) le résultat attendu.

[coussin]

Ce qui n'est pas forcément justifié est de fermer les deux surfaces par le plancher EF. On pourrait pourquoi pas fermer ces deux surfaces par une autre surface quelconque.
Mon intuition est qu'utiliser le plancher EF est fixé par la direction verticale de la gravité, seule donnée qui fixe une direction non quelconque...

[Archi3]

Ce qui n'est pas forcément justifié est de fermer les deux surfaces par le plancher EF. On pourrait pourquoi pas fermer ces deux surfaces par une autre surface quelconque..

oui on peut prendre n'importe quelle surface de forme quelconque s'appuyant sur le contour délimitant l'interface, dans la mesure où les pressions sont égales et opposées, la contribution à la somme des deux intégrales de pression sera toujours nulle (il est plus logique néanmoins de considérer la surface qui aurait été celle séparant les deux fluides en l'absence du corps).

[gts2]

Ce qui n'est pas forcément justifié est de fermer les deux surfaces par le plancher EF. On pourrait pourquoi pas fermer ces deux surfaces par une autre surface quelconque.

Parce que il faut que les deux termes se compensent, donc même pression P0 des deux côtés et il n'y a qu'une surface qui convienne.
J'ai utilisé le mot plancher pour faire image, mais ce plancher sur le dessin n'est pas quelconque, il est au niveau de la ligne de flottaison.
Il faut aussi que l'eau soit en équilibre ! et là il y a une seule possibilité.

Mon intuition est qu'utiliser le plancher EF est fixé par la direction verticale de la gravité, seule donnée qui fixe une direction non quelconque...

Oui, c'est bien cela, il est horizontal en effet, mais il faut qu'en plus il soit au bon niveau.

[invitef29758b5]

La pression est celle de l'eau en bleu et celle de l'air en rouge.

Si on néglige le gradient de pression de l' air , la pression de l' air , disons 1 bar , se retrouve partout .
Dans l' eau la pression devient (rho.g.h + 1 bar) .
Qu' on prenne en compte cette pression ou pas ne change rien .

[obi76]

Ha je suis content, je me suis donc bien fait comprendre

Oui effectivement, découper en deux et supposer la même pression de part et d'autre de la surface fictive fonctionne, et du coup ça enlève la problématique de la discontinuité

[obi76]

Ce qui n'est pas forcément justifié est de fermer les deux surfaces par le plancher EF. On pourrait pourquoi pas fermer ces deux surfaces par une autre surface quelconque.
Mon intuition est qu'utiliser le plancher EF est fixé par la direction verticale de la gravité, seule donnée qui fixe une direction non quelconque...

Pour préserver la dérivabilité de la pression sur la surface fermée pour pouvoir ensuite utiliser le théorème de flux-divergence, Green-Ostrogradsky, Gauss ou celui que vous voulez

[coussin]

Ha je suis content, je me suis donc bien fait comprendre

Oui effectivement, découper en deux et supposer la même pression de part et d'autre de la surface fictive fonctionne, et du coup ça enlève la problématique de la discontinuité

Si j'ai bien compris, pour un objet partiellement immergé cette surface fictive coupe l'objet en 2. Si l'objet est solide, la pression est effectivement la même de part et d'autre de cette surface fictive par définition d'un solide, non ? Je n'ai jamais entendu parler de contraintes internes à l'intérieur d'un solide...

Ou plutôt : la gravité ne crée pas de gradient de pression dans un solide.

[obi76]

Disons que sur cette surface fictive, quelque soit la pression que l'on met, la résultante s'annule (puisqu'on coupe l'objet initial en 2objets ayant cette surface en commun). Du coup il ne reste "que" à choisir la pression ad-hoc pour que la démo mathématique soit bonne (i.e. dérivable dans l'espace), pour obtenir deux objets fermés où le gradient / la divergence sont déterminés en tout point du volume.

[gts2]

Si j'ai bien compris, pour un objet partiellement immergé cette surface fictive coupe l'objet en 2. Si l'objet est solide, la pression est effectivement la même de part et d'autre de cette surface fictive par définition d'un solide, non ? Je n'ai jamais entendu parler de contraintes internes à l'intérieur d'un solide.

Pour un solide plein, il n'y a aucun problème, il plonge dans un fluide constitué pour partie d'eau, pour partie d'air, donc la poussée d'Archimède est l'opposée du poids d'eau et d'air déplacé, et on peut négliger le poids de 'air.

Le problème se pose pour un solide creux, car alors le remplacement du solide par le fluide "déplacé" conduit à un système hors équilibre, en-dehors d'Archimède strict, mais on peut s'y ramener.

[obi76]

Je reviens à ma ventouse : pour fermer la surface, il faut prendre le fond de la baignoire, sur laquelle la pression exercée n'est pas celle de l'eau mais celle de l'air à l'intérieur de la ventouse.

[coussin]

La ventouse est cité comme un cas où le principe d'Archimède ne s'applique pas...

[obi76]

Tout se tient, donc

[coussin]

Qui eut cru qu'un sujet de Soliris puisse devenir si intéressant

[Sethy]

Qui eut cru qu'un sujet de Soliris puisse devenir si intéressant

https://youtu.be/ziKDiDRO4jw?t=54