Exercice plan incliné

[Ayako07]

Bonsoir! Je bloque sur un exercice assez trivial de physique et j'ai du mal à identifier le problème. Voilà l'énoncé :

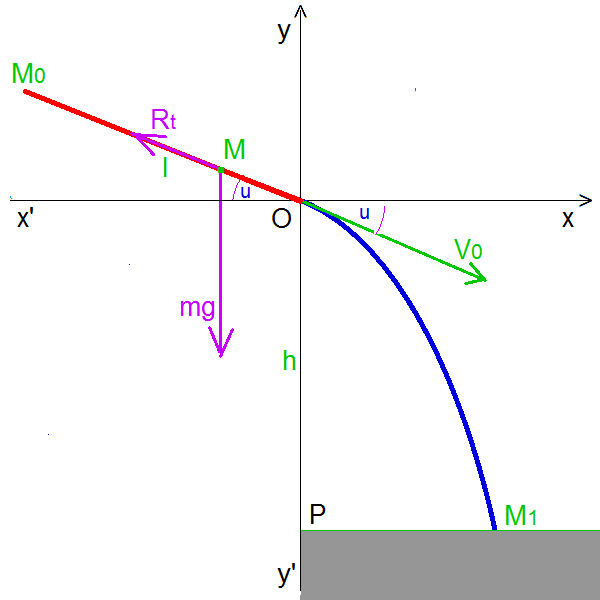
Un corps glisse du haut du toit d'une maison sans vitesse initiale. Lorsque le corps quitte le toit, il se trouve à une hauteur de 10 m du sol. Le toit fait un angle de 35◦ par rapport à l'horizontale. La longueur de la pente est de 5 m et le coefficient de frottement est de 0,3. A quelle distance de la maison le corps va-t-il toucher le sol?

Voilà mon raisonnement :

Px = P*sin(a) et N = P*cos(a)
m*a = Px - Ff et Ff = µc*N
La masse de l'objet n'étant pas précisée, je pars du principe que m = 1kg (donc P = 10N) pour simplifier les calculs. Donc,

1*a = 10*sin35 - 0,3*10*cos35
a = 3,278 m/s²

x(t) = x0 + v0*t + 0,5*a*t²
5 = 0,5*3,278*t², donc t = 1,746
a = v*t, donc v = a / t = 2,3278 / 1,746 = 1,33 m/s (vitesse atteinte par le mobile au bout de la pente)

10 = 0,5*10*t², donc t = 2^0,5 (temps que mettra le mobile à atteindre le sol)
x(t) = v*t = 1,33*2^0,5 = 1,88 mètres

Est-ce que quelqu'un sait m'aider à identifier mes erreurs ? Merci d'avance!
-----

[gts2]

Déjà la masse est inutile, puisqu'elle se simplifie dans tous les calculs.

Pour le parcours sur le toit, un raisonnement énergétique aurait été plus rapide, mais je ne vois pas de pb.

Par contre, pour la chute libre, les conditions initiales ne sont pas les bonnes, à moins qu'il y ait un tremplin : la vitesse de 1,33 m/s n'est pas horizontale.

[Opabinia]

Bonjour,

Il n'y a aucune raison d'attribuer à la masse la valeur unité; cette donnée doit disparaître spontanément des calculs.

Un corps glisse du haut du toit d'une maison sans vitesse initiale. Lorsque le corps quitte le toit, il se trouve à une hauteur de 10 m du sol. Le toit fait un angle de 35° par rapport à l'horizontale. La longueur de la pente est de 5 m et le coefficient de frottement est de 0,3. A quelle distance de la maison le corps va-t-il toucher le sol?

Le mouvement comporte deux phases.

1°) Le glissement avec frottement sur le toit: il faut connaître la norme de la vitesse (V₀), et il suffit de considérer que l'énergie cinétique acquise par le mobile sur le trajet correspondant (M₀O) est égale au travail des forces agissantes:

E_c(O) - E_c(M0) = (1/2)mV₀² - 0 = W_(mg) + w_(Rt) = mgl.Sin(u) - fmgl.Cos(u) ;

il vient dans ces conditions:

V₀² = 2gl(Sin(u) - f.Cos(u))

et numériquement:

V₀ = (2*9.81*5(Sin(35) - 0.3*Cos(35)))^1/2 = 5.6710 ~ 5.7 m/s .

2°) La chute libre à partir du bord du toit, que l'on prend pour origine du repère, et dont la date correspond à l'origine des temps: simple problème de cinématique dépourvu de difficultés, avec les conventions prises.

[Opabinia]

Bien sûr, ne pas faire d'approximation numérique en cours de calcul, et prendre pour la suite V₀ =5.6710 m/s .

[A voir en vidéo sur Futura]

[gts2]

Sinon v=a*t et pas l'inverse.

[Ayako07]

Merci pour vos réponses!

Sinon v=a*t et pas l'inverse.

Effectivement, merci!

Bien sûr, ne pas faire d'approximation numérique en cours de calcul, et prendre pour la suite V0 =5.6710 m/s .

J'ai refait le calcul sans attribuer de valeur arbitraire à m et, évidemment, j'ai obtenu le même résultat. (a = 3,278 m/s²) Si le résultat final est le même, dans quelle mesure est-ce un problème?

Sinon, à partir du moment où le mobile quitte le plan incliné, je ne sais pas comment procéder... J'ai essayé de calculer la vitesse horizontale en faisant v0*cos(35) = 4,69 m/s, puis x(2^0,5) = 4,69*2^,05 = 6,63, et le correctif m'indique que la réponse n'est pas la bonne...

Autrement, je profite de ce sujet pour éviter d'avoir à polluer le forum avec mes questions triviales, voilà deux autres énoncés qui me posent problème :

Un disque de diamètre 1 m est animé d'un mouvement de rotation autour de son axe, d'accélération angulaire 5 rad/s2, de l'arrêt jusqu'à 20 tours/minute. Combien de tours a-t-il effectué pendant ce temps? Quelle est la distance totale parcourue par un point à la périphérie du disque?

Je sais que R = 0,5, que a = 5, que w0 = 0, que wf = 20 et je dois chercher t = ? et x = ?.
Je sais que le périmètre du cercle = 2*pi*0,5 = pi.
wf = w0 - a*t
t = wf / a = 20 / 5 = 4 sec

θ = θ0 + w0*t + 0,5*a*t²
θ = 0 + 0*4 + 0,5*5*16 = 40 rad (et là, je me rends compte qu'il y a un gros problème :/)

La vitesse angulaire maximale atteinte par le module est de 20 tours/minute et j'obtiens qu'en 4 secondes d'accélération à 5 rad/s², le module a fait un angle de 40 rad. :/ Où est-ce que je me suis trompée ?

Dernier énoncé sur lequel je bloque :

Une roue cylindrique tourne avec une accélération angulaire constante de 4,0 rad/s2. Lorsqu'elle atteint la vitesse angulaire de 2,0 rad/s, un point de sa périphérie a une accélération totale de 8 m/s2. Quel est le rayon de la roue?

Ici, je bloque totalement... Je pense que c'est le terme "accélération totale" qui me pose problème, j'ai essayé de faire les calculs avec l'accélération angulaire et l'accélération radiale et le résultat était systématiquement mauvais. Comment obtenir cette accélération ? Et comment l'utiliser pour résoudre le calcul ? (je ne connais aucune formule en MCU qui l'utilise)

Voilà, j'espère que je ne dérange pas en posant toutes ces questions! Dernière petite chose, si j'ai d'autres questions sur d'autres chapitres en physique sur lesquels je suis en train de travailler, est-ce que je peux reposter sur ce sujet pour éviter de polluer le forum, ou dois-je créer un nouveau sujet avec le titre adéquat ?

Merci d'avance!

[gts2]

"4,69*2^,05 = 6,63" voulez-vous dire ? D'où sort ce sqrt(2) ? ou alors ?
C'est une trajectoire parabolique avec accélération verticale g et vitesse initiale connue.

Pour le 2, l'accélération angulaire est donnée en rad/s2 et la vitesse angulaire en tour/minute !

Pour le 3, "un point de sa périphérie a une accélération totale", je suppose que cela veut dire l'accélération tout court ?
Il faut écrire et dériver deux fois. Vous devriez voir apparaitre votre accélération angulaire et le carré de la vitesse angulaire.

[Ayako07]

"4,69*2^,05 = 6,63" voulez-vous dire ? D'où sort ce sqrt(2) ? ou alors ?
C'est une trajectoire parabolique avec accélération verticale g et vitesse initiale connue.

10 = 0,5*10*t², donc t = 2^0,5
C'est le temps que mettra le mobile pour atteindre le sol selon son accélération verticale, je me trompe ?
Donc je multiplie 4,69 m/s par le temps que mettra le mobile pour toucher le sol afin d'obtenir la portée horizontale du mouvement.

Pour le 2, l'accélération angulaire est donnée en rad/s2 et la vitesse angulaire en tour/minute !

Effectivement, merci! Donc 20/60 = 0,333 Hz
wf = 2pi * 0,333 = 2,094

t = wf / a = 2,094 / 5 = 0,419 sec
θ = 0,5*5*0,419² = 0,4389 rad
θ = x / R, donc x = θ * R = 0,4389 / 2 = 0,219 m
et 0,4389/2pi = 0,069 tour

Je ne me suis pas plantée dans mon raisonnement ?

Pour le 3, "un point de sa périphérie a une accélération totale", je suppose que cela veut dire l'accélération tout court ?

Ça ne correspond pas à l'accélération angulaire, ni à l'accélération tangentielle, ni à l'accélération radiale...

Il faut écrire et dériver deux fois. Vous devriez voir apparaitre votre accélération angulaire et le carré de la vitesse angulaire.

Je ne vous suis plus... Pourquoi dériver deux fois ?
On me donne l'accélération angulaire et la vitesse éponyme dans l'énoncé.

[gts2]

"10 = 0,5*10*t²" ; et la vitesse initiale à t=0 ?

Pour le 2, cela parait OK

"Ça ne correspond pas à l'accélération angulaire, ni à l'accélération tangentielle, ni à l'accélération radiale..."
Non cela correspond à l'accélération du point à la périphérie disons M.

"On me donne l'accélération angulaire et la vitesse éponyme dans l'énoncé."

Oui mais on veut l'accélération du point M, il faut calculer son accélération pour établir le lien avec les données.