Bonjour,
Je suis face à un problème de quantité de mouvement, j'ai eu cet exercice deux fois déjà à un examen et je n'ai pas réussi à le résoudre, les deux fois, je peux essayer de refaire et vous montrer ce que j'avais fait, mais je doute qu'en ayant eu respectivement 2 et 4/20 je sois proche de la solution...
Je cherche donc quelqu'un qui pourrait m'aider à obtenir le bon résultat
Bien cordialement,
Mathieu
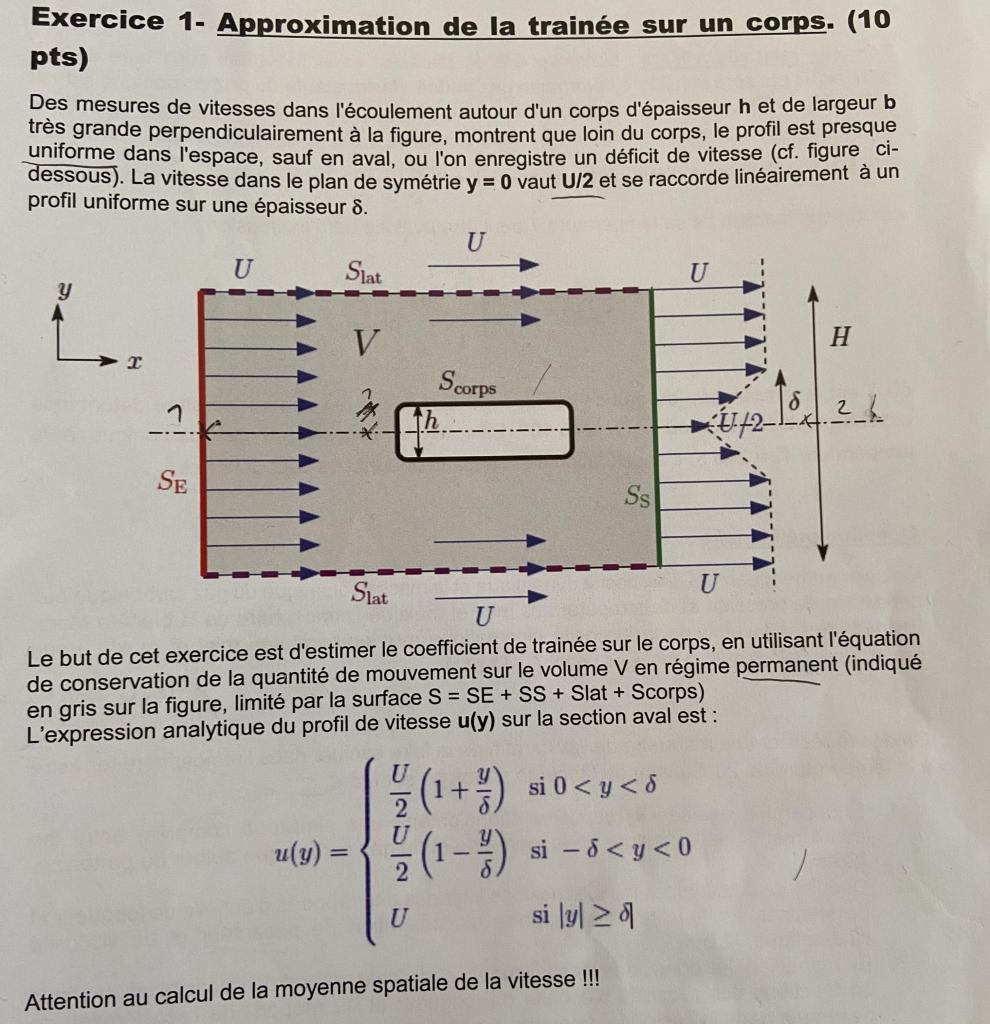
-----



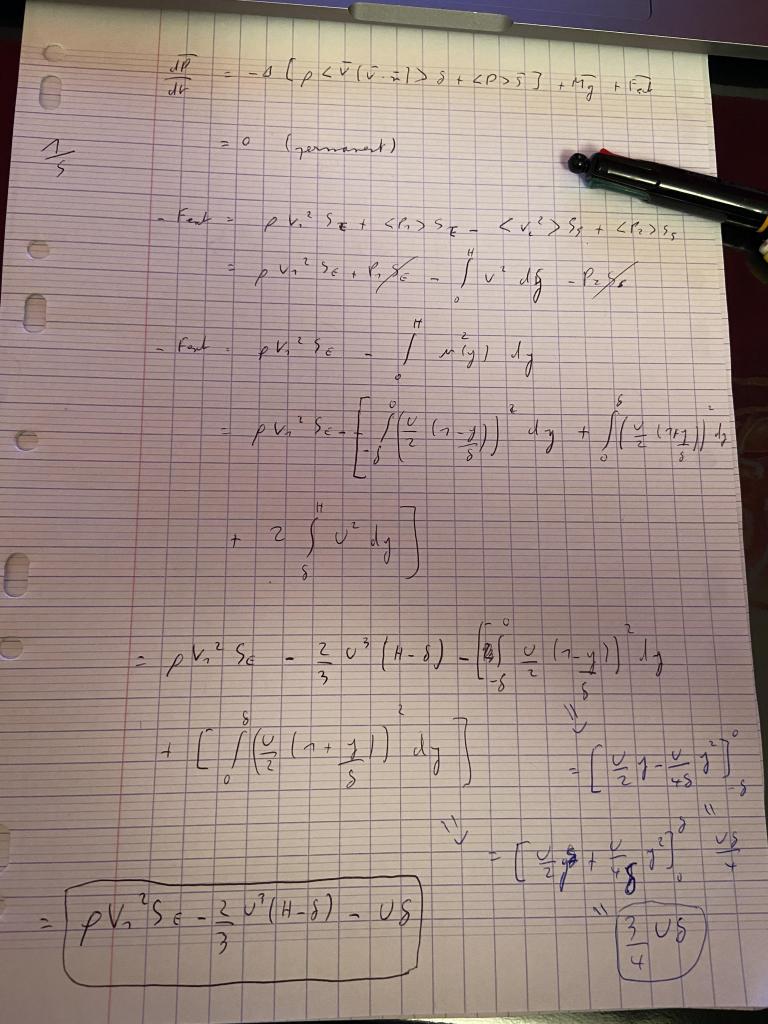
 à
à 


