Mécanique des solides 2D

[Phoboe]

Bonjour,

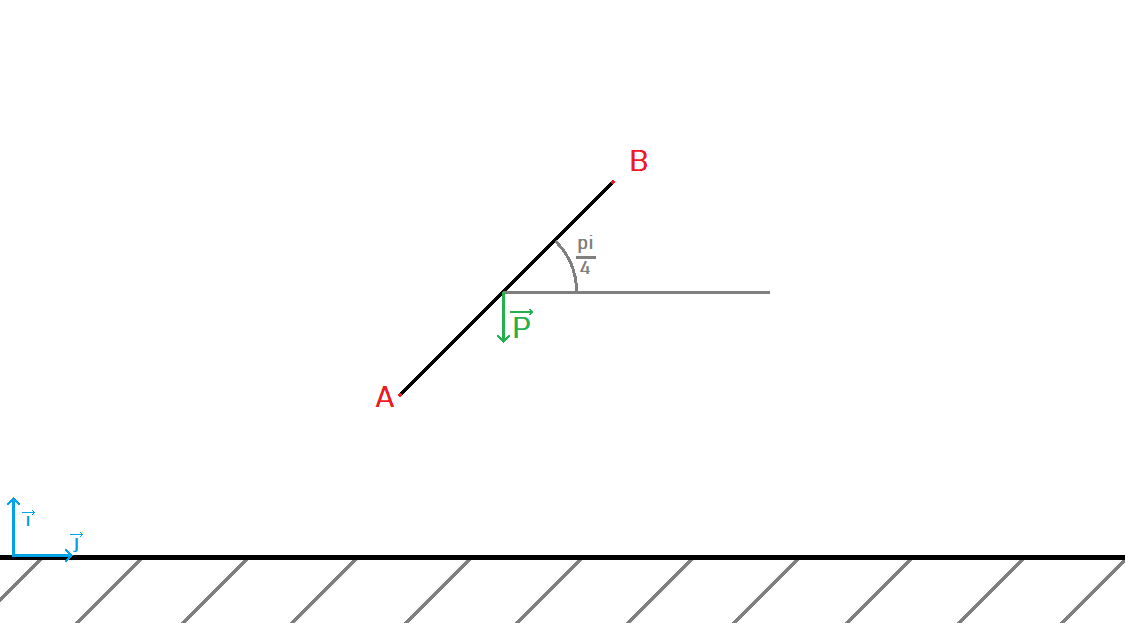
J'essaye en ce moment de programmer une petite simulation et je souhaiterai pouvoir prendre en compte le système suivant :



Je précise que l'objet est un segment possédant une masse linéique et n'est donc pas assimilable à 2 points rigidement liés. La masse de l'objet est arbitraire et toutes ses vitesses son nulles initialement.

La seule force que subit l'objet est son poids, ayant une masse de 1. (Kg)

Pourriez-vous m'aiguiller sur les outils mathématiques (vecteurs, matrices..) dont j'ai besoin pour résoudre ce genre de problème, ainsi que les équations qui sont nécessaires ?

Merci à tous !

Autres données :
longueur : 50 cm
épaisseur : tendant vers 0 (ou nulle)
coefficient de rebond : e = 0.3
-----

[SoloMan67]

Quand tu dis que les points A et B ne sont pas assimilable à 2 points «*rigidement liés*», tu aimerais enfaite que ton segment se comporte comme une corde qu’on laisserait tomber du haut d’une tour par exemple ?

[Phoboe]

Bonjour SoloMan67,

Je veux dire que le segment n'est pas considéré comme deux points matériels contraints par une distance irréductible, (mécanique du point) mais qu'il est comme un bâton disons, c'est un objet ayant une masse linéique propre avec deux extrémités.

Est ce que j'ai réussi à clarifier mon problème ?

[SoloMan67]

D'accord donc le segment se comporte bien comme un segment rigide, j'avais mal compris

Donc pour simuler ce système, tu dois dois simuler l'action du Poids sur le point A et B, et l'interaction du point A sur le point B et inversement à travers le segment. Le mieux serai de dire que la moitié du poids se trouve sur le point A, et l'autre moitié sur le point B

[A voir en vidéo sur Futura]

[Dynamix]

Le mieux serai de dire que la moitié du poids se trouve sur le point A, et l'autre moitié sur le point B

Ce qui fausserait le moment d' inertie .

[SoloMan67]

C’est vrai, mais pour la simulation ça marcherait bien

[Phoboe]

Bonsoir, j'ai essayé cela mais le résultat n'est pas naturel.. Seulement je n'arrive pas à trouver les equations assez poussées qui me permettent de faire mieux.

Si on assimile l'objet à un rectangle de largeur tendans vers 0 vous pensez qu'on peut s'amuser ?

[jacknicklaus]

C’est vrai, mais pour la simulation ça marcherait bien

c'est vrai, mais alors ca simulerait un autre problème que celui posé.

[SoloMan67]

Bonsoir, j'ai essayé cela mais le résultat n'est pas naturel.. Seulement je n'arrive pas à trouver les equations assez poussées qui me permettent de faire mieux.

Si on assimile l'objet à un rectangle de largeur tendans vers 0 vous pensez qu'on peut s'amuser ?

Tu as simulé le système avec quels forces ? Et en quel language ?

[Phoboe]

C'est exact.

Le mouvement du pendule fait référence à ce genre de simulations
Lors qu'on ne considère qu'aucun point est fixe, mais qu'on considère les 2 points libres et qu'on utilise les équations que l'on utilise en L1 pour le pendule, c'est chelou haha
Le résultat est bizarre parce que physiquement on ne peux pas assimiler ce système pourtant assez simple à un couple de points

Croyez moi j'ai tourné le problème dans tous les sens !
je ne vois que cette issue

[SoloMan67]

c'est vrai, mais alors ca simulerait un autre problème que celui posé.

Je me trompe peut être mais je pense pas que ça simulerait un autre problème que celui posé. Si on programme ce système avec la moitié du poids au point A, l’autre moitié au poids B, et en définissant le lien entre A et B comme étant rigide on aurait un résultat similaire à un segment avec une densité linéique constante

[Phoboe]

Tu as simulé le système avec quels forces ? Et en quel language ?

J'ai considéré uniquement les forces de répulsion du sol et le poids.
Je néglige les frictions avec le sol et les frottements de l'air pour le moment

* et j'utilise python

[SoloMan67]

Comment tu as définis la force de répulsion ? Avec quelle expression ?
Comme tu me le décrit ça devrai donner un truc à peu près réaliste si on néglige le frottement, et qu’on considère la distance entre A et B comme constante et que chaque point contenu entre A et B ne peuvent pas avoir une altitude inférieur à 0

[Phoboe]

La force de répulsion lors de la collision avec le sol est égale à -P, P étant le poids.
C'est ce que j'utilise, je ne sais pas si c'est juste
et ce sera égal à -P.e avec e le coefficient de rebond élastique si on le considère différent de 1.

[Phoboe]

Je l'applique en prenant en compte l'écartement du point d'application de cette force avec le centre de gravité de l'objet (V = r.omega)
Et je répartit la distribution "vitesse linéaire" et "vitesse angulaire" selon la composante tangentielle et normale de cette force de répulsion du sol

C'est correct ?

[jacknicklaus]

Je me trompe peut être

En effet. moment d'inertie d'une barre homogène de masse M, longueur L, par rapport au centre : ML²/12
moment d'inertie de 2 points matériels chacun de masse M/2, réunis par une tige de masse nulle de longueur L, par rapport au centre : ML²/4

Y'a juste un rapport 3 entre les deux, excusez du peu de différence...