Filtres passe-haut et passe-bas en cascade : fréquences de coupure

[Realgur]

Bonjour à tous,

je souhaiterais vous soumettre une question sur laquelle je me gratte la tête depuis un bon moment.

Je travaille sur un projet d'éléctronique avec un ami, et nous souhaitons intégrer un filtre passe-haut et un filtre passe-bas en cascade dans notre circuit.
Le principe est d'utiliser des potentiomètres (R1 et R2) pour ces deux filtres afin de pouvoir faire varier les fréquences de coupure. Les condensateurs utilisés seront de même valeur C
Le montage est donc une cellule RC et une cellule CR séparées par un montage suiveur (AOP ou transistor) de manière à ce que les impédances soient séparées et que les deux filtres ne "s'influencent" pas. Le suiveur permet d'établir que la fonction de transfert totale est le produit des fonctions de transfert respectives des deux filtres tel que : H = H1*H2
Ainsi H1 aura une fréquence de coupure de f₁= et H2 aura une fréquence de coupure de f₂=
Le diagramme de Bode de la fonction de transfert H sera la somme "graphique" des deux diagrammes de Bode de H1 et H2. Il semble donc logique que les deux fréquences de coupure seront indépendantes et donc que modifier la valeur de l'une (à l'aide d'un pot') n'aura pas d'incidence sur celle de l'autre.

Mais je suis tombé sur quelque chose qui me semble incohérent en approfondissant mes calculs.
En effet j'ai voulu calculer la valeur des pulsations de coupure à partir de la fonction de transfert totale H pour voir si je retombais bien sur celles énoncées plus haut.
On a
Ainsi on a

On peut donc identifier cette fonction de transfert à la forme canonique de la fonction de transfert d'un passe-bande d'ordre 2 pour identifier le gain statique , le facteur de qualité Q ainsi que la pulsation propre .
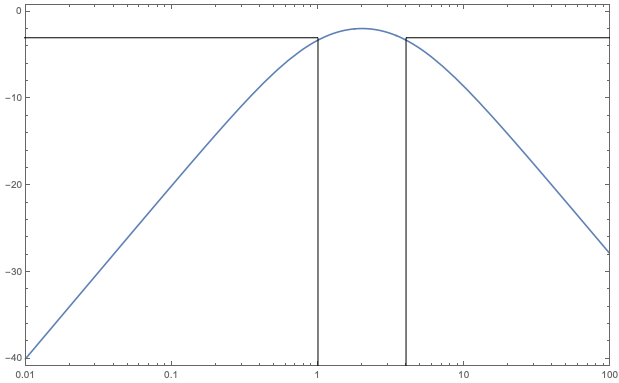
Mais on sait que les pulsations de coupure sont caractérisées par une perte de 3 dB par rapport au gain max soit que G(w1)=G(w2)=Gmax/sqrt(2)
On peut donc résoudre cette équation pour exprimer les pulsations de coupure en fonction des caractéristiques du circuit, telles que :


Vous l'aurez deviné, en remplaçant par les grandeurs du circuit, je ne trouve pas du tout 1/R1*C et 1/R2*C, et encore pire, je trouve des pulsations (et donc des fréquences) de coupure qui dépendent des deux résistances ce qui voudrait donc dire que les deux fréquences de coupure ne peuvent être modifiées indépendamment l'une de l'autre.

Je ne comprends pas ou est l'erreur de raisonnement et ne sait pas à quel résultat me fier, et je serais extremement reconnaissant d'avoir vos avis et éclaircissements sur la question!
Merci à tous d'avance.

Désolé de la longueur du post et bonne soirée!
-----

[Antoane]

Bonsoir et bienvenue sur Futura,

Pour que les deux fréquences de coupures soient absolument indépendantes et valent f_i=1/(2πR_iC), il faudrait que le gain du filtre j à la fréquence f_i soit égal à 1, ce qui n'est pas nécessairement le cas
Cas particulier : que se passe-t-il avec ton raisonnement si R1 = R2 ? Ou si la fréquence de coupure du passe-haut est supérieure à celle du passe-bas ?

Tu peux essayer de simplifier les expressions de w_i lorsque R1 << R2.

[Realgur]

Merci de ta réponse rapide,
R1 serait en 4k et 100k et R2 entre 1 et 1k. J'ai choisi ces valeurs en considérant la fréquence de coupure 1/2πRC pour avoir des coupures jusqu'à 1600 Hz pour le passe haut et jusqu'à 400Hz pour le basse bas. Donc il n'y jamais d'égalité, mais si ces expressions sont fausses pour les fréquences de coupure, les valeurs de résistance n'ont pas lieu d'être.
Je ne saisis pas pourquoi le raisonnement sur le deux fréquences de coupures de FT d'ordre 1 ne fonctionne pas. Je suis un peu perdu!

EDIT : pour R1=R2 j'obtiens Q=H0=1/2, donc j'obtiens un gain max bien inférieur à 1, et donc je ne peux pas traiter les deux frequences de coupure indépendamment selon ce que tu m'as dit

[gts2]

Bonjour,

Avec 1 décade entre les deux fréquences de coupure, cela marche.

EDIT : un facteur 4 c'est en effet un peu limite.

[A voir en vidéo sur Futura]

[gts2]

"1600 Hz pour le passe haut et jusqu'à 400Hz pour le basse bas"

L'inverse non ?

Sinon l'approximation n'est pas si mauvaise (ligne verticale fréquence de coupure, horizontale -3dB) :

[Realgur]

Le facteur 4 c'est vraiment le strict minimum, mais dans la plupart des cas ça sera beaucoup plus. Donc cela veut dire que l'indépendance des fréquences de cutoff dépend du rapport R1/R2? D'où cela vient-il?
J'ai modélisé sur MatLab mes fonctions de transfert et a priori je peux faire bouger l'un des fréquence sans influencer l'autre (je n'ai pas essayé pour des valeurs extrêmes) mais je pense que dans le cas général cela fonctionne.
Je n'arrive juste pas à conceptualiser ce qui définit si les deux fréquences sont liées et qu'elle formule pour les cutoff est la bonne.

En tout cas vos éléments de réponses me font avancer c'est déjà super!

[Realgur]

Oui évidemment c'est l'inverse excuse moi je confonds toujours!
J'attends la validation pour consulter ta pièce jointe.

[gts2]

Si vous raisonnez en diagramme asymptotique, il n'y a pas de problème, mais justement il ne faut pas oublier que c'est un diagramme asymptotique.

Dessinez à la main vos deux diagrammes asymptotiques puis réels en insistant lourdement sur l'écart courbe-asymptote. Additionnez vos deux diagrammes réels et concluez comme @Antoane dans le message #2
"il faudrait que le gain du filtre j à la fréquence fi soit égal à 1"
ou dit visuellement, il faut atteindre l'asymptote du premier filtre avant que le second n'agisse.

[Realgur]

D'accord, je crois avoir compris d'où venait le problème. Merci beaucoup !
Je me demande juste d'où vient la différence "mathématique" entre les deux expressions, car les deux se basent sur le diagramme réel non?

En tout cas merci beaucoup, je peux confirmer que mon montage fonctionnera comme escompté dans la plupart des cas.

[gts2]

Je me demande juste d'où vient la différence "mathématique" entre les deux expressions, car les deux se basent sur le diagramme réel non ?

Question à préciser : de quelles expressions parlez-vous ? de quelle différence parlez-vous ?

Sinon, votre fonction de transfert était factorisée, je ne vois pas l'intérêt de la "défactoriser", on cherche :
On voit bien qu'on obtiendra correspondant à l'une des fractions que si l'autre fraction est égale à 1 (cf. message initial de @Antoane)

[Realgur]

Je n'ai pas été très clair effectivement.
Je vais reformuler: tout l'objet de mon problème est de comprendre pourquoi en utilisant la forme factorisée de la fonction de transfert j'obtiens , donc que faire varier un des potentiomètres ne modifiera qu'une seule des fréquences de coupures, sans influer sur l'autre (c'est le fonctionnement que je recherche); alors qu'en utilisant la forme développée de H, j'arrive à deux expressions différentes, dépendant de R1 ET de R2, ce qui voudrait dire que modifier un potentiomètre changera les deux fréquences de coupure (ce n'est donc pas le fonctionnement que je recherche).
Pourquoi trouvons nous deux expressions non équivalentes et d'où vient l'erreur de raisonnement? Laquelle est juste?
Merci!

[gts2]

La fréquence de coupure d'un premier ordre est la cassure de la courbe asymptotique et si vous mettez deux premier ordre en cascade, les deux cassures ne vont pas changer, mais les courbes réelles si.

Autrement dit la cassure de la courbe asymptotique ne donne -3dB que si le filtre est seul.

[Realgur]

Cela veut donc dire que définir les pulsations de coupure par l'équation :
n'est pas valable pour deux filtres en cascade? Et donc que c'est bel et bien l'expression l'expression valable?

[gts2]

En fait, il y a deux notions : celle de pôles et donc fréquences caractéristiques et celle de fréquence de coupure à -3dB.
Dans le cas d'un premier ordre seul, les deux notions donnent la même chose.
Lorsqu'on fait une mise en cascade, les pôles se conservent mais pas les fréquences de coupure.
Mettez en cascade deux passe-bas de premier ordre de même fréquence caractéristique donc fréquence de coupure, vous obtenez un passe-bas d'ordre 2 de même fréquences caractéristiques (les pôles n'ont pas changés), par contre pour cette fréquence, le gain est de -6dB.

[Realgur]

Que vous voulez vous dire par "fréquences caractéristiques"? C'est ?
Donc pour le cas d'un ordre 2, les fréquence de coupure à -3dB ne sont plus égales aux fréquences de coupures à -3dB (qui sont sont égales à 1/2πRC si j'ai bien compris) des deux ordres 1, qui correspondent alors a des fréquences de coupure à -6dB?

[Realgur]

Et je n'ai également pas compris quand vous avez dit "avec 1 décade entre les deux fréquences de coupure cela marche". Comment cela se fait-il?

[gts2]

J'appelle fréquence caractéristique la grandeur la plus simple pour caractériser un filtre.
Pour un premier ordre , la pulsation caractéristique est , c'est aussi la fréquence de coupure à -3dB, l'opposé du pôle, l'intersection des asymptotes dans un diagramme de Bode.
Pour un deuxième ordre non factorisable , la pulsation caractéristique est , ce n'est pas la fréquence de coupure à -3dB, ce n'est pas l'opposé de la partie réelle du pôle, mais c'est bien l'intersection des asymptotes dans un diagramme de Bode (il y a manifestement un deuxième paramètre m).

Pour l'éloignement d'une décade,
1- on s'intéresse à la norme donc on fait apparaitre , donc avec un facteur 10, on a soit , soit , l'écart par rapport à l'asymptote (10 ou 1) est de 0,5%.
2- on est en dB et un écart de 0,5% donne 0,04 dB donc tout à fait négligeable.

Pour le produit de deux ordre 1 identiques, en effet, le pôle se conserve, la fréquence caractéristique se conserve, la rencontre des asymptotes aussi, mais pas la fréquence de coupure à -3dB.

[Realgur]

Ma fonction de transfert est du type je ne sais pas si cela change quelque chose.
Donc en conclusion les deux formules sont équivalentes pour mon filtre tant que les deux asymptotes sont suffisamment écartées ? Et si ce n'est pas le cas par laquelle dois-je passer? (Cf mon premier post sur mon problème de qu'elle formule utiliser)
Merci!

[gts2]

Si vous voulez parler des deux formules donnant les fréquences de coupure à -3dB, la deuxième formule est générale (avec Q), alors que la première (avec 2 pi RC) n'est qu'approximative.

"les deux formules sont équivalentes pour mon filtre tant que les deux asymptotes sont suffisamment écartées ? "

Tant que les deux fréquences de coupure sont suffisamment écartées, mais le suffisamment n'est pas très méchant : même avec votre facteur 4 (400*4=1600) on trouve pour 400 Hz un gain du passe-bande de -3,3 dB.

[Realgur]

C'est tout ce que je voulais savoir!
Grand merci a vous d'avoir pris du temps pour m'expliquer!
Bonne continuation