Bonjour tout le monde, je suis bloqué sur un exercice de moment d'inertie, j'imagine qu'il faut utiliser le théorème de Huygens/Steiner mais je ne comprends pas vraiment comment il s'utilise. Grace aux formulaires donnant le moment d'inertie par apport à chaque axe pour différents solides j'ai pu faire le calcul des 3 corps pour le moment d'inertie par apport au centre de masse mais une fois que je dois le calculer via un autre point je bloque ? Merci d'avance
Bonjour,
Le calcul m'a l'air correct. Où est le problème ?
Bonjour, justement je ne parviens pas à comprendre pourquoi le x4 , le x1,25 etc ? J'ai essayé de vérifier avec la formule de Huygens qui dit que le moment d'inertie par apport à un point P est la distance au carré par apport au centre de masse + la masse mais ca reste incorrect pour le 1,25 ?? A la rigueur pour le X4 on peut prédire que c'est parce que le centre de masse de la cabine et du moteur se situe à 2M du point P et 2 au carré donne 4 mais le 1,25 ?
Merci. !!
Le 1,25 c'est la même chose : le centre d'inertie du rectangle est à 0,5m de P selon I3 et 1m selon I1. Donc d2=0,52+12=1,25 m2
Super merci infiniment donc si je comprends bien toujours prendre la distance selon chaque composante et l'élever au carré et faire la somme de toutes les composantes de la distance le tout multiplié par la masse? .. J'ai encore deux questions: pour cet exercice-ci (cf image) je ne comprends pas pourquoi est ce que l'on choisi le moment d'inertie principale selon i2/i1 (c'est le meme) pour le cylindre 2 et seulement le moment d'inertie principal suivant i3 pour le cylindre 1. Est-ce parce que l'axe I1 autour duquel on effectue la rotation passe par l'axe entier de notre cylindre numéro 1 ? Et ensuite dans la formule du moment principal pourquoi on ajoute la masse au carré de l'autre cylindre ?
Et enfin dernière question, quand on a un exercice avec un repère donné, je ne parviens jamais à trouvé si l'axe perpendiculaire rentre dans le plan de la feuille ou sort du plan ? On ma donné la regle de la main droite ou la règle des droits mais je ne comprends pas son application ? Désolé si je peux avoir des questions un peu stupide, je suis en école d'ingé et on est bombardé de pleins de matière.. J'adore les sciences et comprendre les choses donc je compte prendre le temps pendant l'été si je n'ai pas trop d'examens de faire de la théorie pure, pour l'instant c'est triste à dire mais j'essaye de trouver des petites recette sans trop comprendre pour faire les exercices...
C'est simplement Pythagore ou à 3 dimensions la norme deEnvoyé par Kanieloutis
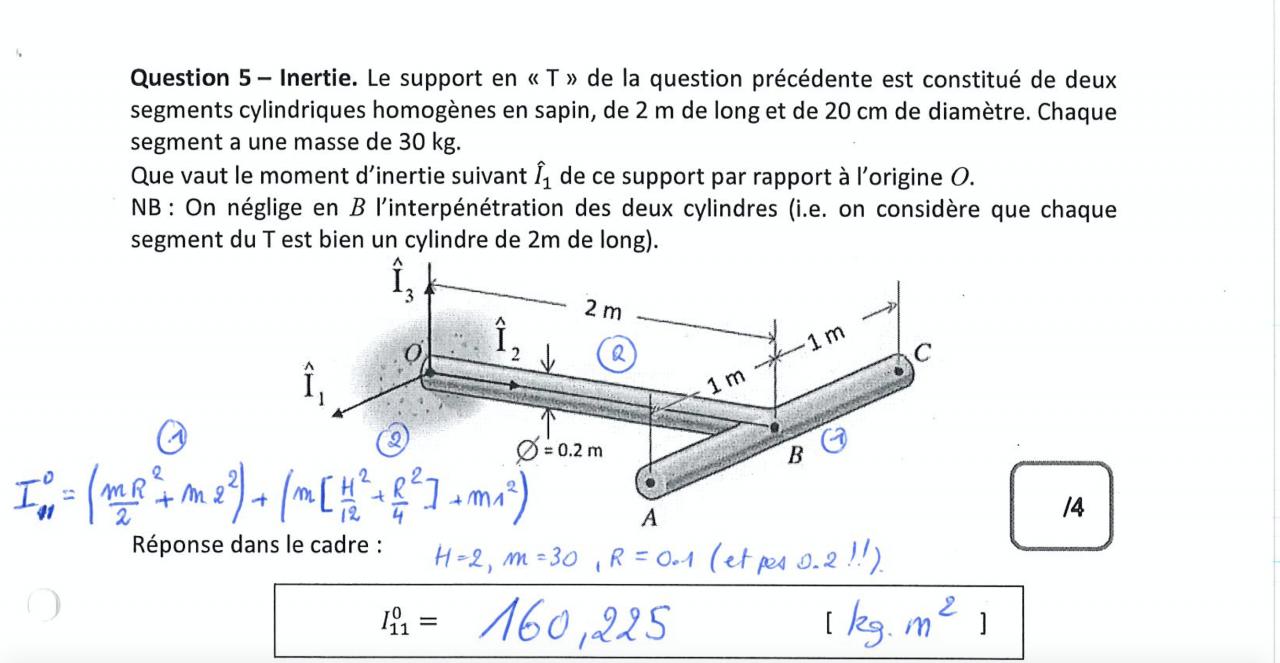
qui est la longueur PG.
Je ne comprends pas la question : les deux moments d'inertie sont pris selon i1. i1 est parallèle à l'axe du cylindre (1) et perpendiculaire à l'axe du cylindre (2), ce sont deux moments d'inertie principaux mais selon deux axes différents.
On n'ajoute pas la masse de l'autre cylindre, c'est toujours Huyghens et la distance du centre à O est de 1m.
C'est le problème des calculs numériques : on ne voit pas ce que l'on fait. Des calculs littéraux puis application numérique sont nettement plus compréhensible/vérifiables ...
Main droite : x = pouce , y = index , z = majeur.
Tire-bouchon : vous tournez de x vers y, le tire-bouchon se déplace dans le sens de z.
Il n'y a pas de questions stupides... Juste un conseil : faites des calculs littéraux.
remarque : si vous pouviez éviter le gras...
Merci énormément monsieur.. je vous suis redevable pour tout l'aide que vous m'apportez depuis le début (c'est toujours vous qui répondez à mes différents topics ^^).
Pour en revenir à la question j'ai bien compris le théorème de Huygens maintenant (ou du moins les grandes lignes), on calcule la matrice d'inertie par à apport au centre de masse du corps et ensuite si on désire l'inertie par apport à un point particulier (P par exemple) du corps, on ajoute à la matrice d'inertie (par apport au Centre de masse) le produit de la masse du corps avec la distance au carré jusqu'au point P.
Ma dernière incompréhension (la question que vous n'aviez pas compris) demeure comment savoir lequel des 3 moments principaux de notre matrice il faut prendre ? Par exemple pour en revenir au problème du cylindre au dessus : on nous demande l'inertie par apport au point O suivant l'axe I1 , commençons avec le cylindre perpendiculaire à l'axe I1, si je prends ma matrice d'inertie principale pour un cylindre (que l'on trouve sur internet mais je met une copie ici) et bien voila comment savoir lequel des 3 moments de la matrice je dois prendre ? Et du coup pareil pour le cylindre parallèle à l'axe I1, dans la matrice d'inertie du cylindre comment savoir quel terme je dois prendre pour faire le calcul ?
Ps : désolé pour le gras j'aurais pensé que cela rendrait plus lisible et moins fatiguant pour les yeux
Je relance ma question
Salut
"l'inertie par apport à un point " ça ne veux rien dire .
Un moment d' inertie , c' est par rapport à un axe .
Pour appliquer Huygens , il faut que les axes soient parallèle .
Si vous raisonnez en matrice d'inertie au point O, le théorème d'Huygens s'énonce :
I(O,m,G) signifiant matrice d'inertie au point d'une masse ponctuelle m en G.
Si vous désirez le moment par rapport à un axe, il faut pour appliquer Huygens, comme l'indique @Dynamix, prendre les deux axes parallèles.
On vérifie bien qu'on ajoute pour Ixx la distance de l'axe parallèle à x passant en O à l'axe parallèle à x passant en G.
