Bonjour,
Dans mes lectures, je suis tombé sur la résolution d'un exercice que je trouve un peu surprenante...
Il s'agit de déterminer la température au centre d'un système cœur-coquille en fonction du temps lors de son refroidissement dans l'air.
Le système de masse m et de capacité thermique massique c est constitué d'une sphère de rayon R1 à la température T1 entourée d'une coquille de rayon R2 à la température T2.
La résolution se fait en deux parties :
1) Conduction thermique de la sphère vers la coquille
-mc dT1/dt = 1/Rth (T1 - T2), où Rth est la résistance thermique du système cœur-coquille
2) Convection dans l'air à partir de la surface de coquille
- mc dT2/dt = h S (T2 - Tair), où h est le coefficient de convection
La résolution numérique des ces deux équations donne T1(t).
Que pensez-vous de ces équations et de cette méthode ? Les équations me semblent fausses...
Il est précisé dans l'énoncé que ce problème peut aussi se résoudre plus classiquement en utilisant l'équation de la chaleur dans les deux milieux et les conditions aux limites mais apparemment la résolution est beaucoup plus complexe...
-----



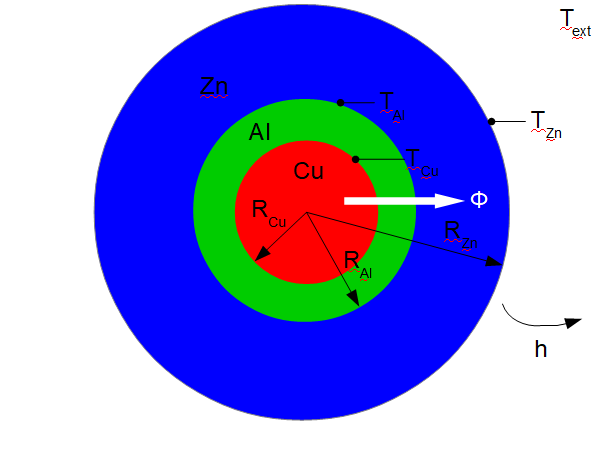 .
. 
 est très petit devant le temps de chauffage (temps caractéristique de l'EDO d'ordre1), cela donne, à la louche (confusion coquille / membrane), en oubliant l'aluminium, et sauf erreur de calcul :
est très petit devant le temps de chauffage (temps caractéristique de l'EDO d'ordre1), cela donne, à la louche (confusion coquille / membrane), en oubliant l'aluminium, et sauf erreur de calcul :