Mécanique des structures - Poutre et barres

[FBMeca]

Bonsoir,

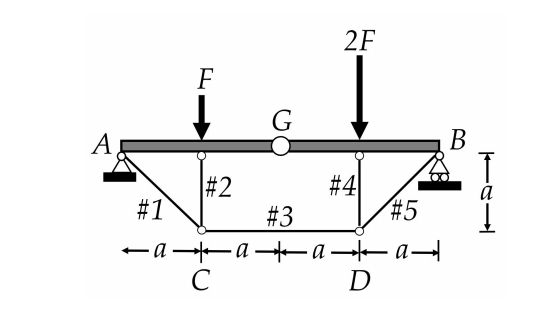
Voici une structure, avec une poutre et des barres en dessous.



J'aimerais trouver les forces internes dans les barres de cette structure. J'ai réussi à le faire en coupant la structure au point G (après avoir trouvé les forces de support), puis en appliquant la somme des moments en ce point précis, et en utilisant les articulations entre les barres pour trouves toutes les forces restantes.

Par contre je ne peux pas appliquer les équations d'équilibre à l'articulation en A pour trouver la force dans la barre #1 par exemple (j'obtiens en conséquence une réponse erronée puisque j'aurais que la force est nulle?!). J'imagine que ceci est dû à la poutre se trouvant là ? Mais pourquoi exactement ? Cela s'applique toujours ?

Je vous remercie d'avance pour votre aide !
-----

[Biname]

Google RDM treillis Cremona. C'est un truc pour calculateur.

Ce cas est simple('a' partout et 45°), il faut d'abord calculer RA et RB. La somme des forces agissant en chaque noeud est nulle. On compose/décompose et on progresse de noeud en noeud. On commence en A puis en B, puis on voit ... Yaka !

?? https://demonstrations.wolfram.com/C...TrussAnalysis/

[FBMeca]

Bonjour,

Je vous remercie pour votre message!
Cela ne répond pas vraiment à ma question. Si j'applique les équations d'équilibre au noeud A, donc sur le support, est-ce que j'ai le droit ? Car pour moi, on a simplement une force verticale, ainsi que la force de la barre #1, ce qui signifierait que la force #1 est nulle, ce qui est bien sûr absurde.

Quel est le problème qu'on a au point A ? Quelle forces est-ce que je suis en train d'oublier?

[Biname]

Bonjour,
Je vous remercie pour votre message!
Cela ne répond pas vraiment à ma question. Si j'applique les équations d'équilibre au noeud A, donc sur le support, est-ce que j'ai le droit ? Car pour moi, on a simplement une force verticale, ainsi que la force de la barre #1, ce qui signifierait que la force #1 est nulle, ce qui est bien sûr absurde.
Quel est le problème qu'on a au point A ? Quelle forces est-ce que je suis en train d'oublier?

Au pied du mur, en A, le maçon décompose mal RA , désolé.

[A voir en vidéo sur Futura]

[Biname]

L'articulation G implique que AB ne fléchit pas, uniquement de la compression.
https://beamguru.com/online/beam-cal...0abc2980f7a3b7
RA=1.25F
RB=1.75F
F#2=F
F#4=2F
F#5=2*F*sqrt(2) (#4 >> #5 et #3)
F#1=F*sqrt(2) (#2 >> #1 et #3)
F#3=3F
Sauf erreur

[FBMeca]

Désolé pour la réponse tardive, merci