Bonjour à tous,
J'espère que le forum "Physique" dans lequel je poste ma demande est adéquat, puisque ma demande concerne un cours de traitement du signal. Voici mon problème :
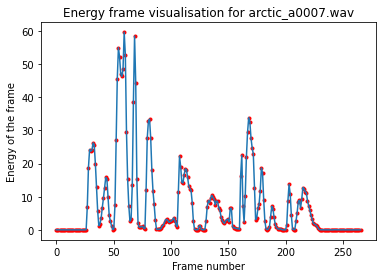
A partir d'un échantillon vocal de quelques secondes, (j'ai une librairie de son que j'appelle aléatoirement allant généralement de 3 à 5 secondes) il m'est demandé de normaliser puis de séparer le tout en fenêtres (par exemple 30ms) avec un pas (par exemple de 15ms). Pour illustrer de manière claire ce contexte, mon signal est numérique et possède une fréquence d'échantillonnage de 16000Hz et j'ai à ce stade une liste de vecteurs "data" correspondant à tous les points, prenant une valeur entre 0 et 1 de 0 à 30ms, puis de 15 à 45ms, puis de 30 à 60ms etc. A partir d'un plot de l'énergie de chaque frame, je demande à l'utilisateur de mon programme d'entrer une énergie seuil à partir de laquelle on considère que des voyelles sont prononcées (je n'ai pas trouvé de moyen peu faillible de rentrer ce seuil automatiquement en n'utilisant que l'énergie de mes frames).
Maintenant que le contexte est bien établi, voici mon problème : il m'est demandé d'utiliser une fonction d'autocorrélation pour chaque fenêtre mon signal numérique afin de déterminer la fréquence fondamentale ("pitch") pour chacune de ces fenêtres, en ne prenant que celles dont l'énergie dépasse le seuil entré par l'utilisateur. N'ayant jamais vu l'autocorrélation en cours, l'enseignant nous a fourni une fonction xcorr.py, laquelle retourne un vecteur "lags" et un vecteur "corr" de taille 101 (je rappelle qu'avec des frames de 30ms et un fs de 16000Hz mes fenêtres sont des vecteurs de taille 480). L'enseignant nous donne également un indice en nous disant, sans expliquer toutefois la fonction, que la distance entre les deux plus hauts sommets de la fonction d'autocorrélation dans le domaine temporel était une bonne approximation de la période fondamentale (1/f0).
J'ai alors utilisé une fonction find_peaks pour trouver les sommets du vecteur "corr" et après un tri, j'ai pu en ressortir les indices de deux plus hauts sommets. En prenant l'inverse de la distance entre ces deux sommets, le tout multiplié par ma fréquence d'échantillonnage afin d'avoir un équivalent temporel me voilà avec un vecteur f0 me donnant la valeur trouvée pour chaque fenêtre. Lorsque je trace tout cela en graphique, catastrophe : je me retrouve avec beaucoup de fenêtres ayant un f0 astronomique (certaines au dessus de 3000Hz, ce qui ne correspond absolument pas à la voix d'un humain (ici j'étudie d'abord une voix d'homme qui plus est)).
En affichant graphiquement le vecteur "corr" je me rend compte en effet qu'avec le bruit du signal, les perturbations peuvent créer des sommets proches du sommet le plus haut et donc fausser les résultats. Cependant même avec quelques astuces du style prendre les sommets du vecteur des sommets afin d'être sûr d'éviter ce genre d'incidents, aucun résultat retournant comme prévu des valeurs proches de disons 150Hz.
Je vous serais infiniment reconnaissant si vous pouviez me donner une piste. Il est fort possible également que mes erreurs soient dues à mon incompréhension de l'autocorrélation, d'autant que prendre la distance entre des points d'un vecteur de 101 points qu'est mon corr, pas sûr que cela vaille la même chose que la distance entre les points de mes fenêtres de 480 points... Je suis dans le flou quant à cela, quant à mon utilité ici du vecteur lags etc.
Je vous remercie d'avance, si vous souhaitez des éléments de mon code (en python) afin de mieux m'aider, je peux vous fournir cela. Désolé du pavé mais il me semble que planter le décor était intéressant pour comprendre mon problème.
-----