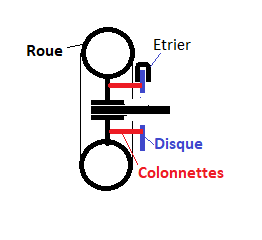
Bonjour,
Je cherche à déterminer les forces de flexion dans chacune des cinq colonnettes fixant ce disque de frein à ma roue (forces initiales supposées nulles en absence de freinage).
Je les soupçonne très inégales et ne parviens pas à les déterminer.
Quelqu'un pourrait-il m'y aider ?
Merci d'avance.
Bonjour ,
Mais c'est quoi cette force de 455N appliquée à cet endroit ? Et la force-poids ?
Le disque est centré par le moyeu . Les puristes vont dire fixation hyperstatique , 4 goujons de trop , un seul travaille , sauf que le disque est serré en 5 points sur le moyeu .
Celui qui accroît son savoir , accroît sa souffrance . L'Ecclésiaste 1-18
Erreur de ma part : pas de force-poids ...
Celui qui accroît son savoir , accroît sa souffrance . L'Ecclésiaste 1-18
Ben, c'est p't être la fatigue, mais je vois plutôt 455 . 55/40, répartis sur les cinq fixations....
Bonjour,
Je suppose les écrous serrés.
Il n'y a pas de flexion, juste de la traction (dans les vis/gougeons) et une transmission par adhérence entre le disque et la roue.
Dans le montage présenté, le disque est déporté de la roue et n'est fixé à celle-ci que par les 5 colonnettes indiquées, sans aucun autre centrage. La force de 455 N est le frottement produit par les plaquettes pinçant le disque en rotation.Envoyé par XK150
En raison de la flexion des-dites colonnettes (proportionnelle aux efforts transmis), on ne peut pas parler de fixation hyperstatique
Surprenant montage ! C'est sur quoi ?
Justement si, et c'est même pour ça qu'on ne peut pas déterminer les efforts. Hyperstatique = plus d'inconnues que d'équations.
On ne peut déterminer la répartition des efforts quand on suppose une rigidité parfaite des liaisons
Ici la flexion inévitable des colonnettes, supposée proportionnelle à l'effort individuel supporté, devrait fournir les équations manquantes.
Je n'ai malheureusement pas encore trouvé lesquelles.
PS: Il s'agit de l'ajout d'un frein de parking sur un ULM "maison"
Dernière modification par harmoniciste ; 30/11/2020 à 20h06.
Lesquels efforts individuels sont indéterminables...
Je comprends mieux
Une expérimentation avec un disque de carton muni de 5 ressorts identiques, auquel une charge serait accrochée au point adéquat permettrait de lever cette "indétermination", et je ne vois pas pourquoi un calcul n'y parviendrait pas aussi bien.
Il me faudra dans les deux cas un certain délai que j'aurais aimé éviter grâce à ce forum.
Bonjour,
L'hypothèse d'une petite déformation proportionnelle à la force doit permettre de résoudre le problème. Il faut remarquer que les forces ne sont surement pas égales et que les moments produits sont en opposition car le point d'application de la force sort du polygone des points de fixation.Il vous faut la somme des forces nulle et la somme des moments nulle.
Les forces seront périodiques à cause de l'angle entre la force de freinage et la position des liaisons, la fréquence sera 5fois le nombre de tours par seconde.
Bonne chance.
Comprendre c'est être capable de faire.
Pas plus que des goujons fixes qui ne sont pas " parfaitement " équidistants engagés dans des trous pas " parfaitement " disposés d'où l'hyperstatisme ,
les ressorts ( les colonnettes ) ne seront pas mieux disposés et " ne travaillerons pas " toutes la même façon .
Au moins , dans le cas , des écrous - goujons , c'est fixation par frottement disque sur moyeu et l'on est tranquille .
Bien sûr , on va augmenter un peu le poids , mais modifier le moyeu rendrait les choses plus faciles à calculer .
Celui qui accroît son savoir , accroît sa souffrance . L'Ecclésiaste 1-18
Les colonnettes étant fixées aux roues par l'adhérence de serrage d'écrous, j'ai donc fait l'hypothèse de contraintes nulle en absence de force de freinage (message#1)
Je suis d'accord en tous points avec phys4: Aucune indétermination et contrainte périodique (mais seul le maxi m'intéresse)
PS: Le but de ce montage tordu est justement de refaire l'atterrisseur pour un accessoire secondaire. Il s'agit d’empêcher la machine de prendre de la vitesse sous la seule traction de l'hélice tournant au ralenti.
Ah, ok, ça complique un peu les choses ça...
Je ne sais pas si vous avez réussi avec cette hypothèse, je vous donne mon résultat à vérifier éventuellement.
Les 5 points d'attache sont situés sur un cercle et forment chacun avec le rayon du frein un angle
Le disque est supposé non déformable, les déformations des fixations ne sont donc indépendantes, de plus nous supposons la déformation négligeables devant les distances des points d'application et nous posons décomposer les déformation en deux parties :
1 - Une rotation da qui produit sur chaque colonne une force tangente k*da
2 - Un déplacement d'un vecteurqui produit donc 5 forces identiques
L'équilibre des forces permet d'écrire que
L'équilibre du couple ramené au centre nos donne
Nous obtenons ainsi la résultante sur chaque colonnettes
Comme le rapport (r0/r1) = 55/40 = 1,375, nous voyons que la résultant est maximale lorsque la colonnette passe en face du frein et s'inverse à la position opposée sans passe par zéro car les deux composantes ne sont pas colinéaires partout.
Il est ainsi possible de calculer la force maximale = (F0/5) (2,375) = 216,175 N
Qu'en pensez vous ?
Comprendre c'est être capable de faire.
Bonjour
Votre résultat confirme le mien, obtenu par simulation avec Exel ou j'observe les efforts vers z et x dus à un soulèvement de z mm et une rotation de alfa degrés, puis en entrant z et alfa par tâtonnements jusqu'à annuler le couple.
Je trouve que dans la position dessinée, l'effort dans les colonnettes 3 et 4 est 45% de F0) tandis que pour la même position, vous trouvez 38%. La différence est due au fait que dans cette position je prend en compte les deux composantes (vers x et z)
Pour la position du maximum d’effort que vous citez, nos résultats concordent(47%)
J'avais craint que ce ne soit beaucoup plus.
Merci, et bravo pour votre méthode bien plus élégante.
