Calculer le temps de demi-vie

[Arelows]

Bonjour,
Je suis en train de faire une annale de biophysique et malgré une correction partiel de l'exercice, je ne comprends pas comment on obtient ce résultat.

Le but de cet exercice est de calculer le temps de demi-vie du 134Cs de deux manières, approximativement et plus précisément.
Je bloque pour la manière approximative (question 3):

1) En explicitant tous les termes, donner:
a) La loi de décroissance radioactive
N=N₀.exp(-lambda x t)
Avec lambda la constante radioactive.
b) La relation entre temps de demi-vie et constante radioactive.
T_1/2=ln(2)/lambda
c) La relation entre le nombre de noyau radioactif N et l’activité A
A=N₀ x lambda

Première méthode (approximative) :
2) De combien est divisée l’activité d’un élément donné au bout de t=T_1/2 et= 2_T1/2?
Pour t=T_1/2:N/N0= 1/2
Pour t= 2T_1/2:N/N0= 1/4

J'ai bien compris ces questions, voici la prochaine sur laquel je bloque:
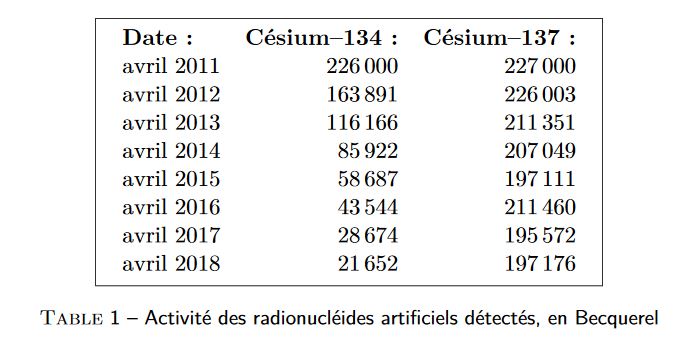
3) partir des données de la table 1, estimer le temps de demi-vie ¹³⁴Cs.


Voici le tableau de données en image
Et la réponse sans justification: 226000/2 = 113000≈116166 soit environ 2 ans
Pouvez-vous m'expliquer pourquoi on divise par deux? Et je ne vois pas en quel unité est le chiffre 116116. J'ai essayée en seconde, minute ou heure mais impossible de trouver comment on en conclut que le temps de demi-vie est de 2 ans au final..

Merci d'avance pour vos réponses,
Bonne soirée
-----

[XK150]

Salut ,

L'activité en 134Cs passe de 226000 le 04/2011 à 116166 le 04/2013 .
Donc , pendant cette durée de 2 ans , vous avez perdu environ la moitié des noyaux pères radioactifs : N/N(0) = 1/2
c'est la définition même de la période T1/2 . T1/2 134Cs = 2 ans ( environ , pour l'exercice )

Si vous cherchez un facteur 4 ( ou plutôt 0.25 de diminution ) vous aurez le temps de 2 périodes T1/2 ...

Vous pourriez faire mieux en exploitant toute la décroissance radioactive ( car votre tableau , c'est l'image de la décroissance radioactive du 134Cs ) ,
sur un graphique en semi-log , mais ce n'est peut être pas l'heure de compliquer ?

[petitmousse49]

Bonjour
Tu as déjà reçu de l'aide concernant ce sujet sur un autre forum...

[jacknicklaus]

116166 n'est pas un calcul, mais l'activité mesurée en avril 2013 (cf table 1). je vous laisse mettre les données bout à bout pour compléter la réponse.

[grillé par 2 réponses. tout le monde s'est donné le mot de répondre au même moment ! ]

[A voir en vidéo sur Futura]

[Arelows]

Tout est clair maintenant ! Je ne sais pas pourquoi je suis resté autant de temps bloqué sur cette question pourtant simple au final
Merci à tous pour votre aide