
- Forum
- Futura-Sciences : les forums de la science
- MATIERE
- Physique
- Problème de raisonnement
Problème de raisonnement
- 27/12/2020, 19h35 #31Liet Kynes
- Date d'inscription
- septembre 2020
- Messages
- 4 999
Re : Problème de raisonnement
------
Sans questions il n'y a que des problèmes sans réponses.
- 27/12/2020, 23h57 #32phys4
- Date d'inscription
- mars 2009
- Localisation
- Ile de France
- Âge
- 82
- Messages
- 9 784
Re : Problème de raisonnement
Excellente de Rachilou au message 26 : la solution la plus petite correspond à une vitesse faible du coureur A, telle que le coureur B le rencontre deux fois alors qua n'a pas eu le temps de parcourir le premier demi-cercle.
Mon approche était effectivement mathématique, elle m'a conduit à poser les équations suivantes, avec t1 et t2 les temps de rencontres.
Equations fixes t1*(v1 + v2) = p t2*(v1 + v2) = 3p
t1*v2 = 40 = p -t1*v1 découle d'une donnée et de l'équation ci-dessus.
Enfin une équation variable pour la seconde rencontre : t2*v1 = 2*n*p +/- 20
avec les deux valeurs possibles n = 0 ou n = 1 et les deux signes possibles seulement si n = 1, ce qui donne 3 jeux d'équations.Comprendre c'est être capable de faire.
- 28/12/2020, 00h12 #33TheaGracias
- Date d'inscription
- octobre 2017
- Messages
- 117
Re : Problème de raisonnement
Merci beaucoup à tous. Xk150 ,oui j'ai remarqué que l'écart de durée n'est plus respecté.

- 28/12/2020, 11h05 #34Black Jack 2
- Date d'inscription
- août 2018
- Messages
- 2 263
Re : Problème de raisonnement
Bonjour,
Il y a 3 triplets (VA, VB; L) solutions distincts.
VB = 4 m/s
premier croisement : 10 s après le départ
deuxiéme croisement : 30 s après le départ
La somme des distances parcourues par les 2 coureurs à l'instant du 2ème croisement est 1,5 L (avec L la longueur de la piste)
En manipulant ces données , on a les contraintes :
L = 80 + 20.vA
30 Va = 20 ou bien 30.VA = L - 20 ou bien 30.VA = L + 20
a)
L = 80 + 20.vA
30 Va = 20
Soit donc VB = 4m/s ; VA = 2/3 m/s et L = 280/3 m
1er croisement après 10 s de course (à 40 m de B et 20/3 m de A, la somme des longueurs = L/2)
2eme croisement après 30 s de course (à 120 m de B et A ayant parcouru 2/3 * 30 = 20 m, la somme des longueurs = 140 m, soit 1,5 L)
b)
L = 80 + 20.vA
30.VA = L - 20
Soit donc : VB = 4m/s ; VA = 6 m/s et L = 200 m
1er croisement après 10 s de course (à 40 m de B et 60 m de A, la somme des longueurs = L/2)
2eme croisement après 30 s de course (à 120 m de B et |6*30 - 200| = 20 m de A, la somme des longueurs = 120 + 6*30 = 300 m, soit 1,5 L)
c)
L = 80 + 20.vA
30.VA = L + 20
Soit donc : VB = 4m/s ; VA = 10 m/s et L = 280 m
1er croisement après 10 s de course (à 40 m de B et 100 m de A, la somme des longueurs = L/2)
2eme croisement après 30 s de course (à 120 m de B et |10*30 - 280| = 20 m de A, la somme des longueurs = 300 + 120 = 420 m, soit 1,5 L)
********
La 1ère de ces solutions (a) est mathématiquement correcte mais VA = 2/3 m/s n'est pas très crédible pratiquement.
La 3ème de ces solutions (c) est mathématiquement correcte mais VA = 10 m/s (pendant 30 s) n'est pas très crédible pratiquement.
Sauf si je me suis planté.
- 28/12/2020, 16h27 #35Liet Kynes
- Date d'inscription
- septembre 2020
- Messages
- 4 999
Re : Problème de raisonnement
Bonjour,
Sur la base de ce schémas:
Pièce jointe 428616
N'est-il pas plus simple de raisonner ainsi: pour arriver en M les deux coureurs couvrent la moitié de la circonférence en faisant un mouvement chacun. de M il repartent une première fois et couvrent la moitié de la circonférence, ils se rencontreront trivialement en ayant couvert toute la circonférence depuis M donc en deux mouvements depuis M.
Comme chaque mouvement du coureur B est de 40 mètres l'écart entre B et P sera de 3*40, celui entre M et P de 2*40 on sais que AP=20 donc la 1/2 circonférence AB est de 3*40+20=140 mètres. On déduis ensuite AM; si AB = 140 et BM = 40 alors AM= 140-40= 100 mètres.
La vitesse du coureur partant de B se calcul en sachant qu'il lui faut 20 secondes pour parcourir MP qui calculé ci dessus MP=2*40=80, vitesse = 80/20=4m/s.Sans questions il n'y a que des problèmes sans réponses.
- 28/12/2020, 18h10 #36Black Jack 2
- Date d'inscription
- août 2018
- Messages
- 2 263
Re : Problème de raisonnement
Bonjour,Bonjour,
Sur la base de ce schémas:
Pièce jointe 428616
N'est-il pas plus simple de raisonner ainsi: pour arriver en M les deux coureurs couvrent la moitié de la circonférence en faisant un mouvement chacun. de M il repartent une première fois et couvrent la moitié de la circonférence, ils se rencontreront trivialement en ayant couvert toute la circonférence depuis M donc en deux mouvements depuis M.
Comme chaque mouvement du coureur B est de 40 mètres l'écart entre B et P sera de 3*40, celui entre M et P de 2*40 on sais que AP=20 donc la 1/2 circonférence AB est de 3*40+20=140 mètres. On déduis ensuite AM; si AB = 140 et BM = 40 alors AM= 140-40= 100 mètres.
La vitesse du coureur partant de B se calcul en sachant qu'il lui faut 20 secondes pour parcourir MP qui calculé ci dessus MP=2*40=80, vitesse = 80/20=4m/s.
Il y a 3 solutions distinctes.
Chacune de ces solutions donne VB = 4 m/s
Mais elles se distinguent par les valeurs de VA et de L (longueur de la piste)
Cela a été mentionné plusieurs fois ... et les valeurs numériques de ces 3 solutions sont données dans le message 34.
- 28/12/2020, 21h48 #37Liet Kynes
- Date d'inscription
- septembre 2020
- Messages
- 4 999
Re : Problème de raisonnement
Je n'en trouve logiquement qu'une, c'est mécanique la vitesse de chaque coureur est constante et détermine la distance parcourue à chaque position AB opposés, M jonction, une position intermédiaire opposée, et une position P jointe.. les valeurs 40 et 20 déterminent un positionnement unique de P. Pour illustrer il est possible de remplacer les coureurs par des aiguilles dans un cadran.Bonjour,
Il y a 3 solutions distinctes.
Chacune de ces solutions donne VB = 4 m/s
Mais elles se distinguent par les valeurs de VA et de L (longueur de la piste)
Cela a été mentionné plusieurs fois ... et les valeurs numériques de ces 3 solutions sont données dans le message 34.Sans questions il n'y a que des problèmes sans réponses.
- 28/12/2020, 22h01 #38TheaGracias
- Date d'inscription
- octobre 2017
- Messages
- 117
Re : Problème de raisonnement
Bonjour à tous. Black jack vous avez donné la priorité à un resultat. Quel est vôtre hypothèse?

- 29/12/2020, 08h58 #39Black Jack 2
- Date d'inscription
- août 2018
- Messages
- 2 263
Re : Problème de raisonnement
On trouve 3 solutions mathématiquement possibles.
Moi qui ne suis pas matheux, cela ne me suffit pas.
Il faut que les solutions correspondent à quelque chose de physiquement raisonnable.
La solution qui fait courir un des coureurs à 10 m/s pendant 30 s est à l'extrême limite du possible (le record du monde du 400 m en 43,03 s et donc 300 m en 30 s n'est réalisable (peut-être) que par très peu d'individus.)
La solution qui fait courir un des coureurs à 2/3 m/s (2,4 km/h) est évidemment possible, mais peut-on appeler cela courir ?
La solution qui fait courir un des coureurs à 6 m/s ... l'autre courant à 4 m/s (obligatoire d'après les données) est par contre tout à fait normale. Ce sont des allures "normales" pour des joggers (un moyen et un bon)
Donc 3 solutions mathématiquement possible et une seule physiquement raisonnable.
- 29/12/2020, 09h02 #40Liet Kynes
- Date d'inscription
- septembre 2020
- Messages
- 4 999
Re : Problème de raisonnement
Je me permet d'insister, car Black Jack propose 3 solutions et je ne vois pas pourquoi, P ne peut que se situer sur deux positions, cependant le mouvement BM étant fixé à 40, L'écart entre M et P ne peut être que de 80 donc Si P après A piste de 2*((3*40)+20)= 280 m et si P avant A piste de 2*(3*40)-20)=200m.
L'écart MP étant toujours de 80 m entre M et P la vitesse du coureur partant de B est dans les deux cas de 80/20=4m/s.
La vitesse du coureur partant de A est pour une piste de 200m : (200-80)/20=6m/s et piste de 280m: (280-80)20=10 m/s
Donc une seule possibilité pour déterminer la distance BA multiplier 3*40 et ajouter 20 ou retirer 20.
La solution a) avec une longueur de piste de 280/3=93.3mètres donc 1/2 circonférence de 93.3/2 ne permet pas au coureur B d'accomplir 40m depuis B pour arriver en M puis 40 m pour arriver en un P distant de 20 m de A.
Ceci étant dans la mesure ou je peux aussi conclure mon raisonnement ainsi ;
;
Je pense que dans le forum maths les spécialistes auraient utilisé l’arithmétique modulaire et parlaient de congruences..Sans questions il n'y a que des problèmes sans réponses.
- 29/12/2020, 09h03 #41Black Jack 2
- Date d'inscription
- août 2018
- Messages
- 2 263
Re : Problème de raisonnement
Et bien tu te trompes. Il y a bien 3 solutions mathématiquement possibles.Je n'en trouve logiquement qu'une, c'est mécanique la vitesse de chaque coureur est constante et détermine la distance parcourue à chaque position AB opposés, M jonction, une position intermédiaire opposée, et une position P jointe.. les valeurs 40 et 20 déterminent un positionnement unique de P. Pour illustrer il est possible de remplacer les coureurs par des aiguilles dans un cadran.
Place donc tes "aiguilles" dans les 3 configurations possibles que j'ai donné et tu verras.
- 29/12/2020, 09h10 #42Liet Kynes
- Date d'inscription
- septembre 2020
- Messages
- 4 999
Re : Problème de raisonnement
Tu peux donner le détail des triplets (VA, VB; L) et comment tu trouves L = 80 + 20.vA
30 Va = 20 ou bien 30.VA = L - 20 ou bien 30.VA = L + 20 ?Sans questions il n'y a que des problèmes sans réponses.
- 29/12/2020, 09h10 #43TheaGracias
- Date d'inscription
- octobre 2017
- Messages
- 117
Re : Problème de raisonnement
Donc Black jack 2. Si les coureurs étaient remplacés par des points mobiles votre raisonnement sera toujours le même?

- 29/12/2020, 09h24 #44Black Jack 2
- Date d'inscription
- août 2018
- Messages
- 2 263
Re : Problème de raisonnement
Rebonjour,Je me permet d'insister, car Black Jack propose 3 solutions et je ne vois pas pourquoi, P ne peut que se situer sur deux positions, cependant le mouvement BM étant fixé à 40, L'écart entre M et P ne peut être que de 80 donc Si P après A piste de 2*((3*40)+20)= 280 m et si P avant A piste de 2*(3*40)-20)=200m.
L'écart MP étant toujours de 80 m entre M et P la vitesse du coureur partant de B est dans les deux cas de 80/20=4m/s.
La vitesse du coureur partant de A est pour une piste de 200m : (200-80)/20=6m/s et piste de 280m: (280-80)20=10 m/s
Donc une seule possibilité pour déterminer la distance BA multiplier 3*40 et ajouter 20 ou retirer 20.
La solution a) avec une longueur de piste de 280/3=93.3mètres donc 1/2 circonférence de 93.3/2 ne permet pas au coureur B d'accomplir 40m depuis B pour arriver en M puis 40 m pour arriver en un P distant de 20 m de A.
Ceci étant dans la mesure ou je peux aussi conclure mon raisonnement ainsi ;
;
Je pense que dans le forum maths les spécialistes auraient utilisé l’arithmétique modulaire et parlaient de congruences..
Tiens voila les 3 solutions détaillées ...
a)
piste de 280/3 m
VA = 2/3 m/s
VB = 4 m/s
Après 10 s de course : A a parcouru 40 m et B a parcouru 20/3 m
La somme des distances (A et B) après 10 s de course = 40 + 20/3 = 140/3 m soit 1/2 longueur de piste ... donc il y a croisement des coureurs.
Après 30 s de courses : A a parcouru 120 m et B a parcouru 20 m
La somme des distances (A et B) après 30 s de course = 120 + 20 = 140 m soit 1,5 longueur de piste ... donc il y a croisement des coureurs. (le 2 ème)
Ce deuxième croisement est bien à 20 m du point B ... puisque le coureur B n'a parcouru que 20 m en 30 s
**********
b)
piste de 200 m
VA = 6 m/s
VB = 4 m/s
Après 10 s de course : A a parcouru 40 m et B a parcouru 60 m
La somme des distances (A et B) après 10 s de course = 40 + 60 = 100 m soit 1/2 longueur de piste ... donc il y a croisement des coureurs.
Après 30 s de course : A a parcouru 120 m et B a parcouru 180 m
La somme des distances (A et B) après 30 s de course = 120 + 180 = 300 m soit 1,5 longueur de piste ... donc il y a croisement des coureurs. (le 2 ème)
Pour ce 2ème croisement, depuis le début, le coureur B a parcouru 30*6 = 180 m ... soit 20 m de moins que le tour complet (et donc il est bien à 20 m du point B)
**********
c)
piste de 280 m
VA = 10 m/s
VB = 4 m/s
Après 10 s de courses : A a parcouru 40 m et B a parcouru 100 m
La somme des distances (A et B) après 10 s de course = 40 + 100 = 140 m soit 1/2 longueur de piste ... donc il y a croisement des coureurs.
Après 30 s de courses : A a parcouru 120 m et B a parcouru 300 m
La somme des distances (A et B) après 30 s de course = 120 + 300 = 420 m soit 1,5 longueur de piste ... donc il y a croisement des coureurs. (le 2 ème)
Pour ce 2ème croisement, depuis le début, le coureur B a parcouru 30*10 = 300 m ... soit 20 m de plus que le tour complet (et donc il est bien à 20 m du point B)
*********
OK ?
- 29/12/2020, 09h29 #45Black Jack 2
- Date d'inscription
- août 2018
- Messages
- 2 263
Re : Problème de raisonnement
Rere bonjour ...
Pourquoi 3 solutions ?
Parce que pour se retrouver à 20 m du point B , le coureur B peut :
a) parcourir seulement 20 m sur l'entièreté de la course
b) parcourir 1 tour complet + 20 m
c) parcourir 1 tour complet - 20 m
- 29/12/2020, 10h11 #46Liet Kynes
- Date d'inscription
- septembre 2020
- Messages
- 4 999
Re : Problème de raisonnement
Ok c'est plus clair, je n'avais pas compris: sur mon schémas je n'ai pas placé et nommé de la même façon, voilà le parcours que tu donnes avec la distance parcourue de 20m pour le coureur (que j'ai nommé a)sur la petite piste avec les aiguilles indicatrices des positions successives:
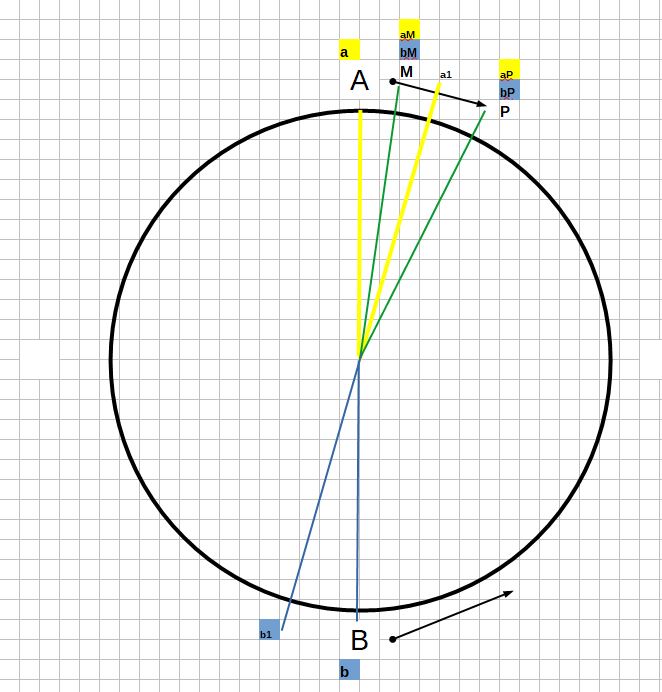 Sans questions il n'y a que des problèmes sans réponses.
Sans questions il n'y a que des problèmes sans réponses.
- 30/12/2020, 21h44 #47invitede656be3
- Date d'inscription
- janvier 1970
- Messages
- 76
Re : Problème de raisonnement
Pas d'intuition, de la méthode, de la méthode et encore de la méthode.
Identifier les inconnues
Fixer des symboles pour les inconnues cohérentes avec les unités
Transformer l'énoncé ( les faits ) en équations en prenant tous les cas possibles
Résoudre les équations si possible.
Voici ce que j'obtiens:
Notations :
R : Rayon de la piste (m)
v1 : Vitesse du coureur 1 partant de A (m/s)
v2 : Vitesse du coureur 2 partant de B (m/s)
t1 : Temps entre le départ et le 1er croisement (s)
t2 : Temps entre le départ et le 2 ème croisement (s)
5 Inconnues R, v1, v2, t1, t2
Les faits :
1er croisement 1 part de A dans le sens horaire, 2 part de B dans l'autre sens donc ils vont forcément se croiser en M.
d’où : distance parcourue par 1 => v1* t1 = Pi * R – 40
distance parcourue par 2 => v2 * t1 = 40
et ils ont fait 1/2 tour => ( v1 + v2 ) = Pi * R
Le 2 ème croisement peux se produire en P1 ou P2, donc 2 cas à prendre en compte
Cas 1 Croisement en P2
distance parcourue par 1 => v1* t2 = 2 * Pi * R – 20
distance parcourue par 2 => v2* t2 = 2 * Pi * R + 20
Cas 2 Croisement en P1
distance parcourue par 1 => v1* t2 = 2 * Pi * R + 20
distance parcourue par 2 => v2* t2 = 2 * Pi * R - 20
De plus t2 - t1 = 20 => (v1+v2) * 20 = distance entre les 2 croisements
On arrive à un système de 5 équations avec 5 inconnues. Il ne s’agit pas d’équations linéaires.
Cas 1
v1 * t1 = Pi * R – 40 (1)
v2 * t1 = 40 (2)
v1 * t2 = 2 * Pi * R – 20 (3)
v2 * t2 = 2 * Pi * R + 20 (4)
t2 - t1 = 20 (5)
Cas 2
v1* t1 = Pi * R – 40
v2 * t1 = 40
v1* t2 = 2 * Pi * R - 20
v2* t2 = 2 * Pi * R - 20
t2 - t1 = 20
Y'a puka fokon resolve
Cas 1
Rapport (3)/(4) et (1)/(2) conduit à R =70 m ou longueur de piste = 439.82 m
Mais il est tard Monsieur il faut préparer le foie pour demain.
- 30/12/2020, 22h04 #48Rachilou
- Date d'inscription
- mai 2011
- Localisation
- De chez moi je vois la tour Eiffel
- Messages
- 613
Re : Problème de raisonnement
EHHH ben !
C 'est bien l'art de se compliquer la vie quand on peut faire tellement plus simplement les choses. La science n'est pas une collection de lois, mais une création libre de l'esprit humain
La science n'est pas une collection de lois, mais une création libre de l'esprit humain
- 31/12/2020, 14h18 #49Black Jack 2
- Date d'inscription
- août 2018
- Messages
- 2 263
Re : Problème de raisonnement
Bonjour,Pas d'intuition, de la méthode, de la méthode et encore de la méthode.
Identifier les inconnues
Fixer des symboles pour les inconnues cohérentes avec les unités
Transformer l'énoncé ( les faits ) en équations en prenant tous les cas possibles
Résoudre les équations si possible.
Voici ce que j'obtiens:
Notations :
R : Rayon de la piste (m)
v1 : Vitesse du coureur 1 partant de A (m/s)
v2 : Vitesse du coureur 2 partant de B (m/s)
t1 : Temps entre le départ et le 1er croisement (s)
t2 : Temps entre le départ et le 2 ème croisement (s)
5 Inconnues R, v1, v2, t1, t2
Les faits :
1er croisement 1 part de A dans le sens horaire, 2 part de B dans l'autre sens donc ils vont forcément se croiser en M.
d’où : distance parcourue par 1 => v1* t1 = Pi * R – 40
distance parcourue par 2 => v2 * t1 = 40
et ils ont fait 1/2 tour => ( v1 + v2 ) = Pi * R
Le 2 ème croisement peux se produire en P1 ou P2, donc 2 cas à prendre en compte
Cas 1 Croisement en P2
distance parcourue par 1 => v1* t2 = 2 * Pi * R – 20
distance parcourue par 2 => v2* t2 = 2 * Pi * R + 20
Cas 2 Croisement en P1
distance parcourue par 1 => v1* t2 = 2 * Pi * R + 20
distance parcourue par 2 => v2* t2 = 2 * Pi * R - 20
De plus t2 - t1 = 20 => (v1+v2) * 20 = distance entre les 2 croisements
On arrive à un système de 5 équations avec 5 inconnues. Il ne s’agit pas d’équations linéaires.
Cas 1
v1 * t1 = Pi * R – 40 (1)
v2 * t1 = 40 (2)
v1 * t2 = 2 * Pi * R – 20 (3)
v2 * t2 = 2 * Pi * R + 20 (4)
t2 - t1 = 20 (5)
Cas 2
v1* t1 = Pi * R – 40
v2 * t1 = 40
v1* t2 = 2 * Pi * R - 20
v2* t2 = 2 * Pi * R - 20
t2 - t1 = 20
Y'a puka fokon resolve
Cas 1
Rapport (3)/(4) et (1)/(2) conduit à R =70 m ou longueur de piste = 439.82 m
Mais il est tard Monsieur il faut préparer le foie pour demain.
Très joli ... mais faux.
Tu as l'air de penser que la somme des distances parcourues jusqu'au 2ème croisement est de 2 tours ... mais que nenni, c'est 1,5 tour (puisque les coureurs partent de points diamétralement opposés)
Et cela corrigé, il te manquera quand même un cas.
Celui où le coureur 1 ne fait que 20 m au total, et le coureur 2 fait 1,5 tour - 20 m
Bonnes fêtes.
- 31/12/2020, 16h07 #50Liet Kynes
- Date d'inscription
- septembre 2020
- Messages
- 4 999
Re : Problème de raisonnement
Quelque part dans ce problème la donnée temps (20secondes) n'est pas importante pour trouver le nombres de solutions possibles concernant les distances, par contre j'aimerai bien avancer plus loin et savoir si l'on peut déduire le nombre de solutions d'une seule équation ?
Sans questions il n'y a que des problèmes sans réponses.
- 31/12/2020, 17h32 #51Rachilou
- Date d'inscription
- mai 2011
- Localisation
- De chez moi je vois la tour Eiffel
- Messages
- 613
Re : Problème de raisonnement
Pour ceux qui ont besoin de visibilité (géométriquement parlant) pour voir si les calculs collent bien.
Du point de vue des distances parcourues:
Dans le sens de l'aiguille d'une montre.
Du point A et B les deux coureurs partent à 180° à l'opposé
Du point M les deux coureurs C1 et C2 partent de 360° à l'opposé (dos à dos si on veux)
M est toujours du même côté. C1 et C2 ne peuvent se croiser que du côté ou il partent.
P est soit en P1 du même côté que M soit en P2 sur le côté opposé.
Donc 4 solutions possibles:
- 1) en P1, le C1 va plus vite que C2
- 2) en P1, le C2 va plus vite que C1
- 3) en P2, le C1 va plus vite que C2
- 4) en P2, le C2 va plus vite que C1 (solution impossible), car si pour le C2 le P2 se situe à 1Tr + 20m alors le point M aurait du se situer à 1/2Tr + 1/3 de 20m ??? donc à l'opposé aussi.
Raisonnement pour n'importe laquelle des 3 solutions :
si le C2 partant de B parcourt 40m à la première rencontre au point M, alors quelque soit le positionnement du point P, le C2 parcourra 80m lors de la deuxième rencontre.
Si il y a 20s entre les points M et P (MP = 80m) alors B va toujours à 4m/s quelque soit la longueur du tour.
Par contre C1 selon les solutions ne peut pas évoluer à la même vitesse.
Résultat des solutions :
- 1) en P1, le C1 cours 200m/20s = 10m/s ,
soit le tour 2(40+80+20) =280m ( point de vue du C2)
- 2) en P1, le C1 cours 13.33m/20s = 0.66m/s ,
soit le tour 2(40+6.66) =93.32m ( point de vue du C2)
- 3) en P2, le C1 cours 120m/20s = 6m/s ,
soit le tour 2(40+40+20) =200m ( point de vue du C2)
Et bonne fête pour ce soir ( en comité restreint)
Dernière modification par Rachilou ; 31/12/2020 à 17h36.
La science n'est pas une collection de lois, mais une création libre de l'esprit humain
- 31/12/2020, 18h00 #52Liet Kynes
- Date d'inscription
- septembre 2020
- Messages
- 4 999
Re : Problème de raisonnement
Merci de ce travail considérable avec des schémas qui ne prennent pas deux minutes à réaliser. Bonnes fêtes à toi également, l'an prochain on enchaîne sur un développement purement théorique de ce problème: j'ai une piste (sans cyclistes) en linéarisant le cercle et projetant la nature du mouvement différemment en fonction des zones segmentaires obtenues..
 Sans questions il n'y a que des problèmes sans réponses.
Sans questions il n'y a que des problèmes sans réponses.
- 02/01/2021, 22h25 #53invitede656be3
- Date d'inscription
- janvier 1970
- Messages
- 76
Re : Problème de raisonnement
Il y a effectivement une erreur de signe sur certaines équations.
Voici la version (en principe corrigée).
Notations :
R : Rayon de la piste (m)
v1 : Vitesse du coureur 1 partant de A (m/s)
v2 : Vitesse du coureur 2 partant de B (m/s)
t1 : Temps entre le départ et le 1er croisement (s)
t2 : Temps entre le départ et le 2 ème croisement (s)
5 Inconnues R, v1, v2, t1, t2
Les faits :
1er croisement 1 part de A dans le sens horaire, 2 part de B dans l'autre sens donc ils vont forcément se croiser en M.
d’où : distance parcourue par 1 => v1 t1 = Pi R – 40
distance parcourue par 2 => v2 t1 = 40
et ils ont fait 1/2 tour => ( v1 + v2 ) t1= Pi R
Le 2 ème croisement peux se produire en P1 ou P2, donc 2 cas à prendre en compte
Cas 1 Croisement en P2
distance parcourue par 1 => v1 t2 = 2 Pi R – 20
distance parcourue par 2 => v2 t2 = Pi R + 20
Cas 2 Croisement en P1
distance parcourue par 1 => v1 t2 = 2 Pi R + 20
distance parcourue par 2 => v2* t2 = Pi * R - 20
De plus t2 - t1 = 20 => 20 ( v1+v2) = distance entre les 2 croisements
On arrive à un système de 5 équations avec 5 inconnues. Il ne s’agit pas d’équations linéaires.
Cas 1
v1 t1 = Pi R – 40 (1)
v2 t1 = 40 (2)
v1 t2 = 2 Pi R – 20 (3)
v2 t2 = Pi R + 20 (4)
t2 - t1 = 20 (5)
Cas 2
v1 t1 = Pi R – 40 (1)
v2 t1 = 40 (2)
v1 t2 = 2 Pi R + 20 (3)
v2 t2 = Pi R – 20 (4)
t2 - t1 = 20 (5)
Cas 1 Croisement en P2
Calcul de L
On fait (3)/(4)
v1 t2 2 Pi R – 20 v1 (3)
------ = --------------- = ------
v2 t2 Pi R + 20 v2 (4)
et
v1 t1 Pi R – 40 v1 (1)
------ = --------------- = -----
v2 t1 40 v2 (2)
donc
2 Pi R – 20 Pi R – 40
---------------- = --------------- => Pi R = 100 L = 200 m
Pi R + 20 40
Calcul de v1
(3 ) - (1) v1 t2 – v1 t1 = 2 Pi R – 20 – Pi R + 40 t2 – t1 = 20
v1 = 6 m/s
Calcul de v2
(2) - (4) v2 = 4 m/s
Calcul de t1 et t2
t1 = 40 / v2 t1 = 10 s t2 = 30 s
On peux vérifier que (3) - (4) donne bien t2 = 30 s
t2( (v1 – v2 ) =2 Pi R – 20 – Pi R – 20
t2 = 30 s
L = 200 m
v1 = 6 m/s
v2 = 4 m/s
t1 = 10 s
t2 = 30 s
Vérification En 10s BM = 4 x 10 = 40 m AM = 6 x 10 = 60 m Somme = 100 m = L/2 OK
Cas 1 Croisement en P2
Par les mêmes calculs on trouve
L = 280 m
v1 = 10 m/s
v2 = 4 m/s
t1 = 10 s
t2 = 30 s
Ce qui recoupe les cas b) et c) de Black Jack 2. Pour le cas a) j’ai un doute sur l'existence de cette solution, a voir.
Ma méthode permet de généraliser l’énoncé à d'autres valeurs. Les variables de départ sont AP = d1 , BM = d2 et T = t2 - t1.
Je pense qu’on peut tout calculer à partir des formules ci-dessus.
Example L = 2 (3 d2 – d1) pour tous les cas.
Et même faire un programme(ou une feuille Excel) qui donne les valeurs à partir des données.
Pourquoi ne pas aller plus loin et voir ce qui se passe pour les croisements suivants. Mais là il faut peut-être aller sur le Forum Math … Sup.
- 03/01/2021, 10h59 #54Black Jack 2
- Date d'inscription
- août 2018
- Messages
- 2 263
Re : Problème de raisonnement
Bonjour,Il y a effectivement une erreur de signe sur certaines équations.
Voici la version (en principe corrigée).
Notations :
R : Rayon de la piste (m)
v1 : Vitesse du coureur 1 partant de A (m/s)
v2 : Vitesse du coureur 2 partant de B (m/s)
t1 : Temps entre le départ et le 1er croisement (s)
t2 : Temps entre le départ et le 2 ème croisement (s)
5 Inconnues R, v1, v2, t1, t2
Les faits :
1er croisement 1 part de A dans le sens horaire, 2 part de B dans l'autre sens donc ils vont forcément se croiser en M.
d’où : distance parcourue par 1 => v1 t1 = Pi R – 40
distance parcourue par 2 => v2 t1 = 40
et ils ont fait 1/2 tour => ( v1 + v2 ) t1= Pi R
Le 2 ème croisement peux se produire en P1 ou P2, donc 2 cas à prendre en compte
Cas 1 Croisement en P2
distance parcourue par 1 => v1 t2 = 2 Pi R – 20
distance parcourue par 2 => v2 t2 = Pi R + 20
Cas 2 Croisement en P1
distance parcourue par 1 => v1 t2 = 2 Pi R + 20
distance parcourue par 2 => v2* t2 = Pi * R - 20
De plus t2 - t1 = 20 => 20 ( v1+v2) = distance entre les 2 croisements
On arrive à un système de 5 équations avec 5 inconnues. Il ne s’agit pas d’équations linéaires.
Cas 1
v1 t1 = Pi R – 40 (1)
v2 t1 = 40 (2)
v1 t2 = 2 Pi R – 20 (3)
v2 t2 = Pi R + 20 (4)
t2 - t1 = 20 (5)
Cas 2
v1 t1 = Pi R – 40 (1)
v2 t1 = 40 (2)
v1 t2 = 2 Pi R + 20 (3)
v2 t2 = Pi R – 20 (4)
t2 - t1 = 20 (5)
Cas 1 Croisement en P2
Calcul de L
On fait (3)/(4)
v1 t2 2 Pi R – 20 v1 (3)
------ = --------------- = ------
v2 t2 Pi R + 20 v2 (4)
et
v1 t1 Pi R – 40 v1 (1)
------ = --------------- = -----
v2 t1 40 v2 (2)
donc
2 Pi R – 20 Pi R – 40
---------------- = --------------- => Pi R = 100 L = 200 m
Pi R + 20 40
Calcul de v1
(3 ) - (1) v1 t2 – v1 t1 = 2 Pi R – 20 – Pi R + 40 t2 – t1 = 20
v1 = 6 m/s
Calcul de v2
(2) - (4) v2 = 4 m/s
Calcul de t1 et t2
t1 = 40 / v2 t1 = 10 s t2 = 30 s
On peux vérifier que (3) - (4) donne bien t2 = 30 s
t2( (v1 – v2 ) =2 Pi R – 20 – Pi R – 20
t2 = 30 s
L = 200 m
v1 = 6 m/s
v2 = 4 m/s
t1 = 10 s
t2 = 30 s
Vérification En 10s BM = 4 x 10 = 40 m AM = 6 x 10 = 60 m Somme = 100 m = L/2 OK
Cas 1 Croisement en P2
Par les mêmes calculs on trouve
L = 280 m
v1 = 10 m/s
v2 = 4 m/s
t1 = 10 s
t2 = 30 s
Ce qui recoupe les cas b) et c) de Black Jack 2. Pour le cas a) j’ai un doute sur l'existence de cette solution, a voir.
Ma méthode permet de généraliser l’énoncé à d'autres valeurs. Les variables de départ sont AP = d1 , BM = d2 et T = t2 - t1.
Je pense qu’on peut tout calculer à partir des formules ci-dessus.
Example L = 2 (3 d2 – d1) pour tous les cas.
Et même faire un programme(ou une feuille Excel) qui donne les valeurs à partir des données.
Pourquoi ne pas aller plus loin et voir ce qui se passe pour les croisements suivants. Mais là il faut peut-être aller sur le Forum Math … Sup.
Aucun doute à avoir sur ma solution a.
L = 80 + 20.vA
30 Va = 20
VB = 4m/s ; VA = 2/3 m/s et L = 280/3 m
1er croisement après 10 s de course (à 40 m de B et 20/3 m de A, la somme des longueurs = L/2)
2eme croisement après 30 s de course (à 120 m de B et A ayant parcouru 2/3 * 30 = 20 m, la somme des longueurs = 140 m, soit 1,5 L)
Au 1er croisement :
Le coureur A a parcouru 20/3 m à la vitesse de 2/3 m/s pendant 10 s
Le coureur B a parcouru 40 m à la vitesse de 4 m/s pendant 10 s
Ensemble, ils ont parcouru la distance de 20/3 + 40 = 140/3 m, soit 0,5 fois la longueur de la piste (de 280/3 m)
Au 2éme croisement :
Le coureur A a parcouru 20 m à la vitesse de 2/3 m/s pendant 30 s
Le coureur B a parcouru 120 m à la vitesse de 4 m/s pendant 30 s
Ensemble, ils ont parcouru la distance de 120+20 = 140 m, soit 1,5 fois la longueur de la piste (de 280/3 m)
C'est enfantin de vérifier que cette solution convient mathématiquement.
Si la mise en équation du problème fait que cette solution n'apparait pas ... c'est que la mise en équation est mauvaise, ou du moins pas complète.
Le cas qui te manque est celui-ci (déjà dit et répété) : c'est le cas où le coureur que tu appelles 1 ne fait que 20 m sur le temps t2.
Cas 2
v1 t1 = Pi R – 40 (1)
v2 t1 = 40 (2)
v1 t2 = 20 (3)
v2 t2 = 3 Pi R - 20 (4)
t2 - t1 = 20 (5)
- 20/01/2021, 15h16 #55invitede656be3
- Date d'inscription
- janvier 1970
- Messages
- 76
Re : Problème de raisonnement
Ok mais il doit y avoir une 4 ème solution. Le 2 ème point de croisement étant symétrique par rapport à AB
Ce qui donne pour les 5 équations
V1t1 = Pi R - d1 (1)
V2t1 = d1 (2)
V1t2 = Pi R + d2 (3)
V2t2 = 2 Pi R - d2 (4)
t2 - t1 = T0 (5)
d1 Longueur arc BM
d2 Longueur arc AP
Ce qui donne Longueur de piste L = 2 Pi R = 3 d1 + d2
V1 = (d1 + d2)/T0
V2 = 2 d1/T0
t1 = T0/2
t2 = 3 T0/2
- 20/01/2021, 16h47 #56Black Jack 2
- Date d'inscription
- août 2018
- Messages
- 2 263
Re : Problème de raisonnement
Bonjour,Ok mais il doit y avoir une 4 ème solution. Le 2 ème point de croisement étant symétrique par rapport à AB
Ce qui donne pour les 5 équations
V1t1 = Pi R - d1 (1)
V2t1 = d1 (2)
V1t2 = Pi R + d2 (3)
V2t2 = 2 Pi R - d2 (4)
t2 - t1 = T0 (5)
d1 Longueur arc BM
d2 Longueur arc AP
Ce qui donne Longueur de piste L = 2 Pi R = 3 d1 + d2
V1 = (d1 + d2)/T0
V2 = 2 d1/T0
t1 = T0/2
t2 = 3 T0/2
Cette solution ne convient pas.
Le 2ème croisement se fait à 20 m de B et pas à 20 m de A.
- 21/01/2021, 22h04 #57invitede656be3
- Date d'inscription
- janvier 1970
- Messages
- 76
Re : Problème de raisonnement
Cette solution ne convient pas.
Le 2ème croisement se fait à 20 m de B et pas à 20 m de A.
Enoncé original :
… ils se croisent une première fois en M à 40m de B, puis une deuxième fois en P à 20m de A. ….
Donc avec mes notations
d1 = Longueur arc BM = 40 m
d2 = Longueur arc AP = 20 m
Les variables d1, d2 et T0 sont là pour généraliser le problème. Cela marche pour un marcheur à pieds, un coureur cycliste, une formule 1 ou un avion de chasse.
En fait c’est un problème de math plutôt que de physique.
En pièce jointe un tableau Excel qui résume les 4 cas.
- 22/01/2021, 10h30 #58Black Jack 2
- Date d'inscription
- août 2018
- Messages
- 2 263
Re : Problème de raisonnement
Bonjour,Cette solution ne convient pas.
Le 2ème croisement se fait à 20 m de B et pas à 20 m de A.
Enoncé original :
… ils se croisent une première fois en M à 40m de B, puis une deuxième fois en P à 20m de A. ….
Donc avec mes notations
d1 = Longueur arc BM = 40 m
d2 = Longueur arc AP = 20 m
Les variables d1, d2 et T0 sont là pour généraliser le problème. Cela marche pour un marcheur à pieds, un coureur cycliste, une formule 1 ou un avion de chasse.
En fait c’est un problème de math plutôt que de physique.
En pièce jointe un tableau Excel qui résume les 4 cas.
Cela devient comique.
Daprès tes calculs la piste mesure 140 m de périmètre.
Le coureur partant de B court à 4 m/s et en 10 s, il a fait 40 m
Le coureur partant de A (dans l'autre sens) court à 3 m/s et en 10 s, il a fait 30 m
Les coureurs se croisent donc pour la 1ère fois à 40 m de B (comme l'énoncé le demande)
Le temps total de course est 10 + 20 = 30 s
Sur ces 30 s, au total le coureur qui est parti de B à fait 30 * 4 = 120 m (1 tour moins 20 m) ... il est donc à 20 m de son point de départ, soit du point B
Sur ces 30 s, au total le coureur qui est parti de A à fait 30 * 3 = 90 m (1/2 tour + 20 m) ... il est donc aussi à 20 m du point B
Le 2éme croisement a lieu à 20 m du point B. (soit à 50 m du point A)
Or l'énoncé IMPOSE pour le 2ème croisement que : "... puis une deuxième fois en P à 20 m de A"
Ta soit-disant 4ème solution ne respecte pas l'énoncé et ne convient pas.
******
Que tu penses que c'est un problème de math plutôt que de physique est ton affaire.
Ici, on a un problème concret avec des contraintes clairement exprimées dans l'énoncé.
Si tu trouves mathématiquement une réponse qui ne convient pas (et c'est facile à vérifier), et bien c'est que ta mise en équation du problème est fausse.
Tu as loupé certaines contraintes imposées par l'énoncé.
Tu peux garder ton point de vue si tu veux, mais cela ne change rien au problème, tu te trompes.
Au lieu de t'acharner sur tes équations avec des oeillères, essaie de comprendre les explications simplistes (comme dans ce message et mon précédent) qui montrent bien que, avec la solution contestée, le 2ème croisement est à 20 m de A et pas à 20 m de B.
... Et quand tu l'auras enfin compris, il sera temps de chercher pourquoi tu t'es planté en mettant ton problème en équation.
- 22/01/2021, 11h37 #59invitede656be3
- Date d'inscription
- janvier 1970
- Messages
- 76
Re : Problème de raisonnement
Désolé j'ai joins un ancien fichier qui comporte une erreur sur le cas N° 4.
Voici le nouveau fichier.
Discussions similaires
-
Equation probleme de raisonnement
Par invite7838e2ab dans le forum Mathématiques du supérieurRéponses: 4Dernier message: 29/04/2018, 22h39 -
Problème de raisonnement mathématique
Par invite3d879c74 dans le forum Mathématiques du supérieurRéponses: 6Dernier message: 15/01/2013, 13h57 -
Problème raisonnement sur exo méca L1
Par invitedc2ff5f1 dans le forum PhysiqueRéponses: 17Dernier message: 12/10/2011, 23h20 -
probleme de math de raisonnement
Par invite8f31e703 dans le forum Mathématiques du collège et du lycéeRéponses: 39Dernier message: 05/11/2007, 13h49 -
j'ai un problème de raisonnement
Par invitea451ee22 dans le forum Mathématiques du supérieurRéponses: 4Dernier message: 04/10/2005, 20h37
Fuseau horaire GMT +1. Il est actuellement 12h51.


