Sommation des forces de pression sur une pyramide

[Venus01]

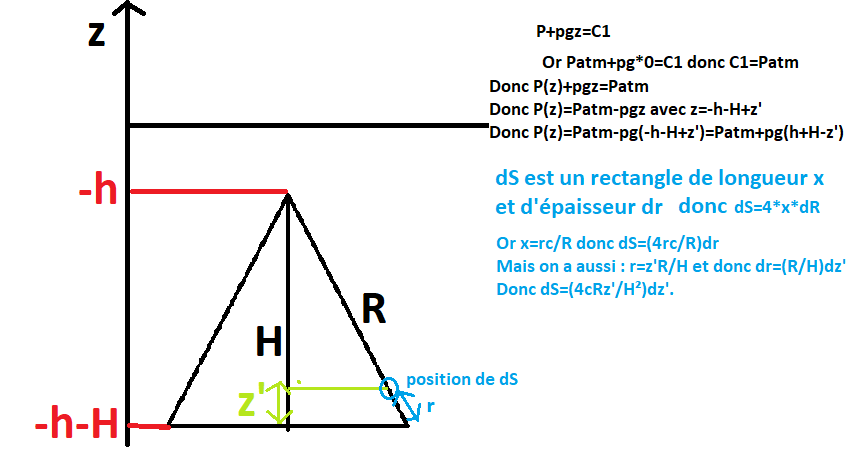
Bonjour, je dois faire un calcul direct par sommation des forces élémentaires de pression pour calculer la force exercée par l'eau sur la surface latérale d'une pyramide immergé dans l'eau (pointe vers le haut avec une épaisseur d'eau h au dessus).
Je pars de dF=-PdS(vecteur n) avec P=Patm+rho.g.(h+H-z'). avec H la hauteur de la pyramide et z' la distance entre la base et un élément de surface dS.
Vu que par symétrie F sera tourner verticale vers le bas, j’écris dF=-PdS.sin(alpha) (vecteur k) car n=sin(alpha)k+cos alpha(j).
Si je ne me trompe pas dS=(4cz'/H)dz' avec c le côté de la base de la pyramide.
En intégrant je me retrouve avec : F=-(2PatmcH+rho.g.c((2H^2/3)+2hH).sin(alpha)k.
Ensuite je suis coincée car j'ai sin(alpha)=c/racine(c^2+4H^2) et en multipliant cela par l'expression précédente je ne trouve pas celle qu'il faut.
En effet je suis censé trouver: F=-c^2[Patm+rho.g((2H/3)+h)]k.
Merci de me débloquer.
-----

[phys4]

Bonjour,
Les équations ne correspondent pas à votre choix de coordonnées, pour avoir une élément dS proportionnel à z', vous auriez du prendre votre origine de z' u sommet de la pyramide, ce qui change l'expression de la pression.
L'intégration sera plus simple de cette manière et devrait vous donner le résultat correct.

[Venus01]

Bonjour,
En effet mon dS est faux. J'ai confondu la hauteur de la pyramide avec la hauteur des faces
Après calcul je prends dS=(4cRz'/H^2)dz' et sin(alpha)=c/2R avec R la hauteur des faces.
En intégrant j'arrive presque au résultat: F=-c^2[Patm+rho.g(h+H/3)]k.
J'ai donc H/3 au lieu de 2H/3.
Je ne sais toujours pas où est mon erreur.
Et désolé mais je ne comprends pas quand vous me dites que j'ai fais une erreur à propos des coordonnées...

[gts2]

Dans le calcul de la surface, z' a comme origine la pointe de la pyramide alors que "P=Patm+rho.g.(h+H-z')" prend comme origine la base de la pyramide (si vous faites z'=0 vous tombez sur rho.g.(h+H)).

[A voir en vidéo sur Futura]

[Venus01]

Je ne comprends pas. Pour moi z' à comme origine la base de la pyramide et z à comme origine la surface de l'eau. Mon axe z est tourner vers le haut.

[gts2]

SI z' a comme origine la base de la pyramide, comment expliquer que l'élément de surface dS, proportionnel à z', soit petit en bas de la pyramide et grand en haut ?

[Venus01]

Ah oui vous avez raison... Mais en regardant ce que j'ai fait je ne vois pas mon erreur.
Je vous joins mon raisonnement pour trouver P et dS...
En tout cas merci pour votre aide

[gts2]

Soit vous changez dS soit vous changez P.

Origine à la base, z' vers le haut, la pression est la bonne, mais l'élément de surface pour z'=0 est dS=c dz' (aux problèmes de projection près) et pour z'=R dS=0, soit dS=c(1-z'/R) dz' toujours aux problèmes de projection près dus au fait que la face est inclinée.

Origine à la pointe, z' vers le bas, l'élément de surface est correct, mais la pression vaut P=P_atm+rho.g.(h+z') : à la pointe (z'=0) on a bien P=P_atm+rho.g.h ; à la base (z'=H) on a bien P=P_atm+rho.g.(h+H)

Aux erreurs de signe et projection près !

[Venus01]

Ah oui merci beaucoup!!!
En effet, grâce à ton explication j'ai trouvé mon erreur de raisonnement. En effet, x n'est pas égale à rc/R mais à c(1-r/R).
Je vais essayer de finir mon calcul pour voir si j'ai le bon résultat.
Merci de votre aide.