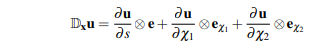Bonsoir,
Je vous écris car je ne suis pas certain de comprendre l'évolution dans le temps du système de coordonnées utilisé dans le modèle de poutre de Timoshenko. En effet, tant qu'on est en statique, tout va bien: on a e qui est le vecteur tangent à la fibre centrale et e_1, e_2 (aussi notés e_ksi_1 et e_ksi_2) qui sont les vecteurs localement associés à une section orthogonale à la fibre. Dans mon cours, on se restreint à une poutre initialement droite.
C'est quand la poutre se déforme que ça se complique. En effet, au cours de la formalisation du principe d'Euler Bernoulli, on écrit, avec s abscisse curviligne, p_G(s) vecteur position à l'instant initial d'un point de la fibre centrale et u(p,t)_G le déplacement à l'instant t du point de la poutre dont le vecteur position est initialement p_G (le long de la fibre); x_G = s*e + u_G(s,t) (le terme s*e vaut en fait p_G(s) car la poutre est droite à l'instant initial). J'en conclus que e ne dépend pas du temps: reste "bloqué" dans sa position initiale. En effet, s'il suivait la déformation de la fibre, on n'obtiendrait pas de la dérivation de cette équation que la tangente au point d'abscisse s est dirigée par: e + d/ds(u_G) mais plutôt que cette tangente serait selon e.
Cependant, lors du calcul du tenseur des petites déformations, on a besoin de la matrice jacobienne du déplacement u. Et là, on fait comme si (e,e_1,e_2) était une base orthonormée : on pose que les colonnes de la matrice sont les dérivées partielles selon s, ksi_1 et ksi_2 et on a:
Et là déjà, ça pose problème car en réalité il faudrait mettre le vecteur tangent à la fibre et non e dans l'expression, mais le plus problématique est à venir.
Puisque e est fixe, j'en conclus que e_1 et e_2 le sont aussi (base orthonormée). Donc e_1 et e_2 ne suivent pas les déplacements des sections orthogonales à la fibre et je trouve ça très curieux car ça complique le repérage des points sur ces sections.
Je pense au contraire que e_1 et e_2 suivent les déplacements de la section orthogonale à la fibre alors que e reste fixe. Et je suppose que l'on approxime (e,e_1,e_2) orthonormée lors du calcul de la jacobienne en supposant les déplacements de la poutre petits.
Ma question est la suivante: Est-ce que je pense juste?
Je vous remercie d'avance pour votre réponse.
Cordialement
-----