Bonjour,
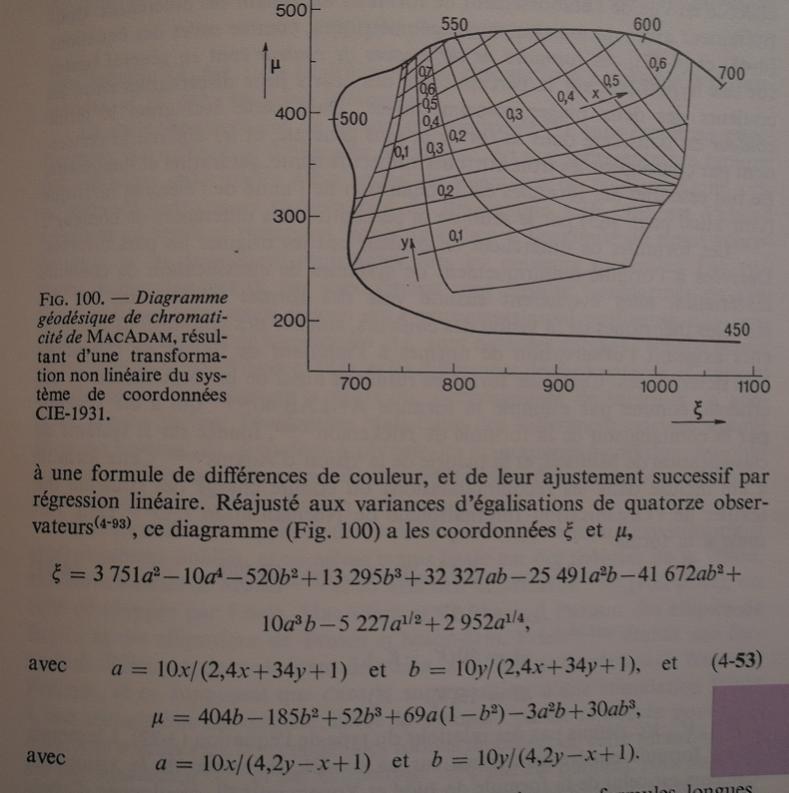
J'ai trouvé dans un vieux bouquin un diagramme de chromaticité que je ne connaissais pas : le diagramme géodésique de MacAdam.
Je voudrais comparer les différences de couleurs que donne ce diagramme avec celles issues des "classiques" L*a*b* et L*u*v*
Malheureusement, le livre ne donne que les formules permettant de passer des coordonnées x, y du diagramme CIE 1931 aux coordonnées ζ, μ du diagramme géodésique, mais pas l'inverse : (ζ, μ) > (x, y)
Je peux donc pour le moment "plotter" des coordonnées CIE L*a*b* ou L*u*v* dans le MacAdam ζ μ, mais pas faire l'inverse!
J'ai essayé de résoudre le système d'équations pour obtenir les solutions pour x et y mais je n'y parviens pas, quelqu'un de plus expérimenté pourrait-il m'aider ?
Voici la formule de xy vers ζμ :
ζ = 3751*a*a-10*a^4-520*b*b+13295*b^3+32327*a*b-25491*a*a*b-41672*a*b*b+10*a^3*b-5227*a^(1/2)+2952*a^(1/4)
avec :
a = 10*x/(2.4*x+34*y+1) et b = 10*y/(2.4*x+34*y+1)
et :
μ = 404*b' - 185*b'*b'+52*b'^3+69*a'*(1-b'*b')-3*a'*a'*b'+30*a'*b'^3
avec :
a' = 10*x/(4.2*y-x+1) et b' = 10*y/(4.2*y-x+1)
Je voudrais donc une solution de calcul qui me donne les coordonnées xy à partir des coordonnées ζμ
est-ce possible?
Merci
-----