Vitesse de remontée d'un ballon dans l'eau

[Amanuensis]

Va falloir expliquer le facteur approximativement 3 entre les deux résultats proposés !
-----

[gts2]

Je n'ai pas posé l'équation différentielle car elle est fausse (*), donc donnera un résultat inexact. Quitte à donner un résultat inexact, autant faire simple.

(*) Car la force de trainée contient, en régime transitoire, un terme lié à l'accélération du fluide (effet de masse ajoutée).

[harmoniciste]

Bonjour,
L'ennui, avec Excel, c'est qu'une erreur de frappe dans une formule passe facilement inaperçue. Maintenant corrigée.
Avec Cx = 1.3 (Large incertitude car gros frottements sur le sac), compter 30 secondes à température constante.

Temps de remontée.ods

Le régime transitoire dont parle gs2 me semble négligeable ici car la vitesse est quasi constante sauf au lacher. Juste mon avis.

[harmoniciste]

car la vitesse est quasi constante sauf au lacher.

PS, Je veux dire l'accélération est très faible.

[gts2]

Confirmation : avec Cx=1,3, je trouve 31 s.

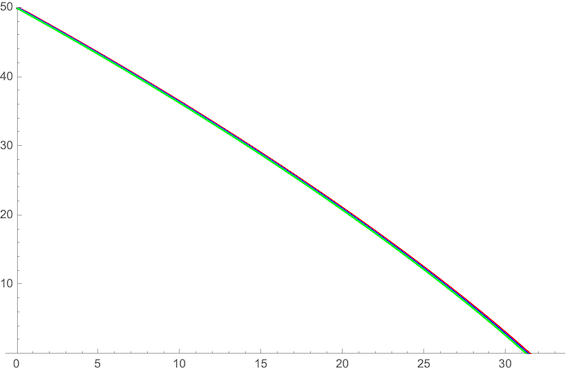
Et la courbe quasi-stationnaire est quasi confondue avec la solution de l'EDO (rouge avec masse ajoutée, bleue sans, vert quasi-stationnaire)

[harmoniciste]

fredney, je constate que le fichier transmis n'est qu'en lecture seule.
Je peux l'envoyer par mail si vous me laissez votre adresse.

[Amanuensis]

Je n'ai pas posé l'équation différentielle car elle est fausse [...] Car la force de trainée contient, en régime transitoire, un terme lié à l'accélération du fluide (effet de masse ajoutée).

Il n'y pas eu d'équa diff explictement proposée. Mais il doit bien y en avoir une telle que l'approximation quasi-stationnaire en soit, de manière démontrable, l'approximation, non? (Aucune justification n'a vraiment été donnée pour le moment, si?)

Ensuite, le régime transitoire n'affecte que le début, non ? Cela doit être bornable. (Borne très petite selon harmoniste, si j'interprète bien.)

[Amanuensis]

Et la courbe quasi-stationnaire est quasi confondue avec la solution de l'EDO (rouge avec masse ajoutée, bleue sans, vert quasi-stationnaire)

Désolé, j'ai zappé ça. Quelques précisions sur l'équation et comme a été obtenue la courbe ?

[Black Jack 2]

Bonjour,
Partant de 20 litres à 50 mètres pour soulever 10 kg, la méthode de Excel (1 ligne toutes les 0.5 s) me donne 60 secondes si Cx = 1,3.
Peu de différence entre Cx = 1 et Cx =1.5
Vitesse ascentionnelle initiale = 0,45 m/s à 50 mètres de profondeur , s'accélérant jusqu'à 1,9 m/s à la surface.

Pièce jointe 439406

Bonjour,

Cx = 1,2 ou 1 ou 1,5 ...
Où vas-tu chercher cela ?

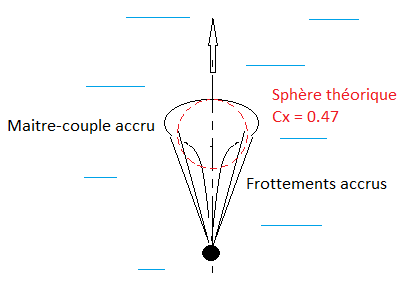
Si le ballon était sphérique, Cx = 0,45 serait la valeur la plus proche.
En forme de poire ... c'est un peu différent (probablement < 0,45)

Mais ce qui importe est le Cx * S
... et le S varie évidemment avec la pression, donc avec la profondeur instantanée.

Quant à la vitesse initiale ... elle est évidemment nulle

Un programme excel avec les données de l'énoncé (20 L à 50 m) et m = 10 kg , donne en adiabatique, un temps de remontée de 18 s environ.

La vitesse initiale est évidemment nulle et la vitesse à l'arrivée en surface est d'environ 3,6 m/s

Ceci avec un Cx = 0,45 et le S calculé (varie avec la profondeur) comme si le ballon restait sphérique (à rayon évidemment variable).
Ce n'est pas exactement ce qui se passe (forme sphérique) ... mais les résultats de temps de montée ne devraient pas être très faux.

Voila ce que cela donne comme graphe (dessiné dans le sens adéquat pour voir la montée vers le haut)




Remarque : si je mets Cx = 1,3 (absurde) dans mon fichier Excel, on arrive aussi à un durée de montée de 30,6 s

[gts2]

J'ai pris pour le terme de masse ajoutée le cas de la sphère en régime laminaire.
Equation différentielle avec terme de masse ajoutée
s1 = NDSolve[{z''[t]*(m + \rho]*V[z[t]]/2) == +m*g + 1/2*\[Rho]*(z'[t])^2*\pi*R[z[t]]^2*Cx - \rho*V[z[t]]*g, z[0] == zi, z'[0] == 0}, z, {t, 0, tmax}]

Equation différentielle sans terme de masse ajoutée
s2 = NDSolve[{z''[t]*m == +m*g + 1/2*\rho]*(z'[t])^2*\pi*R[z[t]]^2*Cx - \rho*V[z[t]]*g, z[0] == zi, z'[0] == 0}, z, {t, 0, tmax}]

Equation différentielle en quasi stationnaire
s3 = NDSolve[{z'[t] == -v[z[t]], z[0] == zi}, z, {t, 0, tmax}]

donne (avec Cx=0,45) t1=18,8s ; t2=18,6s ; t3=18,4s donc le quasi-stationnaire ne marche pas si mal que çà.

[harmoniciste]

Si je mets Cx = 1,3 (absurde) dans mon fichier Excel...

Cx = 0,45 serait une valeur très plausible s’agissant d’une sphère lisse. Mais on est bien loin de ce cas avec le sac de levage de 150 litres n'en contenant que 20: La pression dynamique aplatira la sphère théorique, et étire les bords latéraux, augmentant la surface frontale. Ajoutez à cela la surface constante du sac donnant énorme pourcentage à la trainée de frottement lorsque le volume est encore faible, et mon évaluation grossière de Cx = 1,3 rapportée au diamètre théorique de la sphère parfaite ne me semble pas absurde.
Une Bible des résultats expérimentaux permettant une meilleure compréhension des phénomènes à l’origine de la trainée: "Fluid-dynamique drag" de Sighard Hoerner

[Black Jack 2]

Cx = 0,45 serait une valeur très plausible s’agissant d’une sphère lisse. Mais on est bien loin de ce cas avec le sac de levage de 150 litres n'en contenant que 20: La pression dynamique aplatira la sphère théorique, et étire les bords latéraux, augmentant la surface frontale. Ajoutez à cela la surface constante du sac donnant énorme pourcentage à la trainée de frottement lorsque le volume est encore faible, et mon évaluation grossière de Cx = 1,3 rapportée au diamètre théorique de la sphère parfaite ne me semble pas absurde.
Une Bible des résultats expérimentaux permettant une meilleure compréhension des phénomènes à l’origine de la trainée: "Fluid-dynamique drag" de Sighard Hoerner

Bonjour,

Cx = 1,3 est absurde.

C'est l'ordre de grandeur pour une demi sphère ouverte quand le fluide "entre" dans le creux, comme un parachute semi sphérique pour un saut en parachute d'un avion.

Pour une sphère lisse, Cx = 0,45 est normal.

Dans le cas d'un parachute de remontée, la forme est allongée ... et cela va dans le sens de diminuer le Cx

Piqué sur le net : (un ballon de soulèvement et un petit tableau Cx-forme)



Le Cx est entre celui de la sphère et celui de la forme allongée, ici, on est loin du rapport L/d du dessin du bas ... et donc le Cx est probablement plus proche de celui de la sphère que celui de la forme effilée, mais en tous cas entre les deux.

Certes, il faudrait tenir compte de l'état de surface et ... mais cela va changer peanuts.

Enfin, chacun pense ce qu'il veut.

[Black Jack 2]

Complément à ma réponse précédente :

Non seulement le Cx < 0,45, mais en plus, le maître couple S (section résistant au mouvement) est inférieur à celui de la sphère de même volume.

Et donc calculer avec un Cx * S correspondant à une sphère va dans le sens d'augmenter le temps de remontée.

[harmoniciste]

La forme du sac que vous montrez est celle d'un sac plein. Ce serait donc celle du sac de fredney rempli de 150 litres d'air.
Mais ce même sac rempli de seulement 20 litres, et en montée rapide, aura une forme et des replis qui augmenteront drastiquement le Cx théorique d'une sphère de 20 litres .

[Black Jack 2]

La forme du sac que vous montrez est celle d'un sac plein. Ce serait donc celle du sac de fredney rempli de 150 litres d'air.
Mais ce même sac rempli de seulement 20 litres, et en montée rapide, aura une forme et des replis qui augmenteront drastiquement le Cx théorique d'une sphère de 20 litres .

Pièce jointe 439467

Nous resterons donc en désaccord, je ne te suis pas du tout sur la représentation de ton dessin.

Pour un sac pour faible charge (comme ici), les attaches entre le ballon et la charge sont sur le bas du ballon (pas vrai pour les très grandes charges)



La plupart des ballons ont une forme allongée ... dans le sens du dessin.

Et avec cette forme, le Cx * S sera plus petit que celui de la sphère de même volume.

Mais, comme je l'ai dit, chacun pense ce qu'il veut.

[harmoniciste]

je ne te suis pas du tout sur la représentation de ton dessin.
le Cx * S sera plus petit que celui de la sphère de même volume.

Concernant mon dessin, il ressemble fortement à ça:



Concernant S*Cx
S _{sphère applatie} est plus grande que S non aplatie, et Cx_{sphère applatie} est plus grand que Cx non applatie. Donc S.Cx ne diminue pas, sans parler des frottements supplémentaires.
La trainée dépend
1- des frottements sur les surfaces
2- des décollements de l'écoulement sur la paroi
Il convient de veiller particulièrement ces points, non pas de l'allure générale allongée

[Black Jack 2]

Concernant mon dessin, il ressemble fortement à ça:

Pièce jointe 439531

Concernant S*Cx
S _{sphère applatie} est plus grande que S non aplatie, et Cx_{sphère applatie} est plus grand que Cx non applatie. Donc S.Cx ne diminue pas, sans parler des frottements supplémentaires.
La trainée dépend
1- des frottements sur les surfaces
2- des décollements de l'écoulement sur la paroi
Il convient de veiller particulièrement ces points, non pas de l'allure générale allongée

Cà c'est un ballon avec une armature intérieure sur la partie supérieure.

Ce n'est pas le cas ici avec un "petit ballon de relevage"

L'énoncé précise d'ailleurs : "Dans mon hypothèse, le ballon est extensible à l'infini"

Il se comporte donc comme une baudruche qu'on gonfle plus ou moins.



La forme change peu avec le gonflage, elle reste "allongée" de son Cx*S est forcément inférieur à celui d'une sphère de même volume.

[harmoniciste]

Je comprends que nous ne partons pas des mêmes hypthèses.

Nous pouvons imaginer qu'il s'agit d'un ballon de type stratosphérique, qui n'exerce donc pas réellement de pression lui-même sur le volume contenu et qui a une extension infini sans réellement parler d'élasticité.
par exemple un ballon de 50 litres avec 10 litre d'air injecté à une pression de 5 bars à 50 m il serait donc rempli de 50 litres à la surface.