Vitesse de remontée d'un ballon dans l'eau

[fredney]

Bonjour chers physiciens et mathématiciens.
Je sollicite votre aide, je suis perdu.

J'ai cherché sur le forum et j'ai trouvé une formule que je n'ai pas réussi à mettre en pratique. Il me semble qu'elle est erronée (j'ai des résultats négatifs).
Aussi, je cherche la formule me permettant de calculer le temps de trajet d'un ballon lesté de nKg pour parcourir une montée de x mètres, avec un volume d'air de y litres à une pression z...
Dans mon hypothèse, le ballon est extensible à l'infini donc, il devrait y avoir une exponentielle liée à la profondeur je suppose.
Je ne trouve rien sur Google...
Un exemple de calcul :
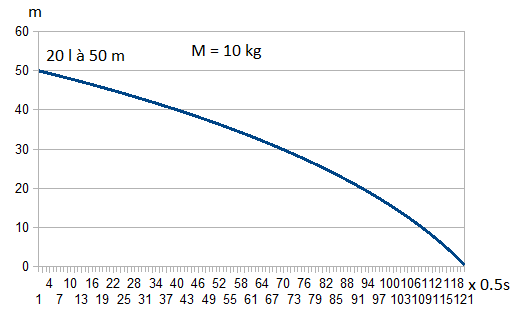
Ballon de 30 litres lesté d'une masse de plomb de 10kg à 50m de profondeur mets xxsec à rejoindre la surface.
La formule me permettrait de faire varier le volume, le poids et la profondeur.

Je vous remercie sincèrement pour votre aide qui m'est précieuse dans le cadre d'un projet professionnel.

Frédéric
-----

[Amanuensis]

En première réaction, il semble manquer au moins une donnée, l'élasticité du ballon, ou encore la fonction liant pression et volume du ballon.

[fredney]

Bonjour,
Nous pouvons imaginer qu'il s'agit d'un ballon de type stratosphérique, qui n'exerce donc pas réellement de pression lui-même sur le volume contenu et qui a une extension infini sans réellement parler d'élasticité.
par exemple un ballon de 50 litres avec 10 litre d'air injecté à une pression de 5 bars à 50 m il serait donc rempli de 50 litres à la surface.

[Amanuensis]

J'imagine que l'application élémentaire de la mécanique donne le résultat souhaité, non ?

C'est à dire l'accélération verticale multipliée par la masse = poids + poussée d'Archimède + frottement ; la poussée étant le volume fois la masse volumique de l'eau, et le volume calculée en fonction de la pression, elle-même fonction de la profondeur. Faut un modèle des frottements fluides ("traînée"), le plus simple (faible vitesse) en opposé de la vitesse.

On obtient une équation différentielle, à intégrer.

Où est la difficulté ? (Autre que l'intégration à faire !)

[A voir en vidéo sur Futura]

[gts2]

j'ai trouvé une formule que je n'ai pas réussi à mettre en pratique. Il me semble qu'elle est erronée (j'ai des résultats négatifs).

Donnez votre formule et votre calcul, pour qu'on puisse confirmer qu'elle est erronée (ou non).
Il y a quand même un certain nombre d'hypothèses/approximations à faire : j'ai cru comprendre qu'on ne tient pas compte de l'enveloppe donc Pgaz=P, qu'en est-il de la température ?

[obi76]

Je ne trouve rien sur Google...

Un début de réponse ici : si vous cherchez des réponses sur cette daube, vous ne mettez pas les chances de votre côté...

[Black Jack 2]

Bonjour,

un volume d'air de y litres ?
Ballon de 30 L ?
le ballon est extensible à l'infini

Pas clair.

Si on a un ballon bien gonflé et quasi indéformable (style ballon de foot ou de basket mais plus grand)

On calcule la poussée d'Archimède (Pa) et le poids propre de l'ensemble ballon + plomb (P)

On estime la vitesse limite de remontée avec :
Pa - P = Fa
Fa étant les frottements aérodynamiques (Fa = 1/2 * Rho(eau) * Cx(sphère) * Pi * (R(ballon))² * v²)

Sauf erreur, avec un ballon sphérique de 30 L et 10 kg de plomb, on arrive à V lim = 2,8 m/s (environ)

et on vérifie qu'avec cette vitesse, l'écoulement est bien turbulent ... ce qui justifie la forme en v² de Fa

La durée de remontée de 50 m est alors d'environ : 50/2,8 = 18 s

La durée d'accélération pour passer de 0 à Vlim est négligeable devant les 18 s.

On peut évidemment faire le calcul complet en résolvant l'équation différentielle : Pa - P - Fa = m.dv/dt ...

Mais c'est inutile si on se contente d'une précision "honnête" sur la durée de remontée, à partir de données du même ordre de grandeur que celles ici.

Aucun calcul vérifié ...

[fredney]

Je tiens à vous remercier TOUS, pour votre implication dans ma demande.
Certaines choses vous semblent plus simple qu'à moi, parce-que nous n'avons pas la même formation. Je suis plus à l'aise avec la mécanique auto, et, avec la cybersécurité par exemple.
Mêmes si certaines choses semblent élémentaires, elles ne me sont pas parvenues naturellement...
Ces réponses me permettent de travailler à valider mon projet.
Merci à tous.

[Amanuensis]

...

Pas regardé en détail, mais j'ai l'impression que le volume a été pris constant ("quasi indéformable"), et non variable avec la profondeur, comme explicitement indiqué.

(Et repris par ma réponse, qui n'a pas été lue.)

Ce qui change pas mal le problème (et donc le résultat).

[Amanuensis]

Pour le modèle à prendre pour la traînée, on peut se baser sur le nombre de Reynolds.

Ici (dans l'eau), en première approximation, on a, en anticipant la vitesse vers 1 m/s : (1 m/s) x (0.1 m) / (10^-6 m²/s) = 10^5, clairement >> 1.

Donc effectivement, contrairement à ce que j'ai écrit, c'est le modèle en v².

[Black Jack 2]

Pas regardé en détail, mais j'ai l'impression que le volume a été pris constant ("quasi indéformable"), et non variable avec la profondeur, comme explicitement indiqué.

(Et repris par ma réponse, qui n'a pas été lue.)

Ce qui change pas mal le problème (et donc le résultat).

Bonjour,

Comme je l'ai indiqué, j'ai bien pris un volume constant pour le ballon.
Et ceci parce qu'il n'y a rien de clair dans l'énoncé sur le volume (je l'ai indiqué spécifiquement)

On donne un ballon de 30 litres avec y litres d'air
Cela veut dire quoi ?

y litres ou 30 litres ? et à quelle pression ?, la pression atmosphérique ou bien à la pression sous 50 m d'eau ?

Bref, on peut répondre avec les conditions désirées ... pourvu qu'elles soient indiquées sans ambiguïté.

Et c'est très très loin d'être le cas.

[fredney]

Le ballon est en fait un parachute de relevage, d'une contenance maximale de 150 litres. L'idée est de lui injecter 0,1nm3 d'air soit, 20 litres à 50m qui deviennent 100litres à la surface.
Sa forme est une "poire"
Précision ici, on utilise de l'eau douce et non de l'eau de mer.

[gts2]

Là, c'est plus clair, il n'y a plus qu'à indiquer votre méthode pour voir où est le problème.

[fredney]

En fait je n'ai pas de méthode justement...
Je sais calculer le volume d'air minimun à injecter à la pression de fond pour décoller cette masse.
Je sais aussi du coup calculer le volume du ballon et sa capacité de levage à la surface...
Donc j'imagine que comme sa "force" de traction évolue durant la montée, on devrait obtenir une courbe du type exponentielle sur la vitesse de remontée. Ainsi, a vitesse constante, il atteint un V limite mais dans mon cas, il semblerait que non. Cela influe donc sur la durée de la remontée.

[gts2]

20 litres à 50m qui deviennent 100 litres à la surface.

Quelle hypothèse prenez-vous pour le gaz ? isotherme donne 120 litres : passage de 6 bars à 1bar.

[Amanuensis]

En fait je n'ai pas de méthode justement...

Donc j'imagine que comme sa "force" de traction évolue durant la montée, on devrait obtenir une courbe du type exponentielle sur la vitesse de remontée. Ainsi, a vitesse constante, il atteint un V limite mais dans mon cas, il semblerait que non. Cela influe donc sur la durée de la remontée.

Oui.

Ayant un tout petit peu d'expérience de plongée (N2) j'avais soupçonné d'entrée que c'était un relevage. Et par expérience aussi, la vitesse augmente tout le temps de la montée.

Et quoi qu'on en dise, c'était suffisamment expliqué message #3.

Je n'ai pas cherché à résoudre l'équa.diff. (avec un v², cela a des chances d'être difficile analytiquement).

Méthode proposée : Poser la formule formelle, et ensuite utiliser un outil informatique (calculateur symbolique -- ou excel comme certains le préconisent !) pour intégrer me semble la bonne approche (du moins c'est ce que ferais -- avec un logiciel de calcul symbolique).

[fredney]

J'ai donc mal calculé le volume final.... Merci pour cette correction.

[fredney]

Ayant un tout petit peu d'expérience de plongée (N2) j'avais soupçonné d'entrée que c'était un relevage. Et par expérience aussi, la vitesse augmente tout le temps de la montée.

Et quoi qu'on en dise, c'était suffisamment expliqué message #3.

Je n'ai pas cherché à résoudre l'équa.diff. (avec un v², cela a des chances d'être difficile analytiquement).

Poser la formule formelle, et ensuite utiliser un outil informatique (calculateur symbolique -- ou excel comme certains le préconisent !) pour intégrer me semble la bonne approche (du moins c'est ce que ferais -- avec un logiciel de calcule symbolique).

merci !
En effet, avec une formule, je pourrais utiliser Excel pour faire varier les différents paramètres (profondeur, volume d'air à x mètres de profondeur, masse du poids) afin de définir une durée "approximative" (pas de prise en charge de la traînée par exemple) de la montée.
Voilà mon but, obtenir une formule me permettant de calculer la durée approximative de la montée selon les paramètres d'entrée, volume d'air injecté en nM3 (tient donc compte de la profondeur), masse à relever, profondeur (distance fond, surface, donnant pression et distance à parcourir).
Le Cx est fixe, la densité de l'eau et de la masse aussi.

[gts2]

La prise en compte de la trainée est obligatoire, sinon arrivé en surface, on aura une accélération de 5g
(au départ mg=kV (Archimède) quasi équilibre, volume multiplié par 6, donc Archimède aussi 6kV-mg=5mg)

Ce qui implique également une vitesse de remontée rapide, donc isotherme ne convient plus.

Je ne suis pas sûr que vous trouviez une formule (simple) t=...

Vous pouvez repartir de l'idée de @Black Jack 2 (message #7) (régime quasi permanent) et calculer vitesse(z) à partir de volume(z), il restera à intégrer ce v(z) pour fabriquer une table.

[fredney]

La prise en compte de la trainée est obligatoire, sinon arrivé en surface, on aura une accélération de 5g
(au départ mg=kV (Archimède) quasi équilibre, volume multiplié par 6, donc Archimède aussi 6kV-mg=5mg)

Ce qui implique également une vitesse de remontée rapide, donc isotherme ne convient plus.

Je ne suis pas sûr que vous trouviez une formule (simple) t=...

Vous pouvez repartir de l'idée de @Black Jack 2 (message #7) (régime quasi permanent) et calculer vitesse(z) à partir de volume(z), il restera à intégrer ce v(z) pour fabriquer une table.

oui, en effet, c'est aussi ce qui me semble le plus logique...
Merci beaucoup !

[Amanuensis]

Ce qui implique également une vitesse de remontée rapide, donc isotherme ne convient plus.

Adiabatique plutôt ?

Volume en p^{-0.7} pour l'air, alors ?

(Volume final de 70 litres (20 x 6^{-0.7}), avec les valeurs numériques indiquée, sf erreur.)

[Black Jack 2]

Rebonjour,

adiabatique (si remontée suffisament rapide pour limiter fortement les échanges de chaleur)

Si 20 L à 50 m de profondeur.

on trouve V(z) = 0,02 * (60/(10+z))^0,7 (environ) (volume du ballon en fonction de la profondeur z)

On en déduit la poussée d'Archimède Pa (en fonction de z)

On connait le poids P de l'ensemble

On calcule Fa la force de frottement aérodynamique (avec forcément des approximations sur la valeur de Cx * S)

On écrit la relation Pa - P - Fa = -m * d²z/dt² (avec z(0) = 50 et dz/dt)(0) = 0) ...

On résout à l'aide d'un tableur par petits incréments de temps.

Sauf erreur (en estimant le Cx * S comme si le ballon restait sphérique en changeant de volume ... ce qui n'est évidemment qu'une approximation)

... on arrive à un temps de remontée de 18,6 s

[fredney]

Rebonjour,

adiabatique (si remontée suffisament rapide pour limiter fortement les échanges de chaleur)

Si 20 L à 50 m de profondeur.

on trouve V(z) = 0,02 * (60/(10+z))^0,7 (environ) (volume du ballon en fonction de la profondeur z)

On en déduit la poussée d'Archimède Pa (en fonction de z)

On connait le poids P de l'ensemble

On calcule Fa la force de frottement aérodynamique (avec forcément des approximations sur la valeur de Cx * S)

On écrit la relation Pa - P - Fa = -m * d²z/dt² (avec z(0) = 50 et dz/dt)(0) = 0) ...

On résout à l'aide d'un tableur par petits incréments de temps.

Sauf erreur (en estimant le Cx * S comme si le ballon restait sphérique en changeant de volume ... ce qui n'est évidemment qu'une approximation)

... on arrive à un temps de remontée de 18,6 s

quelle précision !
Je te remercie sincèrement

[harmoniciste]

Bonjour,
Partant de 20 litres à 50 mètres pour soulever 10 kg, la méthode de Excel (1 ligne toutes les 0.5 s) me donne 60 secondes si Cx = 1,3.
Peu de différence entre Cx = 1 et Cx =1.5
Vitesse ascentionnelle initiale = 0,45 m/s à 50 mètres de profondeur , s'accélérant jusqu'à 1,9 m/s à la surface.

[fredney]

Bonjour,
Partant de 20 litres à 50 mètres pour soulever 10 kg, la méthode de Excel (1 ligne toutes les 0.5 s) me donne 60 secondes si Cx = 1,3.
Peu de différence entre Cx = 1 et Cx =1.5
Vitesse ascentionnelle initiale = 0,45 m/s à 50 mètres de profondeur , s'accélérant jusqu'à 1,9 m/s à la surface.

Pièce jointe 439406

tu as mis quelle formule dans excel ? Un petit copier/coller ?

[harmoniciste]

Bonjour,
Partant de 20 litres à 50 mètres pour soulever 10 kg, la méthode de Excel (1 ligne toutes les 0.5 s) me donne 60 secondes si Cx = 1,3.
Peu de différence entre Cx = 1 et Cx =1.5
Vitesse ascentionnelle initiale = 0,45 m/s à 50 mètres de profondeur , s'accélérant jusqu'à 1,9 m/s à la surface.

Pièce jointe 439406

[fredney]

Bonjour,
Partant de 20 litres à 50 mètres pour soulever 10 kg, la méthode de Excel (1 ligne toutes les 0.5 s) me donne 60 secondes si Cx = 1,3.
Peu de différence entre Cx = 1 et Cx =1.5
Vitesse ascentionnelle initiale = 0,45 m/s à 50 mètres de profondeur , s'accélérant jusqu'à 1,9 m/s à la surface.

Pièce jointe 439406

ah oui, le copier/coller ��
Pas la formule?

[gts2]

Sinon en Mathematica, à transposer :

[fredney]

Mathematica c'est un logiciel?

[Amanuensis]

Mathematica c'est un logiciel?

Oui, un "logiciel de calcul symbolique", de la catégorie que je mentionnais pour traiter (entre autres) des équations aux dérivées, comme celle discutée ici. Les approximations simplificatrice, ou le travail du type ce qui a été fait sur Excel, il le fait bien mieux...

Mathematica c'est excellent, mais cher. Il y en a d'autres, et même des gratuits (comme maxima).

Ils demandent un peu d'apprentissage.

---

gts2 l'a utilisé pour avec l'approximation "quasistationnaire" et une simple intégrale, mais le même outil aurait pu être utilisé en posant directement l'équation aux dérivées, il me semble.