Exercice cinématique

[Geo77b]

La fin de le phrase est "pose problème", problème résolu dans la ligne juste en-dessous :
"Le problème est que pour arriver au centre, le cycliste doit s'appuyer sur le puits or dans le référentiel géocentrique le puits est mobile, ce qui fait que même en absence de frottement, il y a un travail supplémentaire le travail de la force du puits sur le cycliste."
On ne peut donc appliquer la conservation de l'énergie mécanique qui conduisait à l'expression à problème.

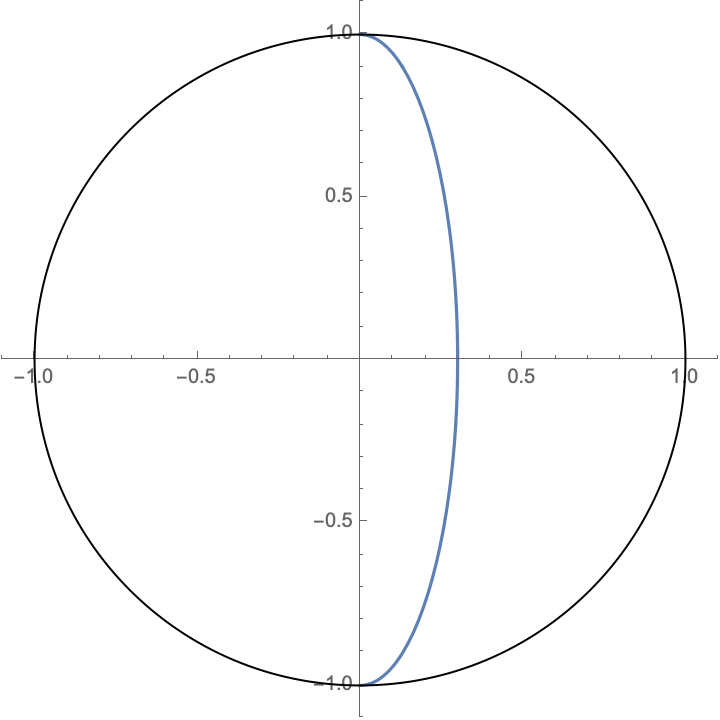
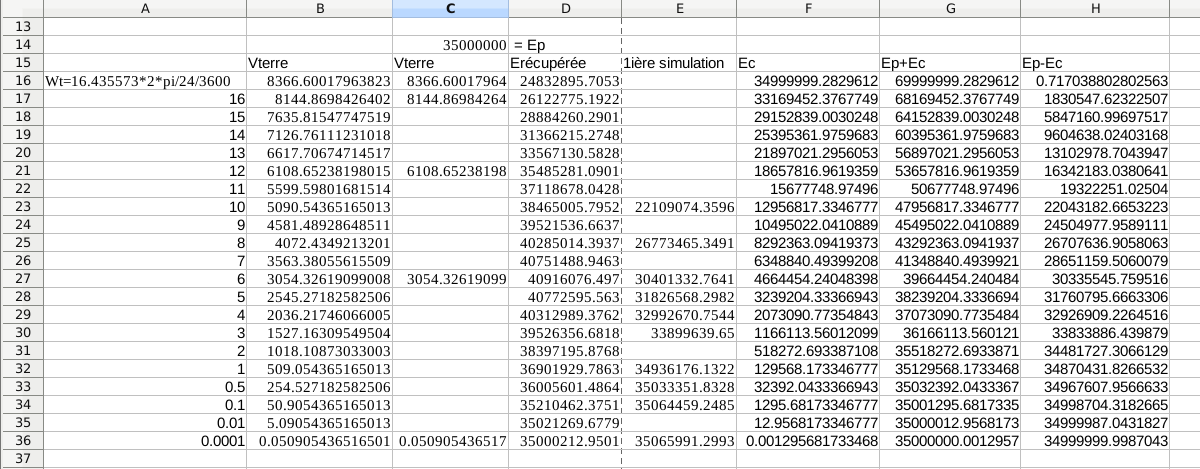
Ca pose problème, ok, mais vous écrivez pour le géocentrique : ???

Non pas suffisante : l'énergie récupérée au centre vaut : , il s'en faut de pour remonter jusqu'à la surface

La soustraction n'est pas la soustraction de l'énergie potentielle et cinétique mais la somme des énergies potentielles de gravitation et centrifuge (message #45)

Ok, mais vous remarquerez que ce sont les mêmes valeurs : Omega^2 R^2 et Vterre^2

Les énergies mécaniques sont fonction du référentiel (il suffit de voir le cas de l'énergie cinétique)

Un ressort comprimé est comprimé de la même façon dans tous les référentiels, c'est quand on transforme l'énergie stockée qu'il y a changement.
Vous vous souvenez probablement de "la fatigue du bonhomme" qui poussait une voiture, laquelle ne variait pas avec le référentiel.
-----

[Geo77b]

Les immeubles se déplacent aussi à cette même vitesse, donc la vitesse du cycliste / immeuble est nulle

Le cycliste remonte radialement dans le référentiel géocentrique, en ligne droite, donc il a une vitesse radiale non nulle, et une vitesse tangentielle nulle, dans ce référentiel.

[gts2]

Ca pose problème, ok, mais vous écrivez pour le géocentrique : ?

Comme on est au centre de rotation, les vitesses dans les deux référentiels sont les mêmes, donc on doit trouver la même énergie cinétique au centre quelque soit le référentiel, le calcul étant plus simple dans le référentiel terrestre, on prend cette expression.

Ok, mais vous remarquerez que ce sont les mêmes valeurs

Au signe près oui, l'énergie cinétique lié à la rotation de la terre est l'opposé de l'énergie potentielle centrifuge.

Un ressort comprimé est comprimé de la même façon dans tous les référentiels

Tout à fait.

[gts2]

Le cycliste remonte radialement dans le référentiel géocentrique, en ligne droite, donc il a une vitesse radiale non nulle, et une vitesse tangentielle nulle, dans ce référentiel.

Oui, mais on a déjà dit que dans ce cas là, il n'atteignait pas la surface.

[gts2]

La solution est un oscillateur harmonique 2D donc en cos(w t + phi) sur les deux axes, ce qui donne (référentiel géocentrique)

et avec .

[Geo77b]

Comme on est au centre de rotation, les vitesses dans les deux référentiels sont les mêmes

Comprend pas ce que ça veut dire.

Au signe près oui, l'énergie cinétique lié à la rotation de la terre est l'opposé de l'énergie potentielle centrifuge.

Omega² R²/2 et Vterre² sont égaux au signe près ?

Epg(R) + m.Omega².R²/2 = m.v0²/2 + Epg(0)

Où passé l'énergie récupérée ?

En fait il (le puit) en consomme en annulant "l'énergie cinétique tangentielle"

L'énergie ne s'annulant pas, à qui revient cette énergie et sous quelle forme ?

[Geo77b]

La solution est un oscillateur harmonique 2D donc en cos(w t + phi) sur les deux axes, ce qui donne (référentiel géocentrique)

et avec .

Pièce jointe 441825

Super. Je vois un oméga et un oméga_0. Oméga_0 est défini, mais qu'est l'autre ?
L'axe des x est vertical ?

[gts2]

Au centre de la terre, la vitesse de la terre est nulle dans le référentiel géocentrique et terrestre, donc pas de vitesse relative, donc la vitesse du cycliste est la même dans les deux référentiels.

L'énergie cinétique vaut 1/2 m Vterre² avec Vterre= \Omega R, et l'énergie potentielle centrifuge vaut -m Omega² R²/2, ce qui est bien l'opposé de l'Ec.

Plutôt que de raisonner en énergie récupérée, je suppose qu'il n'y a pas de frottement et l'énergie récupérée est donc l'Ec m v0^2/2 avec v0 la vitesse au centre.
Vous pouvez donc remplacer m v0^2/2 par Erecupérée

Le travail fourni au puits, qui fait partie de la terre, est donc récupéré par la terre qui voit son énergie cinétique de rotation varier.

[gts2]

Le grand \Omega est celui de la terre.

L'axe des x est vertical au point de départ.

[Geo77b]

Au centre de la terre, la vitesse de la terre est nulle dans le référentiel géocentrique et terrestre, donc pas de vitesse relative, donc la vitesse du cycliste est la même dans les deux référentiels.

Au centre de la terre, la vitesse de la terre est nulle, pourquoi pas.

Plutôt que de raisonner en énergie récupérée, je suppose qu'il n'y a pas de frottement et l'énergie récupérée est donc l'Ec m v0^2/2 avec v0 la vitesse au centre.
Vous pouvez donc remplacer m v0^2/2 par Erecupérée

Avec v0 la vitesse au centre de la terre, qui donc est nulle (voir ci-dessus) et avec Erecupérée = m v0^2/2 ... qui est donc nulle ! Non, décidément, m'y ferai jamais.

Le travail fourni au puits, qui fait partie de la terre, est donc récupéré par la terre qui voit son énergie cinétique de rotation varier.

Quand une pomme tombe d'un arbre (allez, une très grosse pomme), l'énergie de la terre, elle ne varie pas beaucoup, vu le rapport des masses en présence. La bonne nouvelle, c'est qu'on a une autre manip sans puit qui travaille.

[gts2]

v0 est la vitesse du cycliste au centre de la Terre.
La vitesse du centre de la terre / référentiel terrestre est nulle puisque par définition le centre de la Terre est l'origine du repère.

Je n'ai pas dit que l'énergie cinétique de la Terre variait beaucoup, j'ai simplement dit qu'elle variait.

[Geo77b]

Essai de simulation avec les formules de gts2

x = R.cos(w0.t)
y = Wt.R.sin(w0.t)/w0
w0² = g0/R
La trajectoire est tangentielle pour x = 0 = R.cos(w0.t) -> w0.t = PI/2
A ce moment y = Wt.R/w0 = y1
La vitesse avec la dérivée de x en ce point : v1 = w0.R
Synchronisation avec la terre : nouvelle vitesse :
v2 = Wt.y1 = Wt^2*R/w0
Récupération
Et on recommence avec :
v1=v2
R=y1
w0=(g0/R)^.5


Screenshot_2021-06-22_08-14-43.png

[Geo77b]

Les résultats :
On remarquera la ressemblance entre la colonne première simulation et la colonne Ep-Ec (pas si mal).
Pour la nouvelle simulation, on n'est pas loin, mais je cherche l'erreur.

[gts2]

La trajectoire est tangentielle pour x = 0 = R.cos(w0.t) -> w0.t = PI/2
A ce moment y = Wt.R/w0 = y1
La vitesse avec la dérivée de x en ce point : v1 = w0.R

OK : à ce moment, vous êtes quasiment au centre de la terre.

Synchronisation avec la terre : nouvelle vitesse :
v2 = Wt.y1 = Wt^2*R/w0
Récupération

Comment faites-vous la synchronisation ? "Rencontre" avec le puits ?
Qu'entendez-vous par récupération ?

[Geo77b]

OK : à ce moment, vous êtes quasiment au centre de la terre.

A la première répétition, la distance dépend de la vitesse de rotation de la terre (que je fais varier ici pour tester - le cas avec vitesse réelle de la terre se retrouve en face du chiffre 1 de la première colonne des résultats)

Comment faites-vous la synchronisation ? "Rencontre" avec le puits ?
Qu'entendez-vous par récupération ?

Quand la trajectoire est tangentielle, on peut donner un coup de frein, ou mettre un obstacle devant lequel on met un ressort qui va se comprimer, mais il n'y a pas de limite à ce qu'on peut imaginer. Quand le ressort est comprimé, on le bloque dans cette position et on le met de côté pour l'utiliser pour la remontée radiale, qui n'aura pas lieu faute d'énergie à ce qu'il semble.
E récupérée = Ed=Ed+(v1-v2)^2/2

[Geo77b]

OUPS ! J'avais oublié une ligne :

Et on recommence avec :
v1=v2
R=y1
w0=(g0/R)^.5

devient :

Et on recommence avec :
g0=g0*y1/R
v1=v2
R=y1
w0=(g0/R)^.5

et on retrouve les valeurs précises (merci gts2) telles que : Erécuprée = Ep - Ec
Et comme dit au message #48 :

La rotation constitue une sorte de système antigravité. A une certaine vitesse, elle annule la gravité, et elle s'y oppose toujours.
Il serait logique de soustraire l'énergie cinétique (comme dans le repére terrestre comme vous l'avez évoqué).

On retrouve la formule de gts2 pour le référentiel terrestre.
Epg(R) - m.Omega².R²/2

La solution de l'exercice de départ deviendrait donc:
Energie dissipée ou récupérée :
E = énergie potentielle de départ - énergie cinétique de départ (vitesse tangentielle de la terre)
E = intégrale (m.g(h).dh) de la surface à 0 - m.Vterre²/2

Quant à la définition de l'énergie mécanique, ...

[Tolkirum]

Je trouve le problème assez mal posé, et certains commentaires sont contradictoires avec les hypothèses de départ. Si je m'en tiens au premier message, le cycliste démarre avec une vitesse non nulle (notons-la v0) dans le référentiel terrestre, et il la maintient constante. Il arrive donc au centre, avec cette même vitesse, ayant dissipé avec ses freins l'intégrale de 0 à r de l'énergie potentielle de gravitation.
Problème : cette intégrale diverge. Donc l'énergie diverge. La conclusion de ceci semble être : on ne peut pas utiliser l'énergie potentielle pour traiter ce problème.
Une solution : s'arrêter à une distance epsilon non nulle du centre. Soit.
Pour remonter, il faut sans aucun doute utiliser en termes d'énergie l'intégrale d'epsilon à r de l'énergie potentielle de gravitation. Vous voilà donc en haut, avec votre énergie de départ i.e. votre vitesse de départ v0. Choisissez-la orientée comme vous voulez : si le cycliste allait à 20 km/h dans le référentiel terrestre au début de la descente, il ira à 20 km/h à la fin de la remontée.

P.S. Si vous évoquez le moindre "choc" pas vraiment expliqué ni défini avec les "immeubles", ne parlez plus de conservation d'énergie mécanique, c'est absurde.

[obi76]

Problème : cette intégrale diverge.

Pourquoi ? La force de gravitation est d'autant plus faible que l'on se rapproche du centre...

[Tolkirum]

Exact. Elle décroit en 1/r^2, et la fonction 1/r^2 n'est pas intégrale au voisinage de 0.
Version plus physique : l'énergie potentielle associée à la force de gravitation s'écrit sous la forme : cste - mMG/r et donc diverge quand r tend vers 0.

En fait c'est cohérent, la force de gravitation est une force qui diminue "vite" (de façon quadratique) lorsque deux objets se raprochent, donc l'énergie à distance finie r > 0 est infiniment plus grande que l'énergie (pas vraiment définie) à r = 0.

[Geo77b]

Je trouve le problème assez mal posé, et certains commentaires sont contradictoires avec les hypothèses de départ.

Il est vrai que les hypothèses de départ ont un peu évolués pour pouvoir réaliser la simulation, mais le problème est resté similaire.

Si je m'en tiens au premier message, le cycliste démarre avec une vitesse non nulle (notons-la v0) dans le référentiel terrestre, et il la maintient constante. Il arrive donc au centre, avec cette même vitesse, ayant dissipé avec ses freins l'intégrale de 0 à r de l'énergie potentielle de gravitation.

N'oublions pas que la terre tourne.
Au départ, il y a l'énergie potentielle de gravitation + l'énergie cinétique due à la rotation de la terre.
Il ne dissipe avec ses freins, que Ep-Ec, le reste est fourni à la terre via le travail de la force de freinage sur la route (Force x d).

Problème : cette intégrale diverge. Donc l'énergie diverge. La conclusion de ceci semble être : on ne peut pas utiliser l'énergie potentielle pour traiter ce problème.

Je rejoins la remarque de obi76 ci-dessus.

Une solution : s'arrêter à une distance epsilon non nulle du centre. Soit.
Pour remonter, il faut sans aucun doute utiliser en termes d'énergie l'intégrale d'epsilon à r de l'énergie potentielle de gravitation. Vous voilà donc en haut, avec votre énergie de départ i.e. votre vitesse de départ v0. Choisissez-la orientée comme vous voulez : si le cycliste allait à 20 km/h dans le référentiel terrestre au début de la descente, il ira à 20 km/h à la fin de la remontée.

On remonte radialement (dans le référentiel géocentrique), il faudrait donc une énergie égale à Ep pour arriver à la surface, or on ne récupère que Ep-Ec.
En supposant qu'on ait eu assez d'énergie, la vitesse en arrivant à la surface aurait été radiale, et aurait été fonction de la quantité d'énergie utilisée.

P.S. Si vous évoquez le moindre "choc" pas vraiment expliqué ni défini avec les "immeubles", ne parlez plus de conservation d'énergie mécanique, c'est absurde.

Comme la vitesse en arrivant à la surface aurait été radiale, et que, toujours dans le référentiel géocentrique, les immeubles ont une vitesse tangentielle d'environ 510 m/s, le choc était inévitable. Ce choc peut se transformer en chaleur, ou faire l'objet d'une récupération de l'énergie, par exemple via la compression d'un ressort placé de manière convenable. Il s'agissait d'une énergie en "trop", puisqu'on revenait avec la situation de départ et qu'on avait plus d énergie qu'on en avait au départ.

[gts2]

On est à l'intérieur de la Terre et donc le champ est décroissant à fur à mesure que l'on descend (cf. théorème de Gauss).

Avec une approximation grossière (masse volumique constante), on trouve une force linéaire.

[Tolkirum]

J'ai écrit le premier paragraphe du message ci-dessus un peu vite, en me mélangeant moi-même les pinceaux. Comprenez :

La force d'interaction gravitationnelle décroît en 1/r^2, donc on peut exprimer l'énergie potentielle sous la forme, en précisant les grandeurs : cste - mMG/r.
L'énergie potentielle en 0 vaut -oo, et mieux que ça : on ne peut pas intégrer cette expression au voisinage de 0. Autrement dit, la différence d'énergie entre r > 0 et r = 0 est inquantifiable.

[Tolkirum]

Il est vrai que les hypothèses de départ ont un peu évolués pour pouvoir réaliser la simulation, mais le problème est resté similaire.

Bien. Relisez ma réponse en considérant que v0=0... Je fais certes l'hypothèse que le référentiel est galiléen, ce qui n'est pas le cas. Mais c'est précisément ce que vous abordez comme il suit :

N'oublions pas que la terre tourne.
Au départ, il y a l'énergie potentielle de gravitation + l'énergie cinétique due à la rotation de la terre.
Il ne dissipe avec ses freins, que Ep-Ec, le reste est fourni à la terre via le travail de la force de freinage sur la route (Force x d).

Le travail de la force de freinage sur la route ? Rassurez-moi, vous êtes conscient qu'un frein dissipe l'énergie cinétique (sous forme de chaleur ou énergie magnétique) et ne la "transmet" pas ? C'est justement votre idée : faire l'hypothèse que cette énergie peut être récupérée pour propulser le cycliste une fois arrivé en bas, la lui restituant entièrement. Cette idée n'est pas inintéressante, mais ne vous contredisez pas.

L'énergie n'est pas cédée à la Terre : la Terre est ici considérée comme à l'origine d'un champ de gravitation centripète de norme GM/r^2, son énergie à elle est considérée comme constante. Sinon, l'étude est impossible.

Je ne vais pas lire le reste, cela me fatigue pour une simple raison : vous faites des barbarismes à chaque idée que vous introduisez, et cela rend vos idées extrêmement confuses.

Pour conclure :
- on ne peut pas aller jusqu'au centre de la Terre, sinon on oublie le raisonnement énergétique (cf. mon explication plus haut) ;
- l'énergie cinétique du cycliste dans le référentiel géocentrique est égale en permanence à 1/2 * m * r^2 *omega^2, r^2 étant la distance au centre. Cette énergie est élevée au départ, faible lorsque le cycliste est proche du centre (mais pas nulle, cela ne fonctionne pas pour la raison précédente) ;
- admettons que l'énergie perdue soit rendue au cycliste sous une forme purement verticale : OUI, si vous catapultez votre cycliste à la verticale, il partira à la verticale et son énergie cinétique en z=0 correspond à son énergie cinétique au début de l'expérience, autrement dit : la norme de la vitesse (orthoradiale) qu'il avait au départ est égale à la norme de la vitesse (radiale) qu'il a à la fin. Conclusion : il a exactement la même énergie mécanique qu'au début.

[Tolkirum]

On est à l'intérieur de la Terre et donc le champ est décroissant à fur à mesure que l'on descend (cf. théorème de Gauss).

Avec une approximation grossière (masse volumique constante), on trouve une force linéaire.

En effet gts2, je n'avais pas vu les choses comme ça.
(Ma démarche explique précisément les limites du modèle ponctuel pour parler gravitation)

Ceci ne change rien à ce que je viens d'écrire : la différence d'énergie potentielle étant récupérée, on la perd en remontant et on revient à notre énergie cinétique de départ.

[gts2]

Lisez le texte en entier et les réponses aussi :

la Terre est ici considérée comme à l'origine d'un champ de gravitation centripète de norme GM/r^2.

On répète : on est à l'intérieur de la Terre et le champ est approximativement g0 r/R avec g0 = 9,81 m/s2 et R le rayon de la Terre.

On ne peut pas aller jusqu'au centre de la Terre, sinon on oublie le raisonnement énergétique (cf. mon explication plus haut).

Raisonnement correct mais pas avec le bon champ de gravitation.

Edit : messages croisés, cette fois on se comprend.

[Geo77b]

Si vous ne voulez pas lire, il est donc inutile que je vous réponde.

[obi76]

Version plus physique : l'énergie potentielle associée à la force de gravitation s'écrit sous la forme : cste - mMG/r et donc diverge quand r tend vers 0.

Raté, parce que du coup M tend vers 0 aussi (et en R^3...). Effectivement en ponctuel ça diverge, mais là non.

[Tolkirum]

Si vous ne voulez pas lire, il est donc inutile que je vous réponde.

Très bien, tenez : j'ai lu dans ce que vous dites que les freins dissipaient Ep - Ec. Expliquez-moi pourquoi, puisque les freins sont censés freiner le cycliste, et donc dissiper Ec en plus de l'énergie potentielle perdue, d'où une énergie dissipée égale à Ep(r=R) + Ec(initiale).

[gts2]

Très bien, tenez : j'ai lu dans ce que vous dites que les freins dissipaient Ep - Ec. Expliquez-moi pourquoi, puisque les freins sont censés freiner le cycliste, et donc dissiper Ec en plus de l'énergie potentielle perdue, d'où une énergie dissipée égale à Ep(r=R) + Ec(initiale).

Il faut tout lire : dans le référentiel terrestre, on dissipe Ep=Ep(gravitation) + Ep(centrifuge) avec Ep(centrifuge)=
Interprété dans le référentiel géocentrique cette énergie potentielle centrifuge est l'opposé de l'énergie cinétique.

Donc
1- c'est une interprétation, pas un principe physique de base
2- vu que depuis le début, on jongle entre les deux référentiels, il pourrait être utile d'être précis à chaque fois.

[Geo77b]

Très bien, tenez : j'ai lu dans ce que vous dites que les freins dissipaient Ep - Ec. Expliquez-moi pourquoi, puisque les freins sont censés freiner le cycliste, et donc dissiper Ec en plus de l'énergie potentielle perdue, d'où une énergie dissipée égale à Ep(r=R) + Ec(initiale).

Avec plaisir, mais n'étant pas un pro, mes barbarismes,que je reconnais bien volontiers, je ne pourrai pas les éviter, donc ne lisez la suite que si vous pouvez les supporter avec courtoisie.
Si vous tenez à travailler avec v0=0, donc dans le référentiel terrestre, la solution a été donnée par gts2 (message #45) qui pourra sans doute mieux la défendre. Edit : je viens de voir que c'est fait.
Personnellement, je me place dans le référentiel géocentrique, où la terre tourne, avec v0=vitesse tangentielle de la terre (et vitesse relative du cycliste par rapport à la terre=0).
Le cycliste freine, la force exercée se transmet à la roue, qui à son tour excerce une force sur la route (d'où les traces de pneu si on freine fort). Pour freiner, il faut bien s'appuyer sur quelquechose.
Or la route, fixée sur la terre, tourne avec celle-ci dans ce référentiel géocentrique. On a donc une force et une distance parcourue (par seconde), donc une énergie fournie à la terre dans ce référentiel géocentrique où la terre a aussi une énergie cinétique due à sa rotation. Cette part d'énergie n'est donc pas dissipée ou récupérée.
On ne récupèrera que : m.(Vcycliste - Vterre)²/2 , si on synchronise les vitesses (toujours dans le référentiel géocentrique).