succession de qubits

[Adri0]

Bonjour,
La représentation d’un qubit par une sphère de Block est :

sphère de bloch.jpg

Une succession de qubits pourrait elle être représenté comme cela ?:

sup qubits2.jpg
-----

[Deedee81]

Salut,

On pourrait les représenter par plusieurs sphères, une par qbit. Même emboitées.

P.S. Ceci dit je ne comprend pas bien ton dessin (pourquoi les flèches sont colinéaires ??? Les niveaux de complexité c'est la complexité de quoi ??? Apparemment le nombre de qbit envisagé mais c'est bizarre d'appeler ça complexité)

Mais attention, ça c'est pour des qbits indépendants. Ils pourraient être intriqués ou plus généralement dans un état quantique superposé quelconque. Dans ce cas je vois mal comment représenter ça simplement sur un dessin. Mieux vaut utiliser la représentation algébrique avec les kets à la Dirac. C'est simple et clair.

[Deedee81]

Voir par exemple :
https://fr.wikipedia.org/wiki/Notation_bra-ket
https://fr.wikipedia.org/wiki/%C3%89tat_quantique

(mais il y a pas mal de sites qui présentent ça, certains sont sans doutes plus clairs que wikipedia qui n'a pas vocation a être pédagogique)
Je trouve ça pas mal par exemple : http://lptms.u-psud.fr/membres/groux...ationDirac.pdf

Y a des maths mais tout à fait abordable et une une fois qu'on connait on peut beaucoup jouer avec la MQ

[coussin]

Le problème est que "succession", dans ce contexte, ne veut rien dire...

[A voir en vidéo sur Futura]

[Deedee81]

Le problème est que "succession", dans ce contexte, ne veut rien dire...

J'ai juste pris ça comme "plusieurs qbits" (qu'ils soient présents en même temps ou l'un après l'autre, ma foi, ça ne change rien ici)

[Adri0]

@Deedee81

« pourquoi les flèches sont colinéaires »
Je souhaitais exprimer qu’il s’agissait à chaque fois d’un plan différent pour chaque nouvelle sphère, il se réinitialise pour en créer un nouveau prenant en compte l’état précédant et évolue avec une croissance généré par les toutes réponses possibles à cet état, une fois trouvées il réitère l’opération.
J’imagine (probablement à tord) la Compléxité d’un problème étant toutes les réponses possibles audit problème. Ainsi à chaque transfert d’un système vers un autre système, la Complexité passe au niveau suivant.

Merci pour le partage des liens sur le sujet.

@coussin

Désolé, totalement néophyte sur le sujet…

[Deedee81]

Salut,

« pourquoi les flèches sont colinéaires »
Je souhaitais exprimer qu’il s’agissait à chaque fois d’un plan différent pour chaque nouvelle sphère, il se réinitialise pour en créer un nouveau prenant en compte l’état précédant et évolue avec une croissance généré par les toutes réponses possibles à cet état, une fois trouvées il réitère l’opération.

D'accord, un peu comme des axes. Ceci dit, cette idée de croissance ne me semble pas particulièremen

Désolé, totalement néophyte sur le sujet…

Toit s'apprend

Mais avant de jouer avec les représentations, il est sans doute préférable de savoir "pourquoi représente-t-on le q-bit comme ça" et "quelle est la signification physique de ce genre d'état physique". Et donc il est sans doute préférable de commencer par un peu de théorie (la MQ c'est vaste, très vaste, et compliqué.... mais en se limitant aux bases, aux notations avec des kets... ça va encore, c'est tout à fait abordable)

[Adri0]

Deedee81


J’ai lu tout ce que vous m’avez envoyé, je doit vous avouez ne pas en comprendre une grande partie... du coup je suis entrain de faire une relecture « fractionné » par des recherches pour combler les lacunes (Et il y en a un paquet) mais comme vous dites « tout s’apprend ».

Pour moi la sphère de Bloch représente le champ généré par les deux états de base, un peu comme si une explosion avait lieu et que son onde de choc ne rencontrai aucun objet, cela formerai une sphère dont la totalité de la paroi est la réponse visuelle au champs d’influence de l’explosion, du coup lorsque que l’on « choisit » une réponse (un point sur la paroi) que l’on nomme |0> ; son inverse |1> est « obligé » d’exister pour exprimer le champs de ces deux états, d’où la sphère..

Désolé si c’est pas très clair… mais le sujet me fascine autant qu’il me trouble je dirai !
(Pardon pour ce coté plus philosophique, probablement une vision simpliste, mais je me suis dit du coup qu’une chose ne pouvait pas exister sans son contraire)

Je vais continuer à lire !

[Deedee81]

Pour moi la sphère de Bloch représente le champ généré par les deux états de base

L'état (quantique), pas le champ (champ a une signification précise qui ne s'applique pas ici).
Et généré est un peu impropre, il est mieux de dire "obtenu par superposition (quantique) des deux états de base"
(et le fait que c'est une sphère est dû au fait que les coefficients de pondérations de la superposition sont des nombres complexes + la condition de normalisation + une phase arbitraire qu'on peut ignorer)

EDIT ça fait 2*2-2 paramètres pour la superposition et il se fait que les 2 paramètres restant se représentent de manière commode comme une sphère. C'est juste la formulation mathématique qui autorise cette représentation assez commode.

un peu comme si une explosion avait lieu et que son onde de choc ne rencontrai aucun objet, cela formerai une sphère dont la totalité de la paroi est la réponse visuelle au champs d’influence de l’explosion

Holà non !!!! C'est pas une explosion, ni même "comme si". Et d'ailleurs le diamètre de la sphère est totalement arbitraire (on prend un rayon de 1 pour respecter la normalisation).

La sphère de Bloch n'est pas un "processus physique sphérique", c'est juste une représentation, un graphique. Tout comme un graphique des températures n'est pas "des températures qui ont coulé sur une feuille" !!!!

du coup lorsque que l’on « choisit » une réponse (un point sur la paroi) que l’on nomme |0> ; son inverse |1> est « obligé » d’exister pour exprimer le champs de ces deux états, d’où la sphère..

Là je n'ai pas compris mais ça découle certainement de l'erreur précédente.

(Pardon pour ce coté plus philosophique, probablement une vision simpliste, mais je me suis dit du coup qu’une chose ne pouvait pas exister sans son contraire)

Non, ni philosophique ni simpliste. C'est juste erroné : la sphère c'est juste un dessin, il n'y a aucune sphère dans le phénomène physique considéré. Tout comme il n'y a pas de "feuille plane" dans les températures de la journée.

[Adri0]

yep, merci pour les éclaircissements cela me dépasse, je vais continuer à lire..

[Adri0]

« ça fait 2*2-2 paramètres pour la superposition »
Désolé de vous embêter avec ça mais connaîtriez vous un papier décrivant cela, je ne comprend pas…

Je me suis fait, il y a un moment, ces représentations du transport d’état d’un qubit sur un autre qubit :

superposition.jpg

superposition sphère de boch.png

[Adri0]

probablement fantaisiste..

[Deedee81]

Salut,

« ça fait 2*2-2 paramètres pour la superposition »
Désolé de vous embêter avec ça mais connaîtriez vous un papier décrivant cela, je ne comprend pas…

C'est pas bien compliqué.

https://fr.wikipedia.org/wiki/Sph%C3%A8re_de_Bloch
et un peu plus ici sur la description de l'état quantique correspondant
https://fr.wikipedia.org/wiki/Qubit#...#39;%C3%A9tats

probablement fantaisiste..

Surtout totalement incompréhensible (peut-être fantaisiste mais comment le savoir puisqu'on ne peut même pas comprendre ta représentation)

[Adri0]

« Surtout totalement incompréhensible (peut-être fantaisiste mais comment le savoir puisqu'on ne peut même pas comprendre ta représentation) »

Désolé…
Je me permets d’écrire comment j’ai compris les lectures que vous m’avez soumis.
Si vous pouviez jeter un œil et m’aiguiller sur les erreurs… merci d’avance !

un qubit, peut être représenté par un point sur une sphère de Bloch.
Avant mesure, l’état d’un qubit est une superposition quantique linéaire de ses deux états de base qui algébriquement donne ceci : α ∙ |0› + β ∙ |1›
Et géométriquement est une position sur la sphère de Bloch, sphère qui permet de visualiser graphiquement le vecteur représentant toutes les positions possibles résultantes de cette superposition.
La mesure permet de déterminer les coordonnées cartésiennes du point sur la sphère par projection sur un des vecteurs de la base, ce qui fait qu’il ne peut être dupliqué après mesure.

Pour ce qui est de ma représentation, c’est sur que si c’est incompréhensible on ne peut pas déterminer si c’est fantaisiste : ) il faut donc que j’améliore ma compréhension sur le sujet et également ma façon d’exposer des idées. (Les deux vont probablement ensembles d’ailleurs..). Je vais essayer travailler dans ce sens là.

Je m’essayais à l’idée simulant les paramètres pour la superposition comme pouvant être
2*2-2 et (2+2)/2 soit toujours deux paramètres restant. Mais quatre en tout.

Un état initial :

x + x = x * x avec x = 2

D’où découlerait les deux paramètres possibles pour la superposition (les solutions possibles à l’état initial)

x = x * x – x soit 2*2-2
et
x = (x+x)/x soit (2+2)/2

avec deux paramètres restant par solution :
|0› = 0 et |0›=1
|1› = 1 et |1›=0

En espérant être plus clair…

[Sethy]

Au feeling ...

S'il faut une sphère de Bloch pour représenter correctement un qubit, sphère qui est par essence un objet à 2 dimensions "plongé" dans un espace de degré supérieur (3 ici) pour "prendre tout son sens" (ndlr : à reformuler), ne faut-il pas des espaces à 2n-dimensions pour représenter un ensemble n de qubits et lui aussi plongé dans un hyper-espace d'ordre "encore" supérieur ?

Autrement dit, pour un 2-qubit ne faut-il pas un représentation de dimension 4 qui "engendrerait" une hypersphère d'ordre 5 ou même 6 ?

La page wiki en anglais me semble assez claire, je cite : "In general, n qubits are represented by a superposition state vector in 2n dimensional Hilbert space.". Source : https://en.wikipedia.org/wiki/Qubit

[Sethy]

Plus généralement, je pense que tu ne vois pas que ton espace n'est pas assez "riche" pour contenir un 2-qubit (ou plus d'un qubit).

Voici en image, le problème. Pour simplifier, j'imagine qu'on pourrait représenter le qubit par un cercle. C'est faux bien sûr, mais le problème est le même en 3 dimensions, donc autant s'éviter les complications inutiles.

En deux dimensions, selon la représentation que tu adoptes, cela pourrait donner ceci :

L'ensemble des qubits possibles se trouverait sur le cercle :

Q1.JPG

et un qubit en particulier, qui est justement le cas particulier que tu prends pourrait être représenté ainsi :

Q2.JPG

Mais le second qubit ne devrait pas être représenté comme tu le fais, mais plutôt comme ceci. C'est à dire comme un second cercle qui est centré sur la position du premier :

Q3.JPG

En choisissant à nouveau une position "privilégiée", cela donne le même résultat que toi :

Q4.JPG

Oui mais ... ça ne fonctionne que parce que tu as choisi un cas particulier. Dans le cas général, le qubit se trouve à une position quelconque du cercle. Et c'est à partir de ce point qu'il faut centrer le "départ" du 2ème qubit, comme ici :

Q5.JPG

(suite au prochain post, limité à 5 pièces jointes)

[Sethy]

(suite)

En choisissant une nouvelle position quelconque on obtient ceci :

Q6.JPG

Et c'est là que le bât blesse. Car si sur une seule sphère (ici un cercle mais c'est pareil), à une position précise sur le cercle ne correspond qu'une seule valeur de alpha et de bêta (ce qui caractérise totalement le qubit), ici avec un 2-qubit, à une position de l'espace correspond à 2 possibilités distinctes :

Q.JPG

Ici, on le voit bien : Il n'est pas possible de distinguer si le qubit 1 est dans le cas orange ou dans le cas bleu (Situation 1 ou 2).

Mathématiquement il ne s'agit plus d'une bijection, comme dans le cas de la sphère de Bloch associée à un qubit. La bijection est contraignante dans les deux sens. A un qubit particulier (caractérisé par alpha et bêta) correspond 1 et 1 seul point sur la sphère de Bloch. Et à un point de la sphère de bloc ne correspond qu'un et un seul qubit.

Ici, au contraire, il n'y a plus bijection puisqu'un même point de l'espace correspond à plusieurs possibilités pour les 2-qubits.

Note : le cas Situation 1 + 2 n'est là que pour montrer que le point "solution" est bien le même dans les deux cas.

[coussin]

Tout a été dit au message #15.
Si l'état d'un qubit vit sur la surface de la sphère de Block c'est parce que cet état possède 2 degrés de libertés, les 2 coefficients de décomposition sur |0> et |1> (oublions pour l'instant que ces coefficients sont complexes...)
2 qubits possède 4 degrés de liberté, les 4 coefficients de décomposition sur |00>, |01>, |10> et |11> et cet état vit sur une hypersurface de dimension 4 qui ne peut pas être représentée...
Et ainsi de suite pour n qubits...

[Deedee81]

Salut,

Adri0, pas de problème, c'est un peu brouillon, ça rend la lecture difficile, mais ça m' l'air juste.

Sethy, coussin. Je suis d'accord avec tout ça, c'est la difficulté de représentation que j'avais soulevé tout au début si "les deux q-bits ne sont pas indépendants".
(c'est encore pire si les objets quantiques sont indiscernables mais au moins pour des qbits, la séparation spatiale est suffisante pour parler d'objets discernables, mais ce n'est qu'une bien maigre simplification, et imaginez qu'ils ne soient pas discernables et plongés dans une superposition quantique d'espace-temps courbés... non, là c'est moi qui pète une durite )

Je pense qu'on ne peut pas obtenir de représentation graphique de plusieurs qbits sans :
- ou bien perdre une partie de l'information
- ou bien avoir un truc imbuvable (genre représentation à N dimensions et de nombreuses coupes à 2D comme pour un plan d'architecture ou d'ingénieur, ça peut vite devenir épouvantable)

Allez, une petite blague (que j'avais déjà cité auparavant) pour mettre un peu de bonne humeur. Deux amis, un physicien et un mathématicien vont voir une conférence sur la théorie des cordes.
Après un exposé extrêmement complexe à grands coups de repliements de variétés de Calabi-Yau dans des espaces de dimensions 11.... le physicien dit :
- Wow, c'était dur. Bon sang, tu arrives à te représenter ce genre de trucs à 11 dimensions ?
- Oui bien sûr.
- Mais comment fais-tu ???
- Je me les représente à N dimensions puis je pose N=11

[Adri0]

Bonjour à tous et merci pour vos messages/explications !!

Sethy

Si j’ai saisi ce que vous me dites, lors de la mesure de la valeur d’un qubit celui-ci se projette dans l’état mesuré. Ce qui détermine le centre de la sphère de Bloch suivante et ainsi de suite ce qui comme le souligne Deedee81 nous donne rapidement une représentation graphique imbuvable ou « incomplète » puisque je n’arrive pas à représenter correctement les différentes dimensions de chaque qubit. Un truc du style :

représentation graphique de 4 qubits(mesuré à chaque qubit).jpg
Mais dans le cas ou nous ne mesurons pas à chaque qubit ne pourrait il pas être représenté comme ceci :

4 qubits (ac 3 non mesurés).png

Dans cette représentation les 3 premiers qubits qui sont non mesuré et leurs états restent le vecteur représentant toutes les positions possibles de la superposition et le quatrième qubits qui lui est mesuré, ici représenté par un vecteur initié sur la troisième sphère et dont le point de « solution » est situé sur la quatrième sphère.

Etant donné,
« le cas Situation 1 + 2 n'est là que pour montrer que le point "solution" est bien le même dans les deux cas. »
Quelque soit « l’ordre » des qubits le point « solution » est le même, ne peut on pas mesurer l’état du quatrième dans une représentation de dimension 16 (si j’ai compris le principe) et en déduire un « vecteur optimal » pour chaque qubits précédant ?
(J’entend par « vecteur optimal » un vecteur qui n’aurai pas besoin de mesurer les états des qubits précédant ce qui « oblige » des calculs supplémentaires soit « une perte de temps »)
Ci-dessous en rose :
vecteur optimal.jpg

[Sethy]

Pièce jointe 445588

La sphère de Bloch a l'avantage de représenter tous les états possibles du qubit = a|0> + b|1>, avec a et b contraint par une seule relation a^2+b^2 = 1.

Ici, la représentation ne montre qu'un seul état bien précis pour les 4 qubits : a1|0000> + b1|0001> + c1|0010> + d1|0011> + ... + h1|0111> + ... + p1|1111>, alors que a peut prendre toutes les valeurs telles que a^2+b^2 = 1, que c peut prendre toutes les valeurs telles que c^2+d^2 = 1, e^2+f^2 = 1, ..., o^2 + p^2 = 1.

Il y a donc 8 paramètres indépendants (a, c, e, ....) et 8 dépendants (b, d, ...).

Mais dans le cas ou nous ne mesurons pas à chaque qubit ne pourrait il pas être représenté comme ceci :

Pièce jointe 445587

Dans cette représentation les 3 premiers qubits qui sont non mesuré et leurs états restent le vecteur représentant toutes les positions possibles de la superposition et le quatrième qubits qui lui est mesuré, ici représenté par un vecteur initié sur la troisième sphère et dont le point de « solution » est situé sur la quatrième sphère.

Cela revient simplement à fixer arbitrairement 7 des 8 paramètres indépendant et de ne laisser que "a" libre.

Ce qui revient exactement à ... la sphère de Bloch.

Pièce jointe 445586

Imaginons que tu connaisses la longueur (4m) d'un mur et sa hauteur (3m). C'est pratique puisque tu peux calculer sa surface.

Ce que tu fais avec ton schéma, c'est en quelque sorte "additionner" la hauteur et la longueur, ce qui te donne ici 7m. Comment déduire la surface d'un rectangle dont la somme de la longueur et de la hauteur donne 7m ? Est-ce 4x3 (=12), est-ce 5x2 (= 10), est-ce 7x1 (7) ?

Ici, dans ton schéma tu as représenté un objet à 16 dimensions avec un espace à 2. Tu as donc "perdu" 14 informations non seulement utile, mais indispensable.

[Adri0]

Merci pour les explications !!

« Ici, la représentation ne montre qu'un seul état bien précis pour les 4 qubits »
Oui je pensais représenter le vecteur des qubits mesurés.

«Ce que tu fais avec ton schéma, c'est en quelque sorte "additionner" la hauteur et la longueur»

Yep, je crois que je comprends ce que vous voulez dire, je n’ai pas réussi à représenter les 2 dimensions « supplémentaires » par qubit. Je ne sais pas si c’est possible d’ailleurs !?

[Adri0]

shéma dimensions 4 qubits ac code taille et couleurs2.jpg

1 qubit :

α ∙ |0› + β ∙ |1› = 1 objet à 2 dimensions soit 2 paramètres.

2 qubits :

α ∙ |00› + β ∙ |01› + γ ∙ |10› + δ ∙ |11› = 2 objets à 2 dimensions soit 4 paramètres ou 1 objet à 4 dimensions ?

3 qubits :

α ∙ |000› + β ∙ |001› + γ ∙ |010› + δ ∙ |011› + ε ∙ |100› + ζ ∙ |101› + η ∙ |110› + θ ∙ |111› = 4 objets à 2 dimensions soit 8 paramètres ou 1 objet à 8 dimensions ?

4 qubits :

α ∙ |0000› + β ∙ |0001› + γ ∙ |0010› + δ ∙ |0011› + ε ∙ |0100› + ζ ∙ |0101› + η ∙ |0110› + θ ∙ |0111› + ι ∙ |1000› + κ ∙ |1001› + λ ∙ |1010› + μ ∙ |1011› + ν ∙ |1100› + ξ ∙ |1101› + ο ∙ |1110› + π ∙ |1111› = 8 objets à 2 dimensions soit 16 paramètres ou 1 objet à 16 dimensions ?

Peu-t-on le noter ainsi :
« 8 objets à 2 dimensions soit 16 paramètres ou 1 objet à 16 dimensions. »
Avec la condition stricte admettant chaque objet dans un espace différent.
Ou est-ce une aberration ?

[Sethy]

Si tu veux bien, refait le premier dessin avec seulement 2 qubits.

Mais dessine une 30aine de valeurs possibles pour le premier qubit (dans l'espace, donc avec aussi des vecteurs qui viennent vers toi et qui au contraire s'éloignent de toi, en diagonale, essaie d'occuper toute la surface du globe). Ensuite, au départ de ces 30 valeurs là pour le premier qubit, dessine la sphère de Bloch du second qubits.

[Adri0]

j'ai mis le premier qubit en rouge

[Adri0]

de ce que je comprend, le premier qubit a pour état toutes les positions possibles représenté par une sphère de Bloch. Ce qui "positionne" le deuxième qubits avec pour centre un point de cette première sphère. mais c'est le cas pour un premier qubit non mesuré ? si il est mesuré nous connaissons un état de un seul vecteur?

[Sethy]

Pièce jointe 445676

j'ai mis le premier qubit en rouge

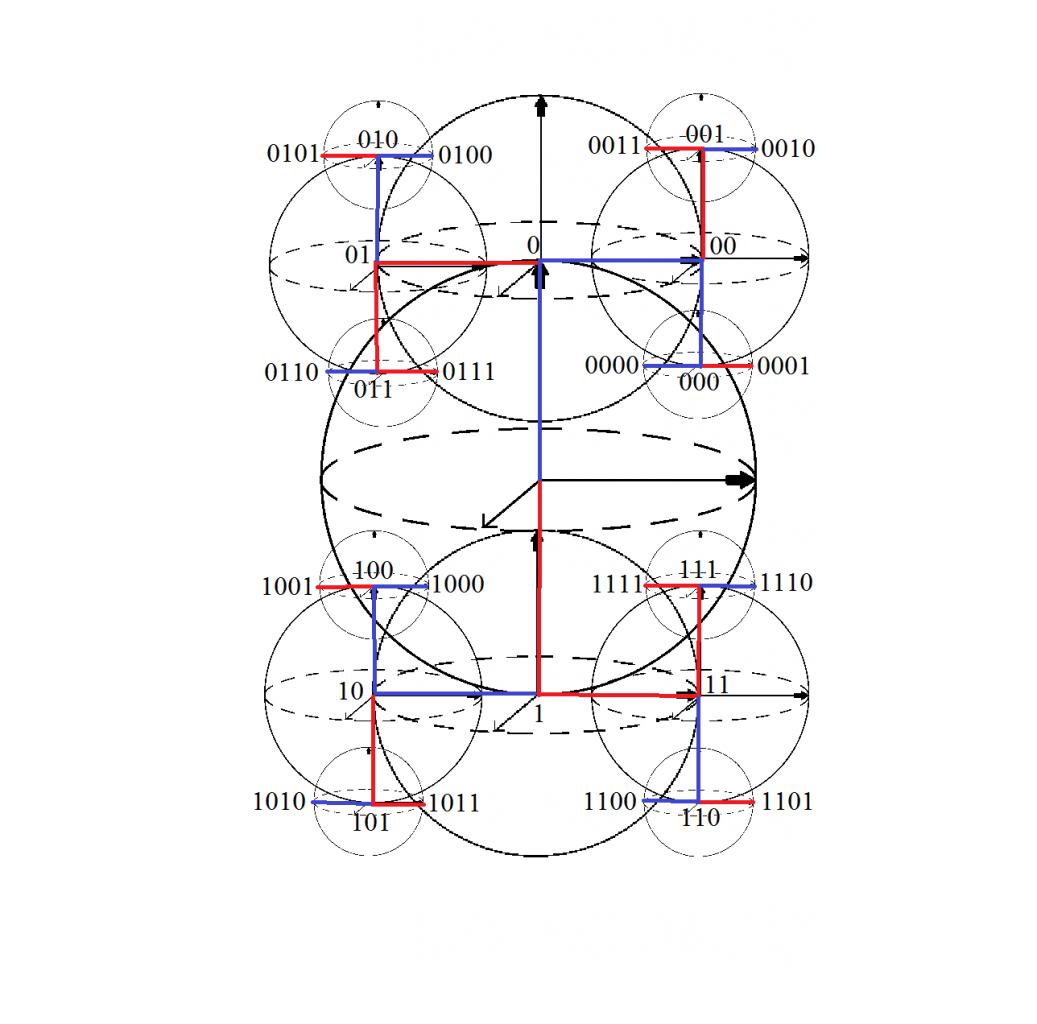
Pour que la représentation ait un sens, il faut je le rappelle qu'un point de l'espace ne corresponde qu'à une et une seule valeur pour tous les qubits.

Ici regarde combien il y a de points d'intersections. Ce sont autant de situations équivoques, hors la représentation qui est recherchée doit être univoque (bijective).

Si tu veux tu peut refaire la même opération avec 30 positions pour chacun des qubit secondaires. Et évidemment aux 900 positions obtenues, tu ajoutes un sphère de Bloch ...

Pour répondre à la question du post suivant, à quoi sert de ne mesurer qu'un seul qubit dans un ensemble ? Si tu veux mesurer un seul qubit, tu n'en crées qu'un seul et puis c'est tout. A quoi sert de ne représenter qu'un seul qubit dans un ensemble puisque c'est ce que tu fais. Prend n'importe lequel de tes graphes et ajoute à chaque fois 30 positions par qubits : 30 ... 900 ... 27000 ... 2430000 sphères de bloch pour le 4ème qubits. Et ça, ce n'est rien qu'avec 30 positions, imagine avec une infinité ...

[Deedee81]

Salut,

Les tentatives de représentation ci-dessus illustrent bien ce que je disais. Dès qu'on a plusieurs q-bits, les représentations deviennent imbuvables et inutiles.

de ce que je comprend, le premier qubit a pour état toutes les positions possibles représenté par une sphère de Bloch. Ce qui "positionne" le deuxième qubits avec pour centre un point de cette première sphère. mais c'est le cas pour un premier qubit non mesuré ? si il est mesuré nous connaissons un état de un seul vecteur?

Quand je lis ça il me semble comprendre ta difficulté. Tu penses comme si ce deuxième q-bit était indépendant de la valeur du premier (puisque tu dis "centrer la deuxième sphère sur le point du premier vecteur"). Mai!s c'est faux. Il est vrai que c'est une propriété non classique (et absolument sans équivalent classique).

Prenons un exemple simple. Soit un seul objet, pour illustrer prenons le chat de Schrödinger et appelons-le Minet. Il peut être mort, vivant, ou à la fois mort et vivant (pour faire simple car il peut y avoir pleins de pondérations possibles).

On pourrait représenter ça par trois cas "M", "V" ou "VM".

Prenons un autre chat, Sylvestre. On peut lui aussi représenter ça par "M", "V", "VM".

Pour les distinguer mettons l'initiale de leur nom :"Mm", "Vm" ou "VMm" et "Ms", "Vs" ou "VMs".

Supposons que le premier soit "VMm", on pourrait alors mettre les possibilités du deuxième à coté :
"VMm" <-> "M", "V" ou "VM".
C'est l'équivalent de ce que tu proposais avec les sphères.

Oui mais il y a aussi des états comme :
"Mm" <-> "Vs" et "Vm" <-> "VMs" (c'est pas deux états avec un ou mais bien un seul état)
par exemple
Et toutes les autres possibilités. Comment les représenter sans perte d'information, par exemple si on dessine
"Mm" <-> "Ms"
"Vm" <-> "Vs"
alors c'est incomplet car ça pourrait être "Mm" <-> "Ms" ou "Vm" <-> "Vs" ou encore "Mm" <-> "Ms" et "Vm" <-> "Vs".

Seule possibilité donner la liste complète de toutes les possibilités. Et à on est mal car ce n'est plus un dessin (même si on met de jolies couleurs, de jolies boules...) c'est juste une liste, une énumération.

Et si en plus on ajoute les pondérations "x"+"y" ou "x"+2"y" ou "x"+1,3"y" ou "x"+i "y" ou "x"+(1+2i)"y" (je n'ai pas normalisé mais ça change peu de chose) alors il faudrait un "dessin" (= énumération) inifni.

Pourquoi cette difficulté ? Par ce que avec un dessin fait sur une feuille de papier on ne sait que représenter des choses classiques (on pourrait même en fait un modèle en pâte à modeler). Or la superposition quantique n'a aucun équivalent classique et ne peut pas en avoir (c'est même un théorème : celui de Bell, vérifie expérimentalement par Aspect pour la première fois).

Donc, on est totalement démuni : il est impossible d'avoir une représentation graphique valable de deux qbits, seule les maths permettent de s'en sortir (et on peut "dessiner" les formules, mais c'est certainement par ce qui est recherché ici, l'interprétation du dessin n'étant plus classique).

[Deedee81]

Donc, on est totalement démuni : il est impossible d'avoir une représentation graphique valable de deux qbits, seule les maths permettent de s'en sortir (et on peut "dessiner" les formules, mais c'est certainement par ce qui est recherché ici, l'interprétation du dessin n'étant plus classique).

Ou pour le dire autrement, les états de deux q-bits sont infiniment plus riches que toute représentation classique de deux q-bits. Ici "infini" est à prendre au sens littéral ! Ce qui empêche toute représentation.

Ce n'est pas pour rien que les calculateurs quantiques (quant ils seront vraiment opérationnels) sont beaucoup plus puissants que les ordinateurs classiques (même si in fine on perd l'infinité des valeurs possibles à cause de la mesure et de quelques trucs associés comme l'impossibilité de cloner un état quantique, ce qui oblige à ruser pour que l'essentiel du calcul se fasse au niveau quantique avant mesure, la programmation d'un calcul quantique est un vrai cauchemar mais on commence à voir des techniques de programmation, des librairies, etc....). C'est ça qui permet de calculer un problème NP-complet en temps polynomial (comme la factorisation des grands nombres) ou d'accélérer (fortement) la recherche en base de données. Si on pouvait représenter par un graphique classique les états quantiques de plusieurs q-bits alors on pourrait construire l'équivalent avec un calculateur classique (qui programmerait la représentation et l'utiliserait) et .... on pourrait se passer des calculateurs quantiques. Mais ce n'est pas le cas malheureusement (sinon on ne se gênerait pas pour le faire).

EDIT a contrario, représenter un seul q-bit est possible (la sphère de Bloch) car on a aussi une infinité classique : le continu (des réels ou d'une courbe ou de la surface d'une sphère).
Et de fait bien qu'ayant un comportement classique un seul q-bit ne permet pas de faire de calcul quantique plus rapide qu'un calcul classique.

[Adri0]

Bonjour,
Merci pour vos réponses !!

J’ai en effet du mal à comprendre cette notion « d’infinité » de superpositions possibles…(et le fonctionnement de la physique quantique en général probablement)
Peu t on définir α ∙ |0› + β ∙ |1› comme un ensemble fini ? Avec une multitude de positions possibles ? c’est alors plus commode de parler d’infinité (A prendre comme vous le dites au sens littéral de ce fait).
Dans mes représentations avec des sphères de Bloch, j’ai (essayé) de représenter une superposition de qubits mesurés, avec la réinitialisation engendrée par la mesure il me semblai « logique » de « centrer la deuxième sphère sur le point du premier vecteur » et de « perdre » les autres informations au passage. N’est ce pas ce qu’il ce passe lors d’une mesure ?

α ∙ |0› + β ∙ |1› lors du premier qubit

si non mesuré, deux qubits : α ∙ |00› + β ∙ |01› + γ ∙ |10› + δ ∙ |11› dans ce cas nous avons un objet dans un espace à 4 dimensions.

si mesuré, nous « perdons » des informations et nous réinitialisons un autre qubit α ∙ |0› + β ∙ |1› à partir de la position mesurée du premier qubit mais dans un espace différent , dans ce cas nous avons 2 objets chacun dans un espace à 2 dimensions.

Le deuxième cas est porteur de beaucoup moins d’informations que le premier et en même temps représente une des positions possibles.

Peu t on alors écrire :
α ∙ |00› + β ∙ |01› + γ ∙ |10› + δ ∙ |11 ≥ [α ∙ |0› + β ∙ |1›] + [ α ∙ |0› + β ∙ |1› ]
(code couleurs pour représenter qu’il s’agit de deux qubits dans des dimensions différentes, pour ne pas tomber dans le piège de « l’addition hauteur + longueur »).


Concernant la perte d’information lors d’une mesure, est ce que cela peu être imputé au système booleen qui admet 1 = true et 0 = false ? parce qu’ au final que ce soit des bits ou des qubits, nous admettons un résultat binaire. (D’où la dernière représentation partagé dans le message 26).

Un truc du style :
Si 101 est la « bonne » position

Avec une mesure au troisième qubit :

Pour ζ ∙ |101› = true (1 en réponse binaire)
alors
α ∙ |000› + β ∙ |001› + γ ∙ |010› + δ ∙ |011› + ε ∙ |100› + η ∙ |110› + θ ∙ |111 = false (0 en réponse binaire)


Avec mesure à chaque qubit :
En bleu les informations qui seront perdu après la mesure

α ∙ |0› + β ∙ |1› l’état du premier qubit est transporté sur le deuxième. l’information : 1 considéré comme vrai est conservé à laquelle est appliqué le second qubit α ∙ |0› + β ∙ |1› pour obtenir une information du type 10 ou/et 11.

α ∙ |0› + β ∙ |1› L’état du deuxième qubit est transporté sur le troisième. L’information : 0 considéré comme vrai est conservé à laquelle est appliqué le troisième qubit α ∙ |0› + β ∙ |1›
pour obtenir une information du type 100 et/ou 101 (étant donné les deux informations 1 et 0 conservées au préalable)


Soit une « perte » substantiel d’informations importantes à chaque nouvelle mesure :
α ∙ |0› + β ∙ |1›
α ∙ |00› + β ∙ |01› + γ ∙ |10› + δ ∙ |11›
α ∙ |000› + β ∙ |001› + γ ∙ |010› + δ ∙ |011› + ε ∙ |100› + ζ ∙ |101› + η ∙ |110› + θ ∙ |111›
mais puisque que les informations « perdues » sont déterminées fausses au moment de la mesure, pourquoi continuer à « creuser dans ce sens là » ? (dans le cas présenté si 101 est la « bonne » réponse pas besoin de calculer toutes les informations qui découle de 0 après le premier qubit)

Pour conserver toutes les informations est il possible d’avoir
1 = true et 0 = false ET 1 = false et 0 = true.

101 = true
si
[000 et 001 et 010 et 011 et 100 et 110 et 111 = false] est true


L’absence d’information est une information en soit.
(la phrase m’est venu comme ça probablement nimp mais bon après mon scmilblick sur la perte d’information lors d’une mesure je suis plus à ça près lol)

En tt cas encore merci pour vos explications !