Bonjour , j’aurai besoin d’un petit éclaircissement pour la dernière question.
Un bloc de masse m = 12 kg est maintenu contre un ressort sans lui être attaché. Le ressort
de masse négligeable et de constante de rappel k = 120 N/m est comprimé de x = 2 cm. comme illustré sur la figure ci-dessous. Lorsqu'on lâche le ressort, le bloc part du repos et glisse sur un plan AB inclinée de © = 30° par rapport à l'horizontale. Le bloc parcourt ensuite une surface BC de longueur 10 m et une rampe circulaire de rayon R. Les surfaces AB et BC sont rugueuses avec un coefficient de frottement cinétique Uc= 0,15 et les
autres surfaces sont considérées lisses. On suppose que le bloc reste en contact avec la surface tout au long de son trajet.
a) En utilisant la variation de l'énergie mécanique, trouver le module de la vitesse du bloc au point B.
b) En utilisant le théorème de l'énergie cinétique, trouver le module de la vitesse du
bloc au point C.
c) En utilisant la deuxième loi de Newton et la variation de l'énergie mécanique.montrer que la norme de la force de réaction de la rampe circulaire en E s'exprime par
N=m[ VD^2/R + 3gcosa]
d) En déduire le module de la vitesse minimale au point D , VD-min pour que le bloc reste en
contact avec la rampe circulaire au point F, soit le point le plus haut de la rampe circulaire
Normalement pour la d) il faudrait qu’à ce point la réaction du support ne soit pas nulle a l’instant où il arrive au point F donc il faudrait que
N=m[ VD^2/R + 3gcosa] ou a =180 degré soit nulle n’est-ce pas ?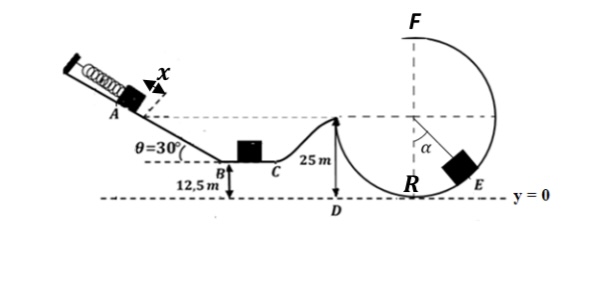
-----




