Déterminer un solénoïde long

[Martin0019]

Bonjour à tous/toutes,

J'aimerai pouvoir qualifier un solénoïde comme étant long en fonction du nombre de spires qu'il a.
Là où je bloque, c'est que la seule formule que j'ai (||B|| = µ*n*I) me permette de calculer le champ magnétique d'un solénoïde long, mais pas de pouvoir trouver une fonction f(N)=B (N étant le nombre de spires et B le champ magnétique généré), qui pourrait me permettre de montrer une évolution asymptotique du champ, et dont je pourrai ensuite estimer à partir de combien de spires le champ magnétique ne dépend plus du nombre de spires.

En fait, je n'arrive pas à mettre sur feuille le fait que le champ magnétique dépend du nombre de spires jusqu'à un certain nombre.



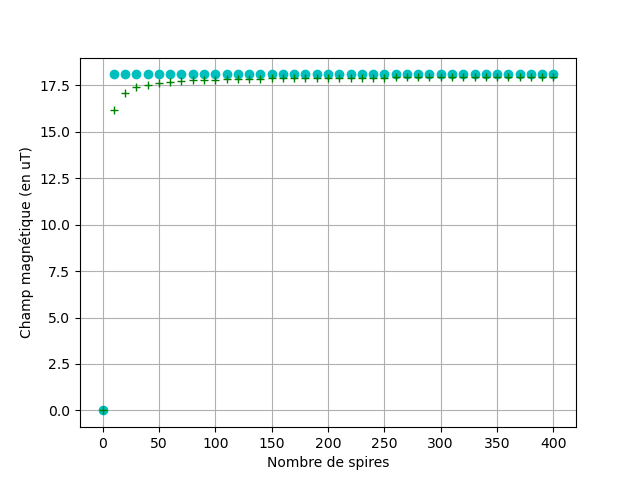
J'ai mit ci-dessus un graph que j'ai fait sur python avec en point bleu ce que j'ai et en croix vertes le modèle de la courbe que j'aimerai avoir.

Si vous le voulez, voici le code python que j'ai fait pour faire ce graph:

import numpy as np
import matplotlib.pyplot as plt

#B : champ magnétique en T
#mu : perméabilité magnétique en T m/A. T
#N : nombre de spires 
#I : Intensité en A
#L : longueur du solénoide en cm

I=3 #Ampere



mu = 4*np.pi*(10**(-7)) #T m/A. T
#En supposant que le n=(nombre de spires/cm) = 4,8 cm**-1
#n=N/L

N=[i for i in range(0,410,10)]
L=[N[i]/4.8 for i in range(len(N))]
#L=40*(10**(-2))

def f(N,L):
    B=[0]
    for i in range(1,len(N)):
        champ=(mu*I*N[i])/L[i]
        B.append(champ)
    return B

B_uT=[i*10**6 for i in f(N,L)]


def g(N):
    asymptote=[0]
    for i in range(1,len(N)):
        asymptote.append(19-((N[i]+18)/N[i]))
    return asymptote

plt.figure()
plt.plot(np.array(N),np.array(B_uT),'co',label='Pour un solénoïde long')
plt.plot(np.array(N),np.array(g(N)),'+g',label="Modèle que j'aimerai trouver")
plt.xlabel('Nombre de spires')
plt.ylabel('Champ magnétique (en uT)')
plt.grid() 
plt.show()

Auriez-vous un conseil à me donner pour que je puisse trouver une relation entre B et N ?

Merci d'avance,
Martin
-----

[gts2]

Bonjour,

Vous voulez le champ où ? Au centre, sur le bord, sur l'axe ou pas ...

Sur l'axe, voir par ex. wikipedia (première réponse de Gxxx à "solénoïde")

Sinon pour ce qui est de la dépendance vis à vis de N, vous l'avez puisque n=N/L.

[Martin0019]

Bonsoir,

En lisant la page que vous m'avez envoyé, je me suis rendu compte que mon raisonnement était en effet faussé.

De plus, la détermination du champ magnétique sur l'axe (cf https://fr.wikipedia.org/wiki/Sol%C3%A9no%C3%AFde ) me permettrait de dire si la bobine est longue ou non (si la variation maximale de champ sur toute sa longueur, donc a priori entre le centre et les bords longitudinaux, qu'on pourrait noter Bmax - Bmin, est compatible avec l'hypothèse d'uniformité (c'est-à-dire une valeur de référence égale à 0)).

Cependant j'ai encore quelques questions:
- Comment trouve-t-on cette formule ? Faut-il l'admettre ?

Le champ magnétique créé par une spire de courant sur son axe : B(x)=μ0 * i *sin(θ)³/2R

- Serait-il possible de me donner les infos que vous avez, un conseil, ou une méthode à adopter pour pouvoir trouver ces formules de trigonométrie dont parle la page ? (C'est quelques lignes en dessous du début de la page)



Merci d'avance,
martin

[gts2]

Pour ce qui est du champ créé par une spire, tout dépend de votre niveau d'étude, soit vous l'admettez, soit voir par ex. : lappweb.in2p3.fr p. 62 sqq

Pour la trigo, je ne comprend pas trop la question : s'il s'agit des expressions des cos \theta1 et 2, c'est la définition usuelle adjacent/hypoténuse

[A voir en vidéo sur Futura]

[Martin0019]

Bonjour,

Merci pour la rapidité et la pertinence de vos réponses, qui m'ont été d'une grande utilité.
(et pour les cosinus je n'avais pas fait le rapprochement avec adj/hyp , j'espère que c'était dû à la fatigue.........)

Bien à vous,
Martin