En I le rayon issue de M2 coupe M1
-----

En I le rayon issue de M2 coupe M1

Jai une idée : La droite LI participe à la différence de marche...

Désolé, je n'avais pas vu qu'on était passé à la page 2.
(réponse au message 1) Non, ça c'est le rayon incident. Il vient d'en haut à gauche, passe par I et arrive sur M2 en J.
Donc, par où passe le rayon qui revient de M2 vers M1 ?
Dernière modification par Sethy ; 01/10/2022 à 22h17.
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.

Par la droite IJ...
C'est vrai qu'il n'y a pas les flèches des rayons.

Le rayon arrive par la droite IJ, donc à moins d'être perpendiculaire au miroir, il ne peut pas repartir par IJ (où alors tu as des drôles de miroirs chez toi).
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.

Peux tu me dessiner le déphasage car je me perds.

Si le rayon incident IJ touche le miroir en M2, par où va-t-il après ?
Code:I \....|m2 .\...|m2 ..\..|m2 ...\.|m2 ....\|J .....|m2 .....|m2 .....|m2 .....|m2
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.

Il fait un angle i avec l'horizon d'après Descartes
Une autre tentative : IJ/e=cosi d'après la loi de la réflexions sur un miroir plan...
Dernière modification par lesurveilleur ; 01/10/2022 à 22h28.

Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.

Il fait un angle i avec l'horizon d'après Descartes
Une autre tentative : IJ/e=cosi d'après la loi de la réflexions sur un miroir plan...

Le rayon IJ qui se réfléchi sur le miroir en J par où est-il réfléchi : a,b,c,d,e,f,g,h ou k.Code:I \....|m2 a\...|m2 b.\..|m2 c..\.|m2 d...\|J e....|m2 f....|m2 g....|m2 h....|m2 k
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.

h car i=i'

OK, parfait !
Sur le schéma original, à quelle lettre correspond h (sur le schéma de l'expérience) ?
Donc quelle est la distance totale parcourue ? On sait qu'entre I et J, c'est IJ mais entre J et ... c'est combien ?
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.

Entre J et I c'est IJ également

Ca, c'est le trajet "aller". Il y a un trajet retour. Tu viens de le trouver.
Donc, sur le schéma de l'expérience à quoi cela correspond-il ?
Pièce jointe 467408
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.

Il s'agit de JK...

OK ... et maintenant IJ+JK ... avec les relation trigonométrique cela donne ...
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.

En prenant la bissectrice de IJK i=il on obtient 2 cos i * e

Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.

Je vois pas quelle relation trigo utiliser.... Peut être
AL KHASHI car on est pas dans un angle droit...

Tu ne cherchais pas 2 * e* cos(i) ? C'est ce que tu viens de trouver.
Mais comme je le disais, il faut aller voir du côté du théorème de Malus ainsi que de la physique de l'expérience de Michelson.
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.

Dernière question un peu cadide à quoi sert le LK mis en avant sur la figure ? D'habitude il s'agit de la différence de marche...

C'est là qu'intervient la physique. Il faut trouver l'angle i tel que les ondes soient en phase. Et pour cela il faut (je pense) appliquer 2x le théorème de Malus une fois en L et une fois en K. (Ici, attention, je suis prof de chimie à la base et pas physicien).
Tout est toujours plus complexe qu'on (que je) ne le pense de prime abord.

Je ne vois pas trop d'où sort votre "d'habitude".
Le principe est de découper la différence de marche en petits morceaux avec un morceau nul obtenu par le théorème de Malus.
Dans le cas présent, on place une source au point d'observation M à l'infini qui envoie des rayons parallèles et donc, comme vous le dites, "le front d'onde est perpendiculaire au rayon", on trace donc LK perpendiculaire aux rayons et Malus me dit que (ML)=(MK).
Ensuite on découpe : (SM)2-(SM)1=((SI)+(IJ)+(JK)+(KM)) - ((SI)+(IL)+(LM)), on simplifie et on trouve (SM)2-(SM)1=(IJ)+(JK)-(IL)
Ceci étant pour le Michelson, on peut faire plus simple, vous vous êtes déjà débarrassé de la séparatrice, vous pouvez faire de même en vous débarrassant des miroirs en utilisant l'image de la source par ceux-ci S'1 et S'2.
Cela donne (SM)2-(SM)1=((SS'1)+(S'1M)) - ((SS'2)+(S'2H)+(HM))=(S'2H)=2e cos(i) directement, puisque pour un miroir plan (SS')=0.
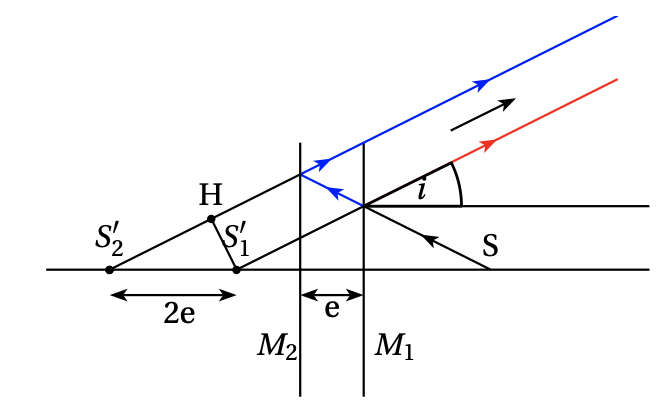

Peux tu mettre les indices des miroirs ? M1 ET M2...


Dans tes calculs de chemin optique

(SM)2 signifie chemin de S à M en passant par le miroir 2 : le 2 est donc bien présent, les points du chemin 2 IJK sont ceux du dessin
(SM)1 signifie chemin de S à M en passant par le miroir 1 : le 1 est donc bien présent, les points du chemin 1 IL sont ceux du dessin
Pour l'autre, je réécris car j'ai fait des interversions
(SM)2-(SM)1=((SS'2)+(S'2H)+(HM)) - ((SS'1)+(S'1M))=(S'2H)=2e cos(i)
(SM)2 signifie chemin de S à M en passant par le miroir 2 ...

