Propagation fluide

[tpscience]

Bonjour à tous,

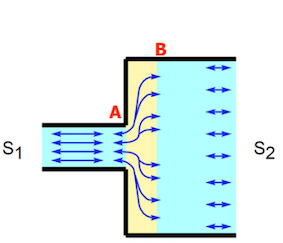
J'étudie le cas de la propagation d'une onde sonore entre 2 milieux séparés par une interface en x=0. Les caractéristiques sont , et (surface, masse volumique et célérité) pour le milieu 1 et respectivement pour le milieu 2 (et ). Les ondes incidente, réfléchie et transmise sont définies comme :





Je cherche une relation entre , et .

Je pensais partir du PFD comme : , et de la condition de continuité des pressions (grandeur locale) : . Mais comment combiner les deux pour obtenir une relation finale entre , et ?

Merci
-----

[gts2]

Bonjour,

Pi+Pr=Pt est le PFD comme S1 Pi + S1 Pr = S2 Pt (avec un +)
Il faut donc choisir entre les deux et pour cela modéliser l'écoulement au niveau du changement de section : on prend la continuité de la pression.

Une onde se décrit par deux variables, quelle est l'autre variable dans ce cas ? Quelle loi générale peut-on écrire sur celle-ci ?

[tpscience]

Bonjour, le moins venait du fait que l'onde réfléchie allait dans le sens des x décroissants.
Qu'entendez-vous par autre variable ? Ici, le problème évolue suivant des coordonnées spatiales et temporelle, et les fonctions qui nous intéressent sont la vitesse et la (sur)pression.

[gts2]

Bonjour, le moins venait du fait que l'onde réfléchie allait dans le sens des x décroissants.

Moi je veux bien (en fait non !), mais alors il faut être cohérent et écrire Pi-Pr=Pt !

Qu'entendez-vous par autre variable ? Ici, le problème évolue suivant des coordonnées spatiales et temporelle, et les fonctions qui nous intéressent sont la vitesse et la (sur)pression.

C'est cela : l'autre variable (j'aurai du dire grandeur) est la vitesse, quelle loi générale peut-on écrire en faisant intervenir la section ?

[A voir en vidéo sur Futura]

[tpscience]

La conservation du débit.

[gts2]

C'est bien cela.
Vous avez maintenant deux équations et six inconnues et vous cherchez un rapport, il vous faut donc trois autres relations reliant P et u.

[tpscience]

Pi+Pr=Pt est le PFD

C'est-à-dire ? Cela n'est vrai que dans le cas d'une section identique, et donc d'une simplification du problème. Mais plus généralement cela découle de la conservation du débit volumique à l'interface, non ?

[gts2]

La conservation du débit c'est vi+vr=vt (à section constante), ou plus généralement Di+Dr=Dt avec D=vS

Si on prend la surface de séparation (surface donc masse nulle), le PFD donne ma=somme des forces=0, soit pour une section S (Pi+Pr)S=Pt S donc Pi+Pr=Pt.

Votre équation (Pi+Pr)S1=Pt S2 est donc bien la même chose, mais quel est le système auquel vous appliquez les forces ? En supposant par exemple S2<S1, (Pi+Pr)(S1-S2) s'applique sur la paroi.

"donc d'une simplification du problème", c'est bien ce que j'ai dit au début "pour cela modéliser l'écoulement au niveau du changement de section"

[tpscience]

Il a une section S2<S1, donc j'arrive au changement de section :



avec la pression du fluide à l'interface.

[gts2]

Quelle distinction faites-vous entre pression du fluide Pf et Pi, Pr : Pf=Pi+Pr, non ?

[tpscience]

Ok, donc on arrive à Pi+Pr=Pt.

Nous n'avons donc pas besoin de l'équation de continuité à l'interface sur la surpression pour obtenir cette relation à partir du PFD ?

[gts2]

Je ne comprends pas trop : le PFD donne P1=P2 qui est justement l'équation de continuité.

Sinon, pour revenir à la modélisation, cela ressemble à qqch du genre :



On écrit la conservation du débit entre A(1) et B
On écrit la continuité de la pression en A

Puis on suppose que le gaz s'étale suffisamment rapidement pour que P(B,2)=P(A,2), autrement dit il faut que la zone de transition soit faible par rapport à la longueur d'onde.