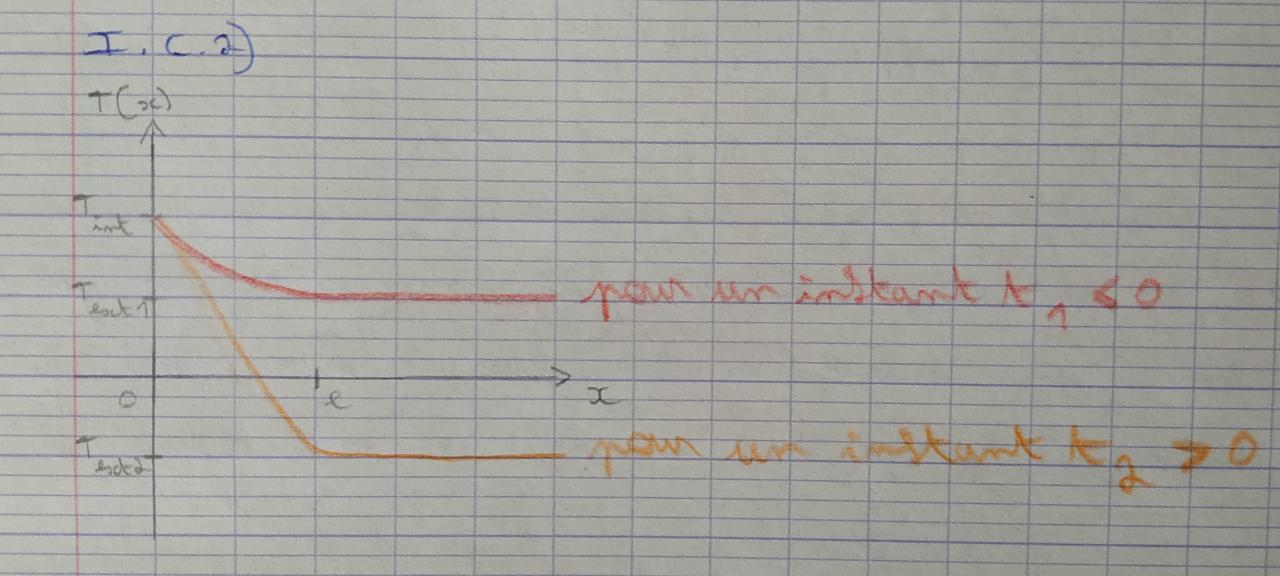Résolution de l'équadiff de transport de chaleur

[Matt1627]

Bonsoir, j'ai l'équadiff suivante à résoudre: ρ*C *(dT/dt) = λ*(d²T/dx²). Comment faut-il s'y prendre pour la résoudre ? car je n'ai jamais résolu une équation avec une dérivée temporelle et une spatiale. On me parle de conditions initiales et de conditions aux limites. Pourriez-vous me donner la marche à suivre svp ? A moins que le fait que ce soit précisé en régime permanent m'indique que la dérivée temporelle est nulle ?

Merci d'avance à toute personne m'accordant un peu de son temps.
.
-----

[gts2]

Bonjour,

Si vous donniez l'énoncé exact ...

Parce que la donnée de conditions initiales n'est pas très cohérente avec l'hypothèse régime permanent (qui peut signifier, en effet, dérivée temporelle nulle).

[Matt1627]

Euh à vrai dire je me suis mal exprimé, il n'y a que des conditions aux limites mais je dois la résoudre pour 2 instants particuliers différents. L'énoncé est:

Résoudre cette équation en régime permanent, avec les conditions aux limites de types températures imposées trouvées à la question précédente:
- pour un instant particulier négatif t₁<0,
- pour un instant particulier positif t₂>0, très longtemps après la variation de température extérieure, quand le régime permanent est de nouveau établi dans le mur.

[gts2]

A lire entre les lignes, parce que comme énoncé exact ...

On va dire qu'en effet la dérivé temporelle est nulle.

[A voir en vidéo sur Futura]

[Matt1627]

Numérisation_20221228.jpg
Numérisation_20221228 (2).jpg

Voici l'énoncé exact pour être sur qu'il n'y ait aucune info importante manquante. C'est la question I.C.1)
Mais du coup l'équation à résoudre est juste: λ*(d²T/dx²) = 0 ?

[gts2]

C'est bien cela.

[Matt1627]

D'accord, je vous remercie car sinon si il n'y avait pas le fait que ce soit en régime permanent, l'équation de départ aurait-elle été facilement résolvable ?

[gts2]

Les équations aux dérivées partielles sont rarement "facilement résolvable".

[Matt1627]

D'accord donc pour résoudre une telle équation, il faut forcément une hypothèse pour simplifier un terme de dérivé ?

[gts2]

Il peut exister des solutions mais pas forcément simples. Dans votre cas on obtient, par exemple, (en adimensionné), yaplusk trouver k, Ak, \phik ...

[Matt1627]

Là du coup, j'essaie de résoudre l'équation, pour moi T est donc de la forme A*x + B avec A et B des constantes. Mais j'ai l'impression que mes conditions aux limites sont fausses ou que ce ne sont pas celles attendues car j'ai dit que dT(0,t)/dt=dT(e,t)/dt=0 pour la I.B.1)(i) et pour la (ii) j'ai dit que T(0,t)>=T(e,t). Qu'en pensez-vous ? Peuvent-elles me permettre de poursuivre car j'en ai pas l'impression? De plus, je n'ai pas compris quelle va être la différence entre les 2 instants où je dois la résoudre.

Merci d'avance pour votre aide.

[gts2]

Là du coup, j'essaie de résoudre l'équation, pour moi T est donc de la forme A*x + B avec A et B des constantes.

C'est bien cela.

mes conditions aux limites sont fausses ou que ce ne sont pas celles attendues car j'ai dit que dT(0,t)/dt=dT(e,t)/dt=0

Vous en avez déjà tenu compte (stationnaire). Mais vous connaissez les températures en x=0 et x=e.

mes conditions aux limites sont fausses ou que ce ne sont pas celles attendues car j'ai dit que T(0,t)>=T(e,t).

C'est bien cela et vous connaissez T(0,t)=Text et T(e,t)=Tint

De plus, je n'ai pas compris quelle va être la différence entre les 2 instants où je dois la résoudre.

Text n'est pas la même

[Matt1627]

D'accord, merci pour votre réponse. Pour la question I.C.3), qu'est ce qui est attendu ? car je ne vois pas ce que je peux rajouter à ce que j'ai fait à la question précédente.

[gts2]

T=a*x+b est une droite, ce qui n'est pas vraiment le cas sur votre graphe, prenez une règle éventuellement.

Pour ce qui est de I.C.3 il faut représenter le passage de l'un à l'autre, donc une série de courbe s'étalant de t=0+ à t= quelques tau (tau : temps caractéristique)

[Matt1627]

D'accord, merci à vous.