Bonjour à tous,
Je suis cycliste et dans ma pratique je suis venu à me poser une question physique à laquelle j'ai dû mal à trouver une réponse, mes lointains cours de MP ne m'étant guère utiles.
Dans le cyclisme moderne, on évalue la qualité physique d'un coureur par la puissance en watts qu'il peut développer pendant un certain temps (disons 5 min ici, c'est à dire la PMA pour Puissance Maximale Aérobie). Cette donnée brute est souvent mise en relation avec la masse du coureur pour avoir une meilleure idée des capacités du coureur lorsque la pente se raidit. Cela se fait en divisant la PMA (en watts) par la masse, ce qui donne donc une PMA en w/kg. Un cycliste de 80kg avec une PMA de 400W a donc une PMA de 5W/kg ; un autre de 60kg avec une PMA de 300W a aussi une PMA de 5W/kg. Sur le plat ou sur une pente très faible le coureur le plus lourd aura l'avantage, mais plus la pente s'élève, plus l'avantage passe au coureur le plus léger.
La question qui m'est venue est donc à partir de quelle pente, le rapport de force s'équilibre.
Armé de mes maigres souvenirs de ma mécanique de prépa, j'ai décidé de poser l'inusable PFD à mon cycliste en m'attendant à trouver assez facilement une solution pour la pente limite, en fonction des masses des deux coureurs comparés, car je suppose que la différence de masse a une influence sur la pente limite. En vous passant mes douloureuses retrouvailles avec les coordonnées cartésiennes, j'ai abouti à ceci, en appliquant le PFD à un cycliste à vitesse constante sur une pente d'angle α et en ne prenant en compte que le poids, donc en négligeant principalement la résistance de l'air et les frottements sur la route :
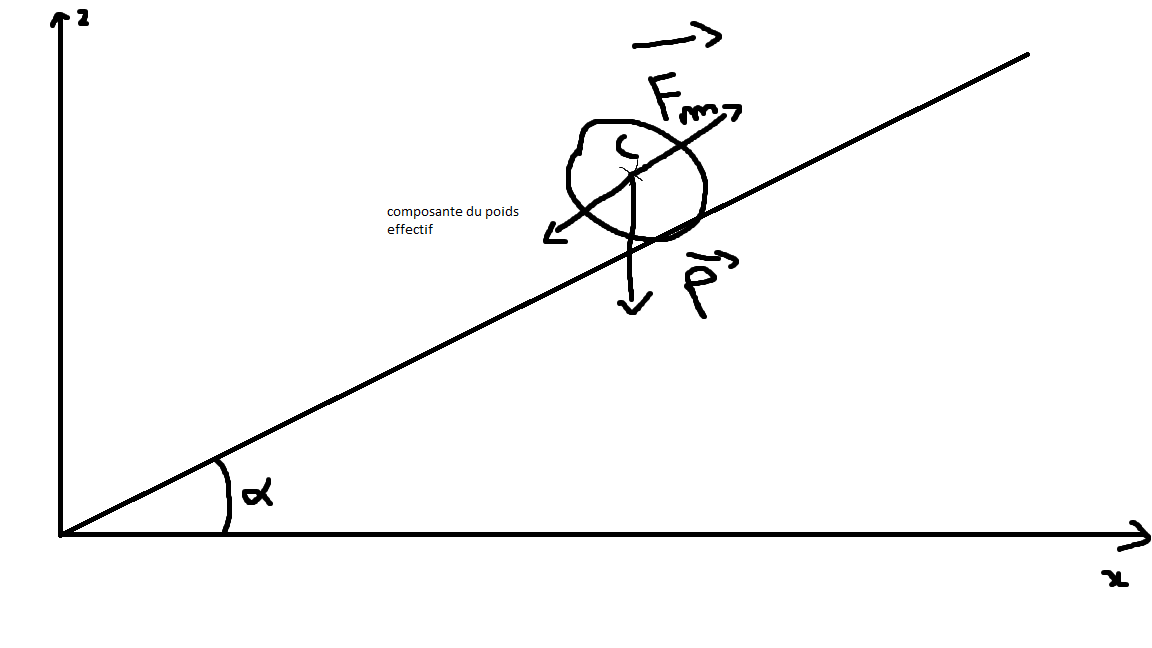
ma=∑F or a=0 car vitesse constante et ∑F=Fm (Force musculaire pour avancer) + p(poids = m*g*sin(α)) (ce sont des vecteurs mais je ne sais pas comment l'écrire)
=>Fm = m*g*sin(α) (en norme)
Or Fm = puissance du cycliste(W) / vitesse(V) => W/V = m*g*sin(α) => W/m = V*g*sin(α) et pour plus tard V=W/(m*g*sin(α))
Ici, pour nos deux coureurs C1 (masse=m1 et PMA=w1) et C2 (masse=m2 et PMA=w2), si ils ont la même PMA en W/kg => w1/m1 = w2/m2
On recherche donc l'angle limite α pour lequel lorsque nos deux coureurs sont à PMA, ils roulent exactement à la même vitesse.
Soit α tel que : v1=v2 [vitesse des deux coureurs égale] => W1/(m1*g*sin(α)) = W2/(m2*g*sin(α)) or comme w1/m1=w2/m2 tout se simplifie !! Et là je ne comprends pas !
Négliger la résistances de l'air aboutie à des résultats complètement faux mais devrait tout de même donner une pente limite non ? Ce que mon équation signifie, c'est que dès que la pente n'est plus nulle, même 0,001% les deux cyclistes avancent à la même vitesse pour tout α alors qu'il y aurait bien une différence sur le plat parfait.
Malheureusement je ne vois pas mon erreur.
Si vous avez une quelconque idée, je suis preneur.
Bonne soirée.
-----