Force de réaction d'un système à trois appuis

[Spacefrogman]

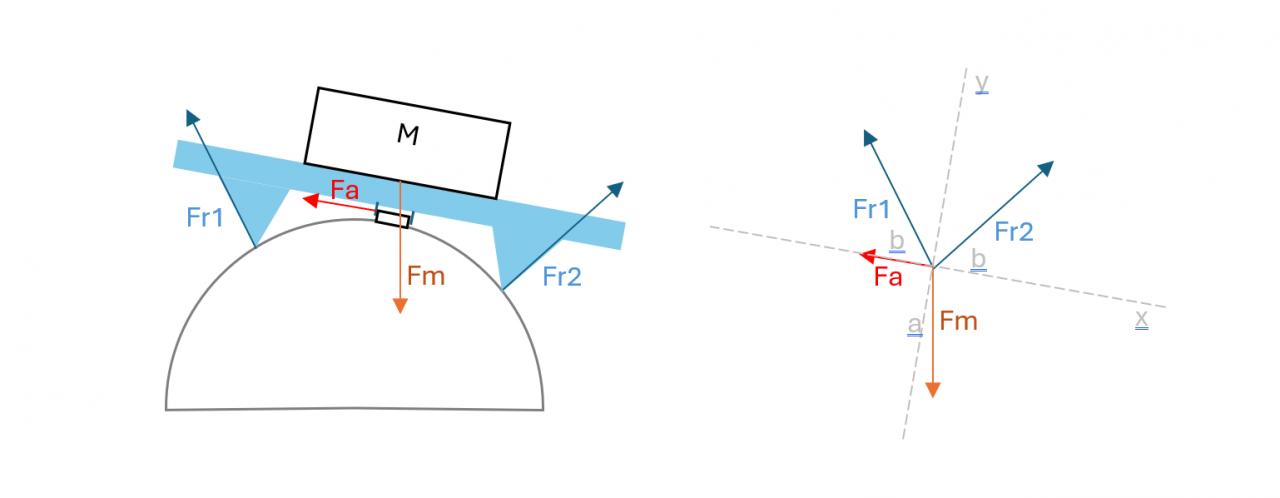
Bonjour, je cherche à déterminer la force de réaction d'un système ayant trois appuis comme le montre la PJ.



Le système étant à l'équilibre, le but ici est de déterminer Fa. Je connais Fm, l'angle a et l'angle b. Cependant, je ne connais pas les forces Fr1 et Fr2 (en sachant que Fr1 et Fr2 ne sont pas perpendiculaires).
J'ai posé mon problème avec mon système d'équations qui n'est composé que de deux équations. Or ici j'ai trois inconnues...
Est-il possible de résoudre ce problème ?

Merci d'avance.
-----

[XK150]

Salut ,

Quel est l'énoncé complet qui conduit à cette figure incomplète ?

Vous parler " d'appuis " sans préciser : pourquoi ? Ce ne peut pas être 3 points alignés , donc ce sont des lignes de contact ???

Tel que dessiné , le système est hyperstatique : si la table bleue est inclinée ( sans glisser ) vers la droite , la force poids se répartit entre l'appui central et celui de droite ( Fr2 ) . Car la force poids passe entre les 2 : telle que dessinée . .
Pourquoi l'appui central de cette forme ????
Dans ces conditions , vous pouvez supprimer l'appui gauche ( Fr 1 ) : il ne sert à rien .

[Black Jack 2]

Bonjour,

Si la boule a un coefficient de frottement nul (avec les pieds bleus), les lignes de forces de Fr1 et Fr2 passent par le centre de la boule (enfin de la demi boule)

Ton dessin n'a que 2 axes (x et y), alors soucis, probable de glissement dans la direction z non indiquée.

Sans tenir compte de cela (et pourtant il faudrait) :

Il faut que la somme des moments des forces par rapport au centre (de la boule) soit nulle.

On peut donc calculer Fa (en connaissant Fm et la géométrie du montage, ses dimensions)

On a alors Fa et Fm connus (amplitude, sens et direction).

On fait graphiquement la somme vectorielle des 4 forces en connaissant les directions et sens de Fr1 et Fr2 ... leurs amplitudes se trouveront en "fermant" la somme vectorielle graphiquement.

Si le dispositif est en 3 dimensions (les 2 indiquées plus celle oubliée (z)), on fait le même chose mais pour que la somme des moments des forces par rapport au centre (de la boule) soit nul, il faut décomposer les forces dans les 3 directions...

[Spacefrogman]

Bonjour,

Je pensais que la figure en 2D suffisait à exprimer mon problème mais si vous voulez je vous montre exactement ce que je veux.
Voici un visu de l'appareil en question :
Capture d'écran 2024-01-05 091304.png

Le système est le suivant :
Un plateau à roulettes est posé sur une coupole et un moteur permet d'entrainer le plateau par un axe situé au centre. Un vérin permet de modifier l'amplitude de la rotation (d'incliner le plateau sur la coupole).
Le but de la manœuvre est de placer des capteurs autour de l'axe centrale. Je souhaiterai donc connaitre la force max appliquée pour dimensionner mes capteurs.

Capture d'écran 2024-01-05 085455.png

Sous le plateau :
Capture d'écran 2024-01-05 085323.png

(Pour des raisons de confidentialité (même si c'est breveté) j'ai dû épurer mon dessin mais en gros il y a un système sous le plateau qui permet de l'entrainer à l'aide d'un axe (partie verte de la dernière capture) glissé dans la bague rouge)

Merci encore.

[A voir en vidéo sur Futura]

[XK150]

Re ,

Pas vraiment compétent , mais j'aime bien comprendre ...

6 roulettes = système hyperstatique : 3 de trop pour les calculs .
Comment le plateau peut il tourner alors qu'il est lié à la coupole rouge par son système d'inclinaison ?
Combien , comment et disposition des capteurs ? A quoi servent ils exactement ?
Donc le plateau n'est pas lié rigidement à son axe ?

[le_STI]

Salut,

Etant donné le système étudié, tu pourrais représenter la liaison [roulettes/sphère] par une liaison rotule centrée au centre de ta sphère.

On en arrive alors à une résolution proche de celle proposée par Black Jack 2, ce qui est cohérent.

Par contre il se pourrait que la solution roues folles + sphère ne fonctionne pas comme prévu.
A ta place j'utiliserais plutôt des roues folles à bille.

[Spacefrogman]

Voici une petite vidéo pour comprendre le principe de l'appareil :
https://www.youtube.com/watch?v=qSC_kp-U9Ks

[sh42]

Bonjour,

Pour moi, ce qui va poser de gros problèmes, ce sont les roulettes orientables car pour changer la direction de ces roulettes, les efforts sont assez conséquents. Dans ce cas les supports à bille sont à mon point de vue préférable car une bille tourne dans tous les sens sans créer de couple par rapport à un axe comme le fait une roulette articulée.
Le défaut des supports à bille est le coefficient de frottement entre la bille et sa surface de portée. A la limite la bille ne tourne plus, ce qui pose un problème.

[Spacefrogman]

Bonjour,

Merci pour vos réponses.
Le principe même de fonctionnement de l'appareil ne peut malheureusement pas être modifié. L'idée des billes est bonne mais mes prédécesseurs ont fait des expériences et en ont conclu qu'elles généraient trop de nuisances sonores et étaient moins solides dans le temps. C'est pourquoi il a été décidé de partir sur l'option des roues pivotantes.

Pour ce qui est de la relation des vecteurs que Black Jack 2 a évoquée, l'idée, si je comprends bien, est de faire quelque chose comme ceci :

Capture d'écran 2024-01-08 113541.png

Et de la, en déduire la "longueur" de chaque flèche (je ne suis pas mécanicien à la base...) ?
Cependant, la flèche que décrit Fr2 peut translater entre la base de Fm et le sommet de Fa.
En gros comme ceci :
Soit : Capture d'écran 2024-01-08 114913.png, soit :Capture d'écran 2024-01-08 114931.png

Comment savoir où placer ce vecteur ? d'autant plus qu'il y a une petite subtilité : la charge sur le plateau se déplace (elle peut être au centre ou au bord du plateau)...
Instinctivement je me dis que si elle est au centre, la masse est répartie quasi équitablement sur les 2 roues, mais si elle est au bord gauche, par exemple, c'est la roue de gauche que va prendre presque toute la charge.

Y a-t-il une relation permettant de déterminer cela ? Une histoire de couple j'imagine ?

Merci.

[Black Jack 2]

Rebonjour,

Dans le modèle simplifié à 2 dimensions ...

M*g est connu, d est connu.
La distance "a" est calculable pour chaque position de la "table" sur la demi boule.

On peut donc calculer Fa (comme expliqué dans ma première intervention)

On connait donc, pour une position donnée, les amplitudes, directions et sens de M.g et de Fa ... et on connait les directions de Fr1 et Fr2, on peut alors "fermer" le dessin des forces vectorielles et par là calculer les valeurs de Fr1 et Fr2.

Voir la remarque de mon message précédent avec un système en 3 dimensions.

[sh42]

Bonjour,

Il y a un vice dans le raisonnement du fait qu'en théorie si l'on admet que le plateau est rigide, il ne peut y avoir 3 points de portage. s'ajoute à cela que l'on admet une force Fa tangente au point de contact A, ce qui est contraire à la loi qui veut que sans frottement la force est perpendiculaire à la surface tangente à celles du point d'appui.

Si l'on admet que des points de contact sont des liaisons élastiques ou que le plateau est souple, là effectivement, il peut y avoir 3 points de portage.

[Black Jack 2]

"s'ajoute à cela que l'on admet une force Fa tangente au point de contact A, ce qui est contraire à la loi qui veut que sans frottement la force est perpendiculaire à la surface tangente à celles du point d'appui."

Bonjour,

Pas vraiment, il y a des petits "rebords" qui permettent d'avoir Fa "tangent".

Voir sur le zoom, les petits rebords sont pointés par les flèches mauves.

Le rectangle noir est solidaire de la demi boule (sur laquelle il peut se mouvoir) et les petits rebords sont solidaires de la table bleue.

[sh42]

Bonsoir,

Je n'avais pas remarqué ce détail.

Le plateau n'est donc supporté que par Fr1 et Fr2 et effectivement Fa est la somme vectorielle de Fr1, Fr2 et M.
Effectivement vu la conception, le point A ne reprend aucune charge verticale.

[le_STI]

M*g est connu, d est connu.
La distance "a" est calculable pour chaque position de la "table" sur la demi boule.

On peut donc calculer Fa (comme expliqué dans ma première intervention) .....

... et la résolution peut s'arrêter là puisque Spacefrogman voulait calculer Fa