Transformations de Lorentz

[Geo77b]

Bonjour,
On a donc une source lumineuse en mouvement qui émet à t=0, un front d'onde sphérique (symétrique) dans son référentiel, et on peut calculer la forme de ce front d'onde vu dans un référentiel fixe. Cette forme doit être sphérique également.
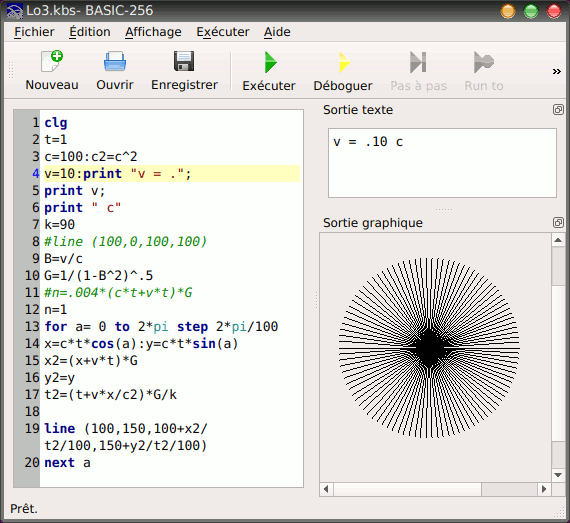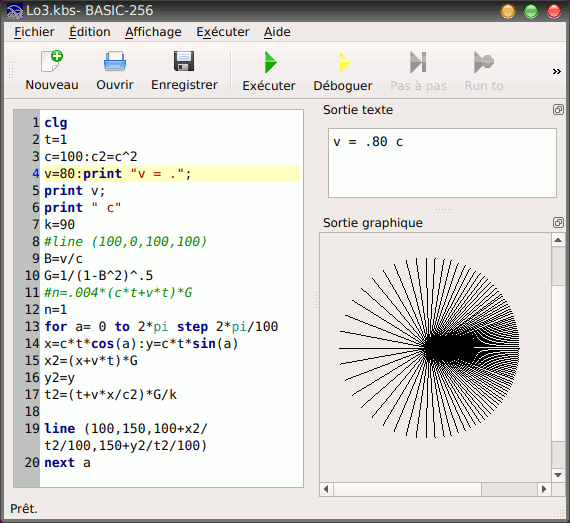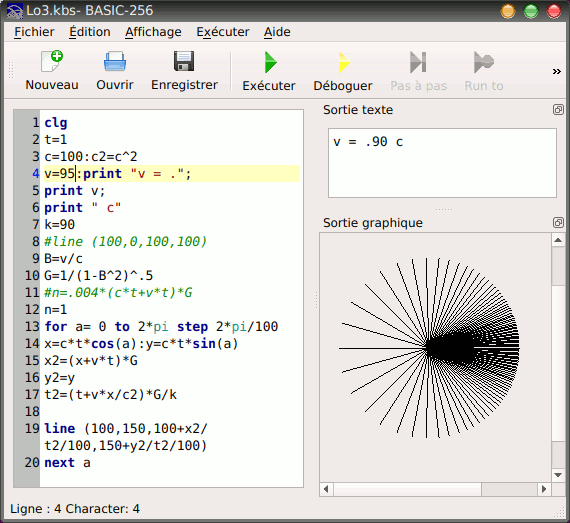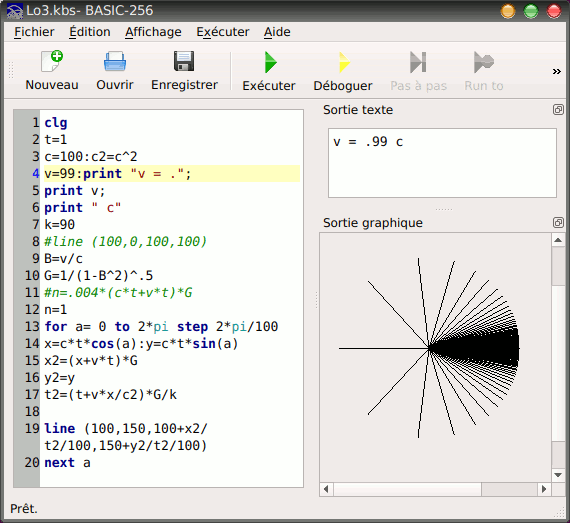
Après calcul, je trouve bien un front d'onde sphérique, mais pas symétrique (voir image ci-dessous). Est-ce correct ? Comment interpréter cette dissymétrie ? La luminosité varie-t-elle suivant qu'on regarde la source s'éloigner ou se rapprocher ?
Merci.



-----

[La Limule]

Regarde la définition d'un front d'onde
https://fr.wikipedia.org/wiki/Front_...radio%2C%20etc.).
Pour un observateur à un instant donné c'est un ensemble de points ayant une meme phase.
Supponsons qu'on aie une souce sonore . dans son référentiel il y a une symétria sphérique
et maintenant penons la meme source en mouvement . que vont entendre a un instant t deux observateurs , l'un devant
la source sonore qui s'approche et l'autre qui la voit s'éloinger?
L'effet Doppler Fizeau est connu . ils ne perecevront pas la meme fréquence. les phases toutneron différemment.
Bon c'est quantitatif. et pose déja probleme bien avant des vitesses relativistes....
gts2 pourrait sans doute nous dire ce que devient un front d'onde d'une source en mouvement.

[coussin]

Je ne suis pas sûr de ce que représente la figure du message #1 mais, oui pour des vitesses relativistes on perd la "symétrie sphérique" simplement par effet Doppler. Voir la figure 1 de la page wikipédia https://en.wikipedia.org/wiki/Relati...Doppler_effect

[Geo77b]

Merci pour les réponses.
Il ne s'agit pas ici de phase ou de fréquence ou de Doppler.
Je reprend la présentation du "Berkeley" (voir ci-dessous). La source émet un flash dans un référentiel en mouvement, flash représenté par des lignes (trajectoires de photons) dans toutes les directions (uniformément), et je calcule ce que deviennent ces trajectoires dans un autre référentiel (fixe), avec les formules de Lorentz.

Sur la figure 1, je représente les trajectoires calculées (en faisant varier pour chaque image la vitese v de la source de 0,1 c à à,99 c) , qui sont plus concentrées d'un côté que de l'autre, donc plus de photon au m², .
Il s'agit donc ici de "densité" de photons, et non pas du temps perçus entre l'arrivée de deux cycles successifs.

[A voir en vidéo sur Futura]

[ThM55]

Bonjour. C'est un effet dû à la transformation des vitesses dans les transformations de Lorentz.

Le front d'onde doit rester sphérique si on est dans un référentiel où la source est en mouvement car la vitesse de la lumière dans le vide est toujours c pour cet observateur.

Cependant, le vecteur vitesse n'est pas un invariant. En prenant les quotients des différentielles des TL pour un boost le long de l'axe Ox, on trouve la loi bien connue de composition des vitesses mais aussi que les composantes transverses sont modifiées (contrairement aux coordonnées transverses):







C'est bien sûr une conséquence de la transformation de t. Il en résulte que la direction d'un rayon lumineux apparaîtra différente dans le référentiel de l'observateur.

Par exemple si et on voit qu'on a:



(Ici, ). On voit que l'angle n'est pas le même dans les deux référentiels.

Dans le cas ultrarelativiste pour une particule de masse non nulle, on fait et cette relation devient



C'est aussi valable pour un rayon lumineux à vitesse c.

Je vais considérer deux cas numériques avec V = 4c/5, pour lequel :

1) (donc un rayon allant vers la droite avec un angle de 45°; sinus et cosinus sont



L'angle dans le référentiel transformé est de 15 degrés.

2) (le rayon va vers la gauche avec un angle de 45°; le cosinus est négatif).



Cette fois l'angle est de 77°.

Donc les rayons lumineux de la source en mouvement apparaissent bien focalisés vers l'avant, et plus dilués vers l'arrière. Je crois que c'est ce que vous observez dans votre simulation. Et j'ajouterais que vous méritez des félicitations pour avoir mis cela en évidence!

[Geo77b]

Merci.
Dilués vers l'arrière, cela voudrait-il bien dire que la source paraîtrait moins lumineuse quand elle s'éloigne (étoiles lointaines)?
J'imagine que c'est trop faible pour avoir été vérifié expérimentalement.
A la sortie du prisme d'un spectromètre, on a une source quasi ponctuelle dont les rayons partent avec un angle différent suivant la "couleur". Ces angles seraient-ils modifiés/dilués avec la vitesse ?
Merci.

[gts2]

Bonjour,

La loi de transformation de ces angles est celle donnée au message #5.

[Geo77b]

Merci.
Dans ce cas, plutôt que de mesurer une variation de luminosité, il serait peut-être plus facile de mesurer une variation d'angle.

[La Limule]

Que deviennent les formules si la source émet des particules de masse non nulle ? (j'avais écrit que le problème devait déja se poser
avec des ondes sonores)

[gts2]

De quelles formules parlez-vous ? S'il s'agit de l'angle, elles sont données par @ThM55 dans le message #5.

[ThM55]

NB: la première formule pour la tangente s'applique à toute particule, pas seulement de masse nulle.

Petit exercice facile: quel est l'angle obtus le plus grand dans le référentiel de l'émetteur qui devient aigu ou droit dans celui de l'observateur?

Si les angles sont modifiés comme je l'ai indiqué, il est clair que l'intensité est concentrée vers l'avant et réduite vers l'arrière.

Une application bien connue et très utile est le rayonnement synchrotron.

Petite digression préalable: le synchrotron est un appareil relativiste: il remplace le cyclotron qui devient inefficace au dessus d'une certaine vitesse parce qu'on ne peut plus synchroniser le champ accélérateur avec la rotation des électrons à cause de la dilatation du temps.

La rayonnement synchrotron est produit par les électrons accélérés dans un synchrotron (le top c'est l'ESRF à Grenoble: https://www.esrf.fr/ ). Ce rayonnement possède des caractéristiques remarquables: très large large spectre, pulsé, etc., qui facilitent un grand nombre d'applications, notamment dans le domaine des rayons X. Une des caractéristiques appréciables est qu'il est de très grande luminosité justement grâce à cet effet de focalisation vers l'avant dû aux transformations de Lorentz.

[ThM55]

Merci.
J'imagine que c'est trop faible pour avoir été vérifié expérimentalement.
Merci.

De ces formules on peut tirer un effet curieux: la vitesse apparente v' (projetée sur le ciel) d'une source astronomique lumineuse qui se déplace avec une vitesse v le long d'une direction qui fait un certain angle avec la ligne de visée peut être mesurée comme plus grande que c. C'est un effet de perspective, ce n'est pas réel (on a bien évidemment v<c). Je me souviens avoir vu des observations de cet effet. Je n'ai plus les références mais si des connaisseurs en astronomie les ont, ils pourraient compléter ce message.

[La Limule]

Dans ma premiere réponse (post 2) je signalais que l'effet Doppler meme non relativiste était un début d'explication
a l'asymétrie qu'il ne s'expliquait pas.
si la source qui est sur un train allant a une vitesse V dépasse la gare et veut lui envoyer une particule ca va dépendre de
l'énergie fournie pour qu'elle aille vraiment vers la gare et pour toute énergie inférieure meme lancée vers l'arriere,
ca ira vers l'avant.
C'est bien connu mais on voit que la problématique est prérelativiste.

[Calvert]

Je n'ai plus les références mais si des connaisseurs en astronomie les ont, ils pourraient compléter ce message.

C'est un phénomène relativement commun aux objets qui émettent des jets relativistes. Voir par exemple ceci comme introduction.

[Geo77b]

quel est l'angle obtus le plus grand dans le référentiel de l'émetteur qui devient aigu ou droit dans celui de l'observateur?

Pour (cosθ'+v/c)=0

Si les angles sont modifiés comme je l'ai indiqué, il est clair que l'intensité est concentrée vers l'avant et réduite vers l'arrière.

J'ai lu qu'on calculait la distance des étoiles lointaines à partir de la luminosité des étoiles variables, et leur vitesse d’éloignement serait d’autant plus grande qu’elles sont éloignées.

C'est un phénomène relativement commun aux objets qui émettent des jets relativistes. Voir par exemple ceci comme introduction.

Si je comprend bien, l'erreur serait due au fait que le jet n'est pas ponctuel.

[ThM55]

J'ai lu qu'on calculait la distance des étoiles lointaines à partir de la luminosité des étoiles variables, et leur vitesse d’éloignement serait d’autant plus grande qu’elles sont éloignées.

Non, les étoiles variables n'ont pas une vitesse d'éloignement d'autant plus grande qu'elles sont plus éloignées. Ça c'est pour les galaxies assez éloignées. Mais il est exact qu'on mesure la distance de certaines étoiles variables périodiques appelées "céphéides" à partir de leur luminosité apparente et cela est rendu possible par le fait qu'il existe une relation liant la période et la luminosité absolue (voir https://fr.wikipedia.org/wiki/C%C3%A9ph%C3%A9ide ). Mais aucun rapport avec la question.

[Geo77b]

Mais aucun rapport avec la question.

Dans le même wiki, on dit :

Très brillantes, donc visibles de loin, les céphéides sont détectées à présent dans d'autres galaxies que la nôtre, jusqu'à des distances de 80 millions d'années-lumière environ grâce au télescope spatial Hubble. Ces déterminations de distances sont essentielles au calcul de la valeur de la constante de Hubble, qui mesure le rythme d'expansion de l'Univers.

J'avais aussi lu ceci :
https://www.20minutes.fr/sciences/33...vers-expansion

Le rapport serait qu'on se sert de la mesure de la luminosité pour calculer les distances et la constante de Hubble, et que la mesure de la luminosité pourrait être affectée par la vitesse d'éloignement.

[ThM55]

D'accord, je comprends mieux ce que vous voulez dire.

Si la source lumineuse est isotrope dans son référentiel de repos, alors dans un espace euclidien statique l'énergie sera répartie uniformément sur une sphère dont le diamètre est la distance de l'observateur. Dans un espace en expansion, c'est différent. On tient compte de facteurs dépendant de l'expansion, de la perte d'énergie des photons due au red-shift , etc. et on définit une "distance de luminosité" différente.

J'avoue que j'ai largement oublié les détails et les calculs car cela fait des années que je n'ai plus fait de cosmologie. Mais ma première intuition est que dans l'hypothèse où les galaxies sont "au repos" dans le référentiel en comouvement de la métrique de Friedman-Lemaître, il n'y aura pas un effet tel que celui impliqué par la transformation de Lorentz pour les vitesses. On aurait certainement un effet de ce type s'il y avait un mouvement particulier d'une galaxie, une vitesse par rapport au référentiel de comouvement. Ce serait une chose à vérifier avec les équations du modèle. Si je me trompe, alors ce serait une nouveauté, il faudrait corriger la plupart des traités de cosmologie, donc j'en doute fort.