hello
je me penche sur la section Effets_théoriques_sur_la_Terre ### article mis à jour depuis, voir https://forums.futura-sciences.com/p...ml#post7281010 pour un lien vers la version de l'article contemporaine du début de ce fil ###
on y lit que les résultats "attendus" (on n'ira pas vérifier!) divergent: le centre de la Terre pourrait être plus jeune ou plus vieux
Qu'en est-il?
Sinon, on pourrait couper la Terre dans les trois directions, le centre est alors à la surface des 8morceaux obtenus. Les morceaux ne sont pas sphériques mais on peut approximer chaque morceau par des boules, une grosse (tangente aux côté d'un tétraèdre, centre situé aux 3/4 du sommet) et des petites (idem tangentes aux tétraèdres) pour représenter les portions restantes, la précision du résultat dépendant du nombre de boules considérées. Ce calcul a-t-il déjà été effectué?
Le calcul me parait faisable (que fait-on des dilatations obtenues pour chaque boule, on les ajoute?) mais du coup je ne comprends pas ce qui peut créer un paradoxe, à priori avec un tel calcul, on doit pouvoir trancher si le centre de la Terre est plus jeune ou plus vieux. J'ai loupé quelque chose?
-----



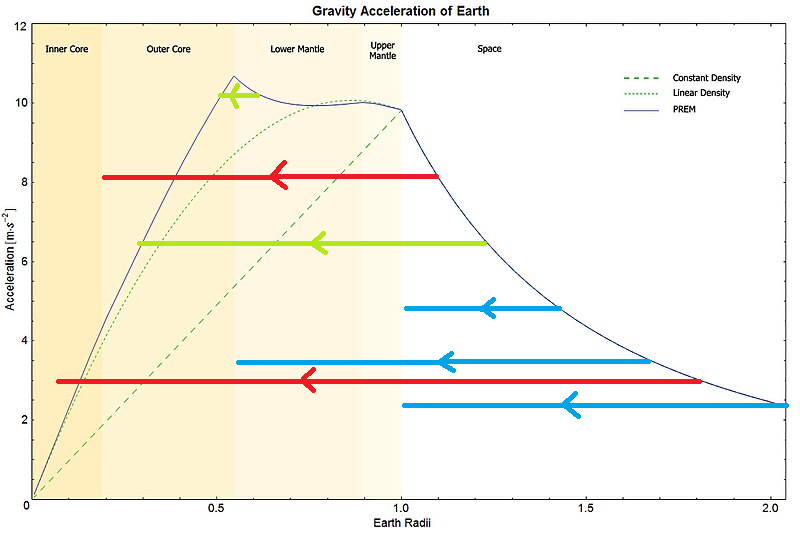
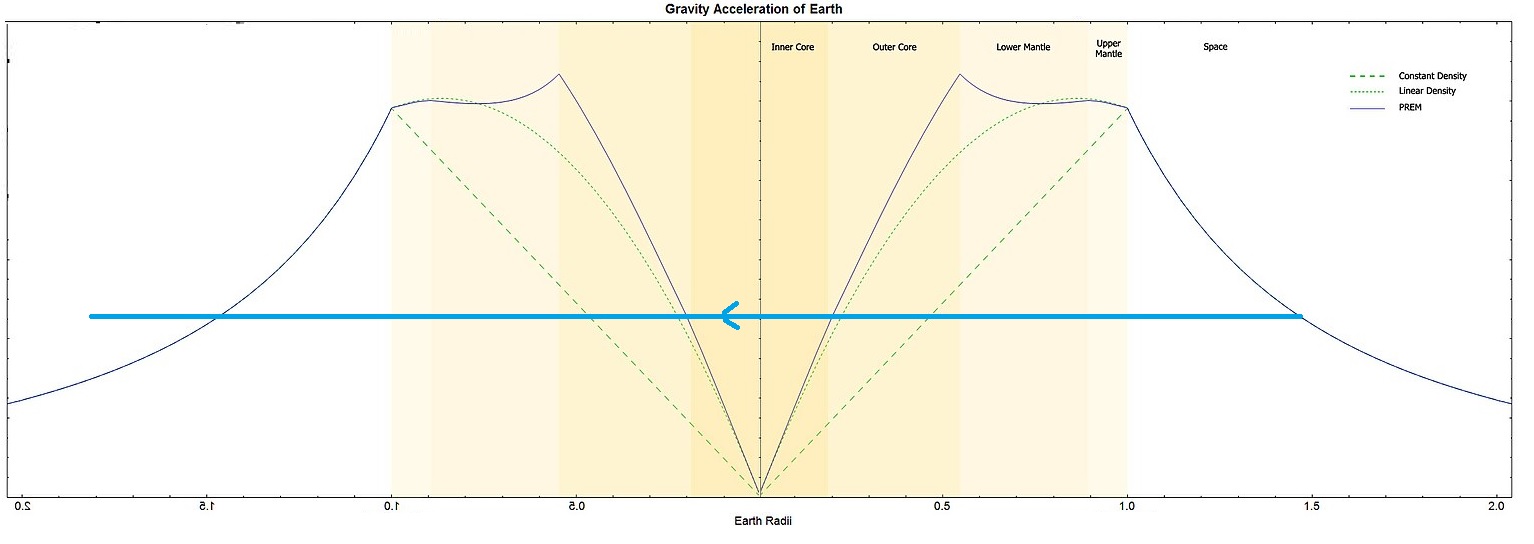
 (avec A<0)
(avec A<0)