Champ de vitesse autour d'un cylindre

[Virginie013]

Bonjour à tous,

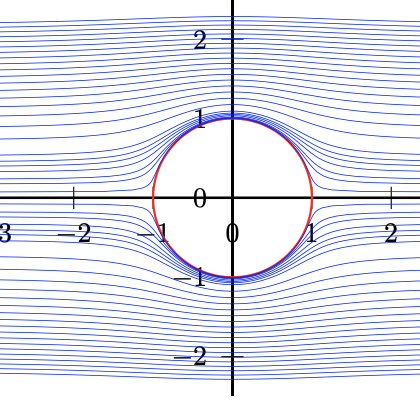
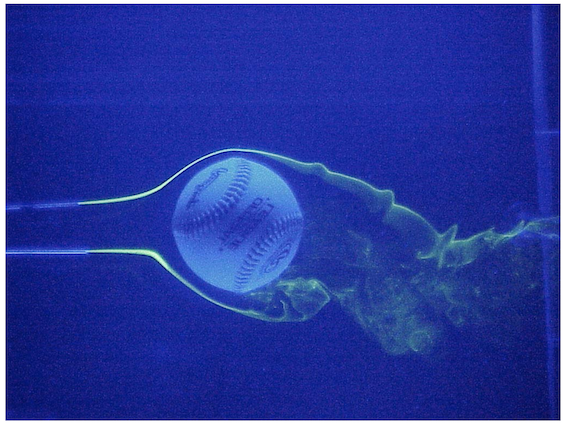
Concernant le champ de vitesse dans un fluide qui s'écoule autour d'un cylindre de rayon a qui tourne autour de son axe à la vitesse angulaire Ω. La vitesse du fluide loin du cylindre est notée U0.

Dans la capture d'écran jointe, il est écrit que la vitesse du fluide à la surface du cylindre est égale à la vitesse de rotation du cylindre soir aΩ. Cependant, quand on regarde l'expression du champ de vitesse, on voit qu'en r = a (à la surface du cylindre), la vitesse n'est pas égale à aΩ puisqu'on a ||v(a,θ)|| = |- 2 U0 sin(θ) + Γ/2πa|.

Comment est-ce possible ?

Supposons maintenant que le cylindre soit fixe (Ω = 0 et Γ = 0), on trouve ||v(a,θ)|| = 2 U0 |sin(θ)|.

En haut du cylindre (θ = π/2), on trouve donc v = 2 U0.

Comment est-ce possible que la vitesse soit deux fois plus grande que la vitesse de l'écoulement ?


-----

[gts2]

Bonjour,

La vitesse du fluide à la surface du cylindre ne vaut pas aΩ

Pour ce qui est de la vitesse double, le problème considéré est un écoulement "incompressible" donc le débit volumique se conserve et pour "éviter" le cylindre, on voit bien qu'il faut que les lignes de courant se resserrent et que la vitesse augmente.

[Virginie013]

Bonjour

Merci pour votre réponse.

Il y a donc une erreur dans ce qui est écrit ?

Effectivement , je n'avais pas pris en compte la conservation du débit volumique.

Si le fluide est réel et qu'on tient compte de sa viscosité, la condition d'adhérence impose que la vitesse du fluide à la surface du cylindre immobile soit nulle (ou aΩ si le cylindre est en rotation) et pourtant on a quand même conservation du débit volumique et le fluide doit toujours "éviter" le cylindre.

Donc pourquoi dans le modèle de fluide parfait on a 2 U0 à la surface du cylindre alors que dans le modèle avec viscosité cette vitesse est bien nulle ?

J'aurai tendance à dire que dans le modèle du fluide réel, les couches de fluide vont être entraînées les unes avec les autres ce qui autorise à ce que la vitesse soit différente est plus faible à la surface du cylindre. Alors que dans le modèle du fluide parfait où les couches de fluide sont indépendantes, il faut mettre le paquet à la surface du cylindre ce qui donne une vitesse non nulle.

Existe-t-il un modèle avec un écoulement parfait mais dans lequel on impose dans les conditions aux limites une condition d'adhérence au niveau de la surface du cylindre ? Même si l'écoulement est parfait, on peut quand même dire que la couche limite visqueuse permet à ce que la vitesse du fluide sur le cylindre soit égale à la vitesse du cylindre non ? Cela ne pourrait-il pas améliorer le modèle précédent qui me paraît un peu limite...? Dans ce modèle, j'ai l'impression qu'on impose seulement à ce que la composante normale de la vitesse du fluide soit nulle sur le cylindre...

V

[gts2]

Si le fluide est réel et qu'on tient compte de sa viscosité, la condition d'adhérence impose que la vitesse du fluide à la surface du cylindre immobile soit nulle (ou aΩ si le cylindre est en rotation) et pourtant on a quand même conservation du débit volumique et le fluide doit toujours "éviter" le cylindre.

Le aΩ c'est à la surface du cylindre, cela n'empêche pas, lorsqu'on s'éloigne, que la vitesse devienne plus grande que U0.

Donc pourquoi dans le modèle de fluide parfait on a 2 U0 à la surface du cylindre alors que dans le modèle avec viscosité cette vitesse est bien nulle ?

Réponse brutale dans le cas du cylindre, vous êtes en train d'étudier l'écoulement de l'eau sèche (formule de Feynman) donc sans réalité physique.
Réponse dans le cas d'un corps profilé, il y a une zone de transition d'épaisseur faible (couche limite), dans laquelle on passe de v=0 à la surface à v solution de l'équation fluide parfait lorsqu'on s'éloigne un peu.

Existe-t-il un modèle avec un écoulement parfait mais dans lequel on impose dans les conditions aux limites une condition d'adhérence au niveau de la surface du cylindre ?

Non, au vu de l'équation aux dérivées partielles, les mathématiciens nous disent que pour trouver une solution, on ne peut imposer que la composante normale.

Même si l'écoulement est parfait, on peut quand même dire que la couche limite visqueuse permet à ce que la vitesse du fluide sur le cylindre soit égale à la vitesse du cylindre non ? Cela ne pourrait-il pas améliorer le modèle précédent qui me paraît un peu limite...?

Ce que vous décrivez est le modèle de la couche limite qui ne fonctionne pas pour un cylindre, l'écoulement réel autour d'un cylindre est très différent

Dans ce modèle, j'ai l'impression qu'on impose seulement à ce que la composante normale de la vitesse du fluide soit nulle sur le cylindre...

C'est bien le cas et c'est ce que les mathématiciens nous disent : on ne peut rien imposer de plus.
Rappel : ne pas oublier que vous êtes en train d'étudier l'eau sèche.

[A voir en vidéo sur Futura]

[Virginie013]

Merci pour votre réponse.

Je m'interroge sur un autre point.

Si on tient compte de la viscosité du fluide, la valeur de la vitesse du fluide sur le cylindre devrait être la même partout (RΩ) en raison de la condition d'adhérence. Dans ce cas comment expliquer l'effet Magnus (qui provient justement de la différence de vitesses et donc de pression entre deux points du cylindre) ? Existe-t-il un modèle "simple" pour exprimer la force de Magnus sur un cylindre ou une sphère en tenant compte de la viscosité du fluide (pour un certain nombre de Reynolds où cela est possible) ?

V

[gts2]

Il y a plusieurs possibilités de réponse :

idéalisé : couche limite de faible épaisseur permettant de passer de RΩ au champ de vitesse de votre premier message, mais je ne suis pas sûr de trouver des études le justifiant

réalité : les lignes de courant (cas d'une balle de base-ball) ressemble plutôt à cela :



Et l'effet Magnus vient de la position du décollement de la couche limite qui dépend de la vitesse de la balle.

Je ne suis pas sûr qu'il y ait un cas réel correspondant à votre cas idéalisé : il faudrait voir du côté des voiles de Flettner et son évolution avec aspiration qui font peut-être un contrôle suffisamment fin de la couche limite.
Mais je n'ai jamais vu de tracé de lignes de courant réel de ces voiles.

[harmoniciste]

Si on tient compte de la viscosité du fluide, la valeur de la vitesse du fluide sur le cylindre devrait être la même partout (RΩ) en raison de la condition d'adhérence. Dans ce cas comment expliquer l'effet Magnus (qui provient justement de la différence de vitesses et donc de pression entre deux points du cylindre) ?

Bonjour,
Oui, la vitesse du fluide au contact du cylindre est la même partout. Mais en raison de la transmission des pressions par le fluide, c'est l'ensemble des vitesses au voisinage du cylindre (pas seulement "au contact") qui est responsable du champ de pression sur la surface.
Il en est d'ailleurs de même pour un profil d'aile, au contact duquel la vitesse du fluide est nulle en tout point. Ce qui n'empêche évidemment pas de constater l'existence de pressions variées à sa surface.