Bonjour à tous,
J'aimerais modéliser le rayonnement acoustique d'un double vitrage d'après la thèse de O. Kaiser. Il utilise une transformée de Fourier spatiale pour définir une matrice de rayonnement M (équation 4.122),
et trace à la figure 4.9 les contributions modales données par plusieurs modes de vibration d'une plaque seule.
J'ai des difficultés à coder cette équation, je ne parviens pas à retrouver le même type de courbes.
Voilà mon code à l'heure actuelle :
La courbe que j'obtiens en sortie de ce code ne correspond pas à ce que je devrais trouver d'après la thèse...Code:clear all, close all rho0 = 1.29; % masse volumique de l'air (kg/m^3) c = 340; % célérité du son dans l'air (m/s) p0 = 2e-5; % pression de référence (Pa) %% paramètres temporels fs = 2048; % fréquence d'échantillonnage (Hz) L_signal_tmp = 1000; % longueur du signal NFFT = 2^nextpow2(L_signal_tmp); % nombre de points de la fft t = (1:L_signal_tmp)/fs;% vecteur temps (s) f = fs/2*linspace(0,1,NFFT/2+1); % vecteur fréquence (Hz) w = 2*pi*f; % vecteur fréquenec (rad/s) %% indices modes de la plaque m = [1 1 2 2 3 3 4 3 1]'; n = [1 2 1 2 1 2 1 2 3]'; cmn = length(m); %% Dimensions de la plaque Lx = 717e-3;%2455e-3;%1.044;% (m) Ly = 1091e-3;%788e-3;%0.667;% (m) %% paramètres spatiaux % longueur des signaux L_signal_x = 50; L_signal_y = 70; % nombres de points des fft nfftx = 2^nextpow2(L_signal_x); nffty = 2^nextpow2(L_signal_y); % période spatiale Dx = Lx/(L_signal_x-1); Dy = Ly/(L_signal_y-1); % vecteurs espace x = (1:L_signal_x)*Dx;%% y = (1:L_signal_y)*Dy;%% % incréments spatiaux dx = x(2)-x(1); dy = y(2)-y(1); % vecteur des nombres d'ondes K=w/c; kx = 2*pi/(2*Dx)*(1:nfftx/2+1)/(nfftx/2+1);%linspace(0,1,nfftx/2+1); ky = 2*pi/(2*Dy)*(1:nffty/2+1)/(nffty/2+1);%linspace(0,1,nffty/2+1); dkx = kx(2)-kx(1); dky = ky(2)-ky(1); %% déformée de la plaque Phi_mn = zeros(length(x), length(y), length(m)); kxm = m*pi/Lx; kyn = n*pi/Ly; for idx=1:cmn Phi_mn(:,:,idx) = sin(kxm(idx)*x')*sin(kyn(idx)*y); end % PHI_mn2 = fft(fft(Phi_mn,nfftx,1),nffty,2)/L_signal_x/L_signal_y; for idx=1:cmn PHI_mn2(:,:,idx) = fft2(Phi_mn(:,:,idx))/L_signal_x/L_signal_y; end PHI_mn = PHI_mn2(1:nfftx/2+1, 1:nffty/2+1, :); % sa fft %% calcul de la matrice de rayonnement M=zeros(cmn,cmn,length(w)); for kk=1:length(K) integrale = zeros(cmn); for ix = 1:nfftx/2+1 for iy = 1:nffty/2+1 integrale = integrale + conj(squeeze(PHI_mn(ix,iy,:)))*squeeze(PHI_mn(ix,iy,:)).'/sqrt(K(kk)^2-kx(ix)^2-ky(iy)^2); end end M2(:,:,kk) = w(kk)*integrale; % M(:,:,kk)=w(kk)*M2(:,:)./kz2(kk);%PUISSANCE(kk) = v1_mn(:,kk)'*M(:,:,kk)*v1_mn(:,kk); end M = rho0./(8*pi^2)*real(M2)*dkx*dky; % semilogx(f,20*log10(abs(PUISSANCE(1,:))/Puiss_ref)) % surf(ky,kx,PHI_mn(:,:,1)) semilogx(f,20*log10(abs(squeeze(M(1,1,:))))) xlabel('Frequency (Hz)'), ylabel('Amplitude (dB)'); % semilogx(f,(abs(squeeze(M(1,1,:)))))
Si quelqu'un a un peu de temps à consacrer pour regarder ça, je lui en serai très reconnaissant.
-----




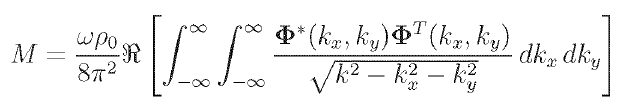
 se répète 2 fois.
se répète 2 fois.
