Bonjour
J'ai reproduis quelques fonctions de la classe math.h en langage C, pour essayer de comprendre comment cela fonctionnait, mais j'aimerais optimiser mes fonctions et surtout rendre ma fonction tan, arcsin, arccos et arctan plus précise sur certaines valeur, je m'explique:
Voila mon approximation de sin (précise sur toutes valeurs):
Mon approximation de cos (précise sur toutes valeurs):Code:alpha = angle * 0.0174532925199432; alpha2 = alpha * alpha; alpha3 = alpha2 * alpha; alpha5 = alpha2 * alpha3; sinus = alpha - (0.1666666666666666 * alpha3) + (0.0083333333333333 * alpha5) - (0.0001984126984126 * (alpha5 * alpha2));
Une fois dans des fonctions, ces calculs s’exécutent aussi rapidement que celles de math.h, donc c'est très bienCode:alpha = angle * 0.0174532925199432; alpha2 = alpha * alpha; alpha4 = alpha2 * alpha2; cosinus = 1.0 - ((0.5 * alpha2) - (0.0416666666666666 * alpha4) + (0.0013888888888888 * (alpha2 * alpha4)) - (0.0000248015873015 * (alpha4 * alpha4)));
On serait tenté pour calculer tan, d'écrire:
C'est bien mais ça prend un peu moins du double de temps à calculer par rapport à math.h, donc j'ai cherché sur wikipedia (ou autre), et j'ai trouvé ceci:Code:sinus / cosinus
Explication:Code:alpha = angle * 0.0174532925199432; tangente = alpha + ((0.3333333333333333 * (alpha * alpha * alpha)) + (0.1333333333333333 * (alpha * alpha * alpha * alpha * alpha)) + (0.0539682539682539 * (alpha * alpha * alpha * alpha * alpha * alpha * alpha)));
La c'est très très rapide à calculer, sauf que pour des valeurs d'angle supérieurs à 45 degrés, les résultats se dégradent très rapidement en précision car il faut de plus en plus d'itérations (fonction infinie) pour obtenir une précision acceptable.
Normalement on parle de séries de Taylor, pour sinus on voit qu'il faut très peut d'itérations pour avoir une précision assez grande (pour de la robotique), de même que cosinus, par contre ce n'est pas du tout le cas pour tangente.
Pour sinus et cosinus le calcul converge, il est constitué de - + - + - etc..., par contre pour calculer tangente ce sont des + + + +.
Je veux bien calculer tangente avec une division de sinus / cosinus, elle prend environ 200 micro seconde de plus que math.h, c'est pas trop grave. Par contre le soucis est le même pour arcsin, arccos, et arctan.
Jusqu'à aujourd'hui je calculais arcsin, arccos, et arctan en faisant des "tests" de différentes valeurs de sinus, cosinus, et tangente, ça marche bien, mais niveau temps de calcul on entre dans plusieurs milli (pas micro) secondes. Donc quand on veut faire un algorithme qui réagit dans la milliseconde on est foutu.
La solution est d'utiliser des séries:
arcsin:
arccos:Code:return (SINUS + ((0.5 * ((SINUS * SINUS * SINUS) * 0.3333333333333333)) + (0.375 * ((SINUS * SINUS * SINUS * SINUS * SINUS) * 0.2)) + (0.3125 * ((SINUS * SINUS * SINUS * SINUS * SINUS * SINUS * SINUS) * 0.1428571428571428)))) * _RADIAN_TO_DEGREE;
arctan:Code:return (1.5707963267948966 - (COSINUS + ((0.5 * ((COSINUS * COSINUS * COSINUS) * 0.3333333333333333)) + (0.375 * ((COSINUS * COSINUS * COSINUS * COSINUS * COSINUS) * 0.2)) + (0.3125 * ((COSINUS * COSINUS * COSINUS * COSINUS * COSINUS * COSINUS * COSINUS) * 0.1428571428571428))))) * _RADIAN_TO_DEGREE;
Mais le phénomène étant bien qu'il faille itérer un grand nombre de fois pour certaines valeurs, pour obtenir une précision acceptable.Code:return (TANGENT - (((TANGENT * TANGENT * TANGENT) * 0.3333333333333333) + ((TANGENT * TANGENT * TANGENT * TANGENT * TANGENT) * 0.2) - ((TANGENT * TANGENT * TANGENT * TANGENT * TANGENT * TANGENT * TANGENT) * 0.1428571428571428))) * _RADIAN_TO_DEGREE;
Auriez vous une idée de comment faire? (mise à part la blague: utilises math.h)
-----



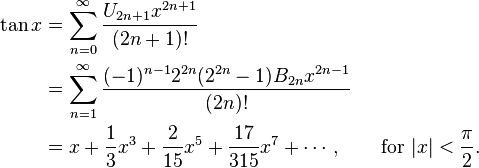

 (pour
(pour 



 )
)